
- •Министерство аграрной политики украины
- •Издание рассмотрено и рекомендовано к печати на заседании кафедры физико-математических дисциплин (протокол № 2 от 9 октября 2007г.);
- •Содержание
- •1. Линейная алгебра
- •1.1. Системы линейных уравнений
- •1.2. Метод обратной матрицы
- •1.3. Метод Крамера
- •1.4. Метод Гаусса
- •1.5. Вопросы для самоконтроля
- •2. Аналитическая геометрия на плоскости
- •2.1. Линии первого порядка
- •2.2. Линии второго порядка Окружность
- •Гипербола
- •Парабола
- •2.3. Вопросы для самоконтроля
- •3. Векторная алгебра
- •3.1. Основные определения и понятия
- •3.2. Скалярное произведение векторов
- •3.3. Векторное произведение векторов
- •3.4. Смешанное произведение векторов
- •3.5. Вопросы для самоконтроля
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость в пространстве
- •4.2. Прямая в пространстве
- •4.3. Прямая и плоскость в пространстве
- •4.4. Вопросы для самоконтроля
- •Литература
- •Индивидуальные задания к расчётно-графической работе Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Для выполнения ргр
- •211 Группа
- •212 Группа
- •213 Группа
- •214 Группа
- •215 Группа
- •311 Группа
- •312 Группа
- •313 Группа
- •314 Группа
- •315 Группа
- •316 Группа
- •1111 Группа
- •1112 Группа
- •1211 Группа
- •1212 Группа
- •1311 Группа
- •1312 Группа
- •1313 Группа
- •1511 Группа
- •1512 Группа
2. Аналитическая геометрия на плоскости
2.1. Линии первого порядка
В декартовых координатах уравнение первой степени определяет некоторую прямую.
Линии, которые в декартовых координатах определяются уравнением первой степени, называются линиями первого порядка. Следовательно, каждая прямая есть линия первого порядка.
Общее уравнение прямой (как общее уравнение первой степени) определяется уравнением вида:
Ах + Ву + С = 0.
Рассмотрим неполные уравнения прямой.
1. С = 0. Уравнение прямой имеет вид: Ах + Ву = 0; прямая проходит через начало координат.
2 .В
= 0 (А
0). Уравнение имеет вид Ах
+ С
= 0 или х
= а,
где а =
.В
= 0 (А
0). Уравнение имеет вид Ах
+ С
= 0 или х
= а,
где а =
![]() Прямая проходит через точкуА(а;
0), она
параллельна оси Оу.
Число а
есть величина отрезка, который отсекает
прямая на оси Ох
(рис. 1).
Прямая проходит через точкуА(а;
0), она
параллельна оси Оу.
Число а
есть величина отрезка, который отсекает
прямая на оси Ох
(рис. 1).
Рис. 1
Если а = 0, то прямая совпадает с осью Оу. Уравнение оси ординат Оу имеет вид: х = 0.
3 .А
= 0 (В
0). Уравнение имеет вид: Ву
+ С
= 0 или у
= b,
где b
=
.А
= 0 (В
0). Уравнение имеет вид: Ву
+ С
= 0 или у
= b,
где b
=
![]() .
Прямая проходит через точкуВ(0;
b),
она параллельна
оси Ох.
Число b
есть величина отрезка, который отсекает
прямая на оси Оу
(рис. 2).
.
Прямая проходит через точкуВ(0;
b),
она параллельна
оси Ох.
Число b
есть величина отрезка, который отсекает
прямая на оси Оу
(рис. 2).
Рис. 2
Если b = 0, то прямая совпадает с осью абсцисс Ох. Уравнение оси абсцисс Ох имеет вид: у = 0.
Уравнение прямой в отрезках на осях определяется уравнением:
![]() ,
,
г де
числаа
и b
являются величинами отрезков, отсекаемых
прямой на координатных осях (рис. 3).
де
числаа
и b
являются величинами отрезков, отсекаемых
прямой на координатных осях (рис. 3).
Рис. 3
Уравнение прямой,
проходящей через данную точку М(х0;
у0)
перпендикулярно
нормальному вектору
![]() = {A;
B},
определяется по формуле:
= {A;
B},
определяется по формуле:
А(х – х0) + В(у – у0) = 0.
Уравнение
прямой, проходящей через данную точку
М(х0;
у0)
параллельно
направляющему
вектору
![]() = {l;
m},
имеет вид:
= {l;
m},
имеет вид:
![]() .
.
Уравнение прямой, проходящей через две данные точки М1(х1; у1) и М2(х2; у2), определяется уравнением:
![]() .
.
Угловым коэффициентом прямой k называется тангенс угла наклона прямой к оси Ох, который отсчитывается от положительного направления оси к прямой против часовой стрелки, k = tgα.
Уравнение прямой с угловым коэффициентом k имеет вид:
у = kх+b,
где k=tgα,b – величина отрезка, отсекаемого прямой на осиОу (рис. 4).
Уравнение прямой, проходящей через данную точку М(х0; у0) в данном направлении(угловой коэффициентk известен), определяется по формуле:
у – у0=k(х– х0).
Уравнение пучка прямых, проходящих через данную точку М(х0; у0) (угловой коэффициентkнеизвестен), определяется по формуле:
у – у0=k(х– х0).

Рис. 4
Уравнение пучка прямых, проходящих через точку пересечения прямых
А1х+В1у+С1= 0 иА2х+В2у+С2= 0, определяется по формуле:
α(А1х+В1у+С1) + β(А2х+В2у+С2) = 0.
Угол , отсчитанный против часовой стрелки от прямойу = k1х+b1к прямой у = k2х+b2, определяется формулой (рис. 5):
![]() .
.

Рис. 5
Для прямых, заданных общими уравнениями А1х+В1у+С1= 0 иА2х+В2у+С2= 0, угол между двумя прямыми определяется по формуле:
![]() .
.
Условие
параллельности двух прямых имеет вид:k1=k2или![]() .
.
Условие
перпендикулярности двух прямых имеет
вид:![]() илиА1А2+В1В2= 0.
илиА1А2+В1В2= 0.
Нормальное уравнение прямойимеет вид:
x cosα + y sinα – p = 0,
где p – длина перпендикуляра, опущенного из начала координат на прямую,α– угол наклона перпендикуляра к положительному направлению осиОх (рис. 6).

Рис. 6
Чтобы привести
общее уравнение прямой Ах+Ву+С= 0 к нормальному виду, нужно все
его члены умножить нанормирующий
множитель μ=![]() ,взятый со знаком,
противоположным знаку свободного члена
С.
,взятый со знаком,
противоположным знаку свободного члена
С.
Расстояние от точки М(х0; у0) до прямой Ах + Ву + С = 0 определяется по формуле:
![]() .
.
Уравнения биссектрис углов между прямыми А1х+В1у+С1= 0 иА2х+В2у+С2= 0 имеют вид:
 .
.
Пример 4. Даны вершины треугольника АВС: А (–5; –7), В (7; 2), С (–6; 8). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол В; 4)уравнение медианы АЕ; 5) уравнение и длину высоты СD; 6) уравнение биссектрисы АК; 7) уравнение прямой, проходящей через точку Е параллельно стороне АВ; 8) координаты точки М, расположенной симметрично точке А относительно прямой СD.
Решение.
1. Расстояние d между двумя точками А(х1; у1) и В(х2; у2) определяется по формуле:
![]() .
.
Найдем длину стороны АВ как расстояние между двумя точками А(–7; –8) и В(8; –3):
![]() .
.
2. Уравнение прямой, проходящей через точки А(х1; у1) и В(х2; y2), имеет вид:
![]() .
.
Подставляя координаты точек А и В, получим уравнение стороны АВ:
![]() ;
;
Преобразуем последнее уравнение:
![]() ;
;
3(х + 5) = 4(у + 7); 3х – 4у – 13 = 0 (AВ).
Для нахождения углового коэффициента kAB прямой (АВ) разрешим полученное уравнение относительно у:
4y = 3x – 13;
![]() –уравнение прямой
(АВ)
с угловым
коэффициентом,
–уравнение прямой
(АВ)
с угловым
коэффициентом,
откуда
![]() .
.
Аналогично подставляя координаты точек В и С, получим уравнение прямой (ВС):
![]() ;
; ![]() ;
;
6х – 42 = –13у + 26; 6x + 13y – 68 = 0 (BC).
Разрешим уравнение
прямой (ВС)
относительно
у:
![]() .
.
Отсюда
![]() .
.
3. Тангенс угла между двумя прямыми, угловые коэффициенты которых равны k1 и k2, определяется по формуле:
![]() .
.
Внутренний угол
В
образован прямыми (АВ)
и (ВС),
причем это острый угол, на который надо
повернуть прямую ВС
в положительном направлении (против
часовой стрелки) до ее совпадения с
прямой (АВ).
Поэтому подставим в формулу k1
= ![]() ,
k2
=
,
k2
=
![]() :
:
 .
.
В
= arctg
![]() =arctg
1,575
57,59°.
=arctg
1,575
57,59°.
4. Чтобы найти уравнение медианы (АЕ), определим сначала координаты точки Е, которая является серединой стороны ВС. Для этого применим формулы деления отрезка на две равные части:
![]() .
.
Тогда
![]() .
.
Следовательно, точка Е имеет координаты: Е(0,5; 5).
Подставляя в уравнение прямой, проходящей через две точки, координаты точек А и Е, находим уравнение медианы (АЕ):
![]() ;
;
24х – 11у + 43 = 0(АЕ).
5. Так как высота CD перпендикулярна стороне АВ, то прямая (АВ) перпендикулярна прямой (CD). Для нахождения углового коэффициента высоты CD, воспользуемся условием перпендикулярности двух прямых:
![]() .
.
Тогда  .
.
Уравнение прямой, проходящей через данную точку М(х0; у0) в заданном направлении (угловой коэффициент k известен), имеет вид:
y – у0 = k (x – x0).
Подставляя в
последнее уравнение координаты точки
С(–6;
8) и ![]() ,
получим уравнение высоты CD:
,
получим уравнение высоты CD:
у– 8 =![]() (х
– (–6)), 3у– 24 = – 4х – 24, 4х+ 3у= 0 (CD).
(х
– (–6)), 3у– 24 = – 4х – 24, 4х+ 3у= 0 (CD).
Расстояние от точки М(х0;у0) до прямойАx + By + C =0 определяется по формуле:
![]() .
.
Длину высоты CD найдем как расстояние от точки С(–6; 8) до прямой (АВ): 3х – 4у – 13. Подставляя в формулу необходимые величины, найдем длину CD:
![]() (ед.).
(ед.).
6. Уравнения биссектрис углов между прямыми Аx + By + C =0 и А1x + B1y + C1 =0 определяются по формуле:
 .
.
Уравнение биссектрисы АКнайдем как одно из уравнений биссектрис углов между прямыми (АВ) и (АС).
Составим уравнение прямой (АС) как уравнение прямой, проходящей через две точкиА (–5; –7) и С (–6; 8):
![]() .
.
Преобразуем последнее уравнение:
![]() ;
;
15(х + 5) = – (у + 7); 15х + у + 82 = 0 (AС).
Подставляя коэффициенты из общих уравнений прямых (АВ) и (АС), получим уравнения биссектрис углов:
![]() .
.
Преобразуем последнее уравнение:
![]() ;
;
![]() (3х
– 4у
– 13) = ± 5 (15х +у +82);
(3х
– 4у
– 13) = ± 5 (15х +у +82);
3![]() х
– 4
х
– 4![]() у
– 13
у
– 13![]() = ± (75х
+5у
+ 410).
= ± (75х
+5у
+ 410).
Рассмотрим два случая:
3
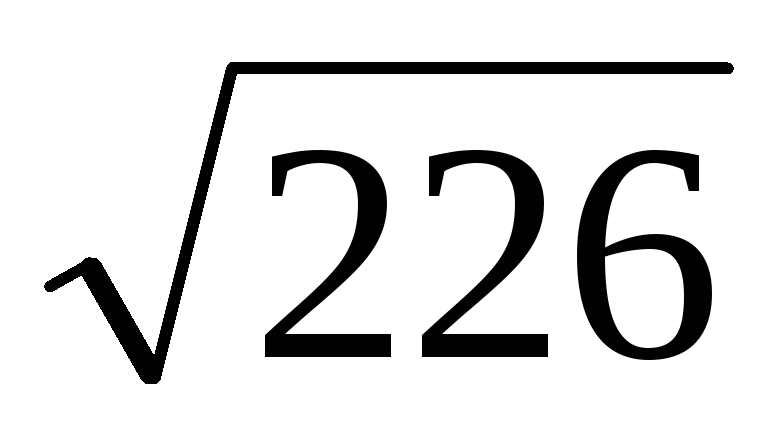 х
– 4
х
– 4 у
– 13
у
– 13 = 75х
+5у
+ 410.
= 75х
+5у
+ 410.
Тогда общее уравнение имеет вид:
(75
– 3![]() )х
+ (5 + 4
)х
+ (5 + 4![]() )у
+ 410 + 13
)у
+ 410 + 13![]() = 0.
= 0.
Определим
знак углового коэффициента прямой
![]() :
:
![]() .
.
Так
как
![]() ,
то угол наклона прямой является тупым
и, следовательно, данное уравнение не
является уравнением биссектрисы (АК).
,
то угол наклона прямой является тупым
и, следовательно, данное уравнение не
является уравнением биссектрисы (АК).
3
 х
– 4
х
– 4 у
– 13
у
– 13 = – (75х
+5у
+ 410).
= – (75х
+5у
+ 410).
Тогда общее уравнение имеет вид:
(75
+ 3![]() )х
+ (5 – 4
)х
+ (5 – 4![]() )у
+ 410 – 13
)у
+ 410 – 13![]() = 0.
= 0.
Так
как
![]() ,
то угол наклона прямой является острым
и, следовательно, данное уравнение
является уравнением биссектрисы (АК).
,
то угол наклона прямой является острым
и, следовательно, данное уравнение
является уравнением биссектрисы (АК).
(75
+ 3![]() )х
+ (5 – 4
)х
+ (5 – 4![]() )у
+ 410 – 13
)у
+ 410 – 13![]() = 0 – уравнение биссектрисы (АК).
= 0 – уравнение биссектрисы (АК).
7. Так как искомая прямая l параллельна сторонеАВ, то из условия параллельности двух прямых ее угловой коэффициент равен угловому коэффициенту прямой (АВ):
kl
= kAB
=![]() .
.
Подставляя в
уравнение прямой, проходящей через
данную точку в данном направлении
координаты точки Е и угловой
коэффициентkl
= ![]() ,получим уравнение прямойl:
,получим уравнение прямойl:
![]() ;
3х–4у+ 18,5 = 0.
;
3х–4у+ 18,5 = 0.
8. Так как прямая (АВ) перпендикулярна прямой (CD), то искомая точка М, расположенная симметрично точке А относительно прямой (CD), лежит на прямой (АВ). Кроме того, точка D является серединой отрезка AM. Применим формулы деления отрезка на две равные части:

Точка Dлежит на пересечении высотыCDи основанияАВ. Для нахождения ее координат решим систему уравнений, составленную из уравнений прямых (АВ) и (CD):


Точка D имеет координаты (1,56; –2,08).
Найдем координаты искомой точки M:
![]()
Точка M(8,12; 2,84) лежит на продолжении стороны АВ.
Треугольник АВС, высота CD, медиана АЕ, биссектриса АК, прямая l и точка М построены в системе координат Оху (рис.7).

Рис.7
