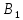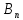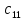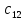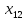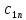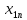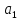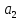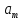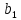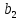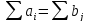1.4 Сызықтық программалау есебін шешудің симплекс әдісі.

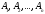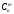Сызықтық программалау есебінің оптималдық шешімі тірек шешімдерінің ішінен іздестіріледі, әрбір тірек шешімі берілген n векторлар жүйесіндегі m сызықтық тәуелсіз вектролармен анықталғандықтан, олардың саны терулерінің санынан аспайды.

m және n сандары жеткілікті үлкен болғанда оптималдық шешімді барлық тірек шешімдерін құру арқылы іздестру өте қиын.

Симплекс әдісі белгілі тірек шешімінен келесі жақсартылған трек шешіміне көшіріп отырады, санаулы қадымнан соң оптималдық шешімге келтіріледі; есептің шешімі жоқ немесе сызықтық функциясы шектеусіз болса, оны да көрсетеді.

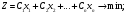
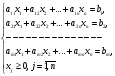
есебін қарастырайық және мұндағы 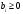, 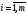болсын.

Шектеулер жүйесінің алғашқы m векторлары бірлік векторлар балсын делік. Онда есеп мына түрде қойылады

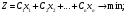(1.4.1)

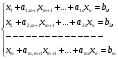(1.4.2)

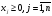(1.4.3)

Теңдеулер жүйесін (1.4.2) векторлық түрде жазайық

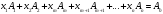(1.4.4)

мұндағы

, , … , , , … , ,

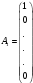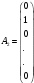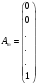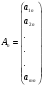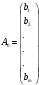
m-өлшемді кеңістіктің сызықтық тәуелсіз 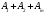векторлары осы кеңістіктің базисін жасайтындықтан, (1.4.4) жіктелуіндегі 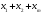айнымалыларын базистік деп, 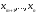еркін айнымалыларын нөлге теңестірп, 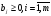болғандықтан алғашқы

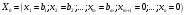(1.4.5)

шешімін аламыз. Осы шешімге сәйкес

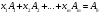(1.4.6)

жіктелуіндег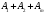і векторлары сызықтық тәуелсіз, демек құрылған алғашқы шешім есептің тірек шешімін береді.

Бастапқы тірек шешімнен (1.4.5) келесі тірек шешімді қалай құратындығын қарастырайық. m-өлшемді кеңістіктің (1.4.4) өрнектегі әрбір векторы базистік 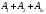векторлары арқылы бір ғана түрде былай жіктеледі

,

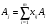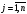
Базиске енбеген, мысалы 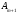векторының,

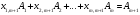(1.4.7)

әйтеуір бір коэфифициенті 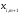оң таңбалы болсын делік. Әзірге белгісіз 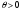шамасына (1.4.7) теңдікті көбейтіп, (1.4.6) теңдіктен шегерсек,

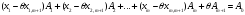(1.4.8) теңдігін аламыз. Сонымен

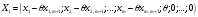
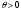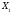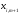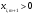Векторының компоненттері теріс таңбалы болмаса, шешімді береді. болғандықтан, - векторының теріс таңбалы -лер енетін компоненттері теріс таңбалы бола алмайды. Сондықтан кезкелген үшін

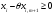(1.4.9) болатындай мәнін табу қажет. (1.4.9) теңсіздіктен

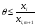
демек

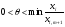, (1.4.10)

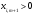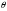шартын орындайтын кезкелген үшін 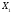векторы есептің шешімін береді.

Тірек шешмінің m+1 оң таңбалы компоненті болмайтындықтан, 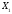шешімінің 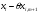, , 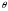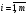компоненттерінің кемінде біреуін нөлге айналдыру қажет. (1.4.10) теңсіздіктегі мәнін алсақ 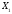шешімінің min қабылдайтын компоненті нөлге айналады. Бұл компонент бірінші орындағы, яғни 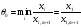болсын делік. 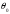мәнін (1.4.8)-ге қойып

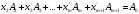
жіктелуін аламыз, бұл жаңа тірек шешімі

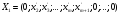
сәйкес. Мұндағы

,

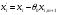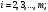
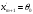
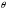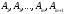арқылы базистен векторды шығарып, орнына жаңа вектор енгізуді бізде Жордан – Гаусс әдісімен бір базистен екінші базиске көшу болғандықтан, векторлар жүйесі сызықты тәуелсіз және жаңа базисті береді. Жаңа тірек шешімді құру базиске енгізілетін векторды таңдаудан және базистен шығарылатын векторды анықтаудан тұрады. Симплекс әдісінің негізгі элементтерінің бірі базиске енгізілетін векторды анықтау белгісі. Егер 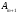базиске енгізілетін вектор ретінде анықталып, оның жіктелуіндегі (1.4.7) барлық

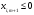
болса, онда (1.4.8) жіктелуінен бір векторды шығаратындай 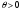таңдау мүмкін емес. Бұл жағдайда 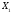шешімі m+1 оң таңбалы компонентті, ал

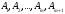
вектролар жүйесі сызықты тәуелді болып, шешімдер көпжағының сызықтық функция min мәнін қабылдай алмайтын, бұрыштық емес, ішкі нүктесін анықтайды. Сондай-ақ, бұл, сызықтық функция гипержазықтығы 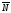векторына қарама-қарсы бағыттағы қандай қашықтықта болса да шешімдер көпжағына тірек жазықтық бола алмайтынын, яғни сызықтық функция шешімдер көпжағында шектеусіз екендігін көрсетеді.

Сонымен сызықтық программалау есебінің бос мүшелері теріс таңбалы емес шектеулер жүйесі құрамында бірлік базис болса, онда қосымша есептеулерсіз-ақ алғашқы тірек шешімін, сондай-ақ векторлардың базиске жіктелу коэффициенттерін алуға болады.

Мысал.

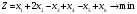
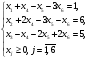
Тірек шешімін құрып, жаңа тірек шешіміне көшу керек.

Шешуі. Теңдеулер жүйесін векторлық түрде жазсақ

ЕСЕП ЖАЗ

Енді симплекс әдісінің оптималдық шешімін табу және оcы әдістің оптималдық шарттарын құрайық.

,

,

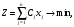
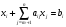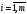
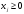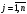
есебінің шешімдері бар және әрбір тірек шешімі ұүнарлы делік. Онда

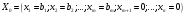
тірек шешіміне

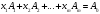(1.4.11)

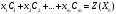(1.4.12)

,

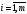
ал кезкелген 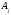векторына берілген 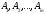базисінде

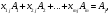(1.4.13)

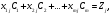(1.4.14)

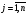
теңдіктері тиесілі.

Сызықтық функцияның 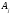векторына сәйкес коэффициентін 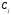деп белгілейміз. Онда келесі теорема орындалады.

Теорема 1. Егер әйтеуір бір векторына 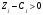шарты (белгісі) орындалса, онда 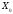шешімі оптималды емес және 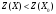теңсіздігі орындалатын Х шешімін құруға болады.

Дәлелдеуі. (1.4.13) және (1.4.14) теңдіктерін 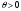-ға көбейтіп, (1.4.11) және (1.4.12) теңдіктерінен шегереміз

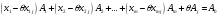, (1.4.15)

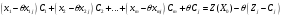(1.4.16)

Теңдіктің екі жағына да 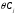қосылған. Бұл теңдіктердегі 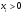, , 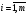сондықтан - лер түгелімен дерлік оң таңбалы болатындай 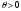- ны табуға болады. Демек, есептің жаңа шешімін

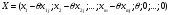
және оған (1.4.16)- шы өрнек бойынша тиісті сызықтық функцияның

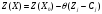
мәнін аламыз. Теорема шартында 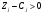және 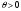, онда

.

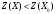Салдар. Егер әйтеуір бір шешім 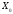-дің базисінде барлық 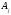, 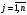векторларының жіктеулеріне

(1.4.17)

шарты (белгісі) орындалса, онда шешім 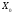- оптималды.

Сызықтық функцияның min мәнін табу есептің оптималдық шарты (белгісі) (1.4.17) теңсіздіктерімен анықталады, ал 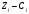мәндері шешім бағалары деп аталады.

Сонымен, сызықтық функция min –мын табу есебінің шешімі оптималды болуы үшін оның бағаларының оң таңбалы болмауы қажетті және жеткілікті.

Сызықтық программалаудың сызықтық функция max –мын мәнін табу есебі үшін келесі теорема орынды.

Теорема 2. Егер әйтеуір бір 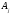векторына 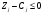шарты (белгісі) орындалса, онда 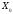шешімі оптималды емес және 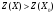болатын Х шешімін құруға болады.

Дәлелдеуі. Теорема 1 –дегідей.

Салдар. Егер әйтеуір бір шешім 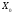-дің базисінде барлық 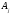, 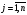векторларының жіктеулеріне

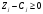(1.4.18)

Шарты (белгісі) орындалса, онда шешім 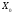оптималды.

(1.4.18) теңсіздіктері сызықтық функцияның max мәнін табу есебінің оптималдық шарты (белгісі).

Сонымен, сызықтық функция max –мын табу есебінің шешімі оптималды болуы үшін оның бағаларының теріс таңбалы болмауы қажетті және жеткілікті.

д

Сызықтық программалаудың транспорт есебі транспорт пен өнеркәсіп және өндірістің түрлі мәселелерінің теориялық зерттеулерінде және практикада жиі қолданылады. Әсіресе өнеркәсіп пен ауылшаруашылық өнімдерін жеткізуді рационализациялауда, сондай – ақ жүк айналымдарын оптималды жоспарлауда және транспорттың басқа да әртүрлі жұмыстарында ерекше маңызы бар. Барлығы m ұсынушыда, 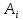-де , , 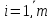жинақталған біртекті заттарды, барлығы n тұтынушыға, 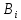-де 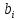, 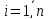жеткізу керек. Бірлік жүкті і - ұсынушыдан j-тұтынушыға тасымалдау бағасы 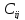белгілі.

Тұтынушылар сұранысын толық қанағаттандыратын және бағасы минималды болатын, барлық жүкті тасымалдау жоспарын құру қажет.і - ұсынушыдан j-тұтынушыға тасымалдауға жоспарланған жүкті 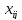деп белгілеп, есептің шартын жоспарлау матрицасы аталатын кестемен жазуға болады.

Ұсынушылар	Тұтынушылар					Қорлар
A1	x11		…
А2	c21 x21	c22 х22	…	c2n x2n
...	…	…	…	…	…
Ат	cm1 xm1	cm2 xm2	…	cmn xmn
Сұраныстар			…

Есептің математикалық моделін құрайық .

i-ұсынушыдан j-тұтынушыға тасымалданатын жүк x_ij, оның тасымал бағасы C_ijx_ij. Барлық жүкті тасымалдау бағасы

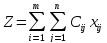
Шектеулер жүйесін есептің келесі шарттарынан аламыз:

1. Барлық жүк тасымалдануы керек, яғни

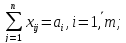
(бұл теңдеулер кестенің жолдарынан алынады).

2. Сұраныстар түгелімен қанағаттандырылуы керек, яғни

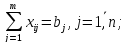
(бұл теңдеулер кестенің бағандарынан алынады).

Сонымен, транспорт есебінің математикалық моделі келесі түрде беріледі.

Сызықтық функцияның

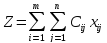
ең кіші мәнін келесі шектеулерде

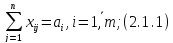
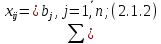
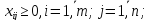
табу керек.

Қарастырып отырған моделде қорлар қосындысы сұраныстар қосындысына тең деп есептелінеді.

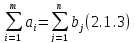
Бұндай модель тұйықталған (жабық) деп аталады.

Теорема.

Қорларының қосындысы сұраныстарының қосындысына тең болатын кез-келген транспорт есебінің шешімі бар.

Теореманы дәлелдеу үшін, берілген шарттарда кемінде бір шешімі бар екендігін және сызықтық функция шешімдер жиынында шектеулі екендігін көрсету қажет.

Дәлелдеуі.

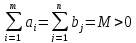
делік , онда:

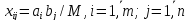
шамалары (2.1.1), (2.1.2) шектеулер жүйелерін қанағаттандыратындықтан, есептің шешімі болады. Шындығында да, 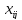мәндерін (2.1.1) және (2.1.2)-ке қойсақ, табамыз

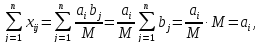
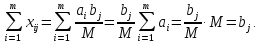
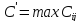мәнін алып, сызықтық функцияны бағаласақ, (2.1.2) теңдік арқылы мынаны аламыз

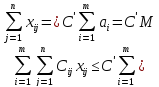
Дәл сол сияқты 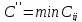мәнін қолдансақ

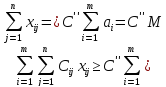
Соңғы екі теңсіздікті біріктіріп қарастырсақ теңсіздігін аламыз, яғни сызықтық функция транспорт есебі шешімдерінің жиынында шектеулі.