
- •§ 4. Линейные дифференциальные уравнения высших порядков
- •§ 5. Линейные однородные уравнения
- •§ 6. Линейное однородное уравнение с постоянными коэффициентами
- •§ 7. Линейные неоднородные уравнения
- •§ 10. Интегрирование дифференциальных уравнений с помощью рядов
- •§ 12. Краевые задачи в линейных дифференциальных уравнениях
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Литература
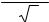
9.8 Найти интегральную кривую уравнения yy′′ + y′2 = 1, проходящую через точку (0,1) и касающуюся в этой точке прямой x + y = 1 (почему получается
одна интегральная кривая ?). |
|
|
10.8 Частица массы m движется по оси Ox , отталкиваясь от точки x = |
0 |
с |
силой 3mr0 и притягиваясь к точке x = 1 с силой 4mr1 , где r0 и |
r1 |
- |
расстояние до этих точек. Определить движения частицы с начальными
условиями x(0) = |
|
|
|
|
& |
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2, x(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1.9 |
x3 y′′′ + |
|
x2 y′′ |
= |
|
|
1 |
|
|
|
|
|
|
|
|
|
Вариант 9 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2.9 |
yy |
′′ |
− |
|
|
y |
′2 |
= |
|
|
y |
2 |
; |
|
|
y(0) = |
1, y |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3.9 |
x |
2 |
yy |
′′ |
|
= |
|
|
(y − |
|
|
|
|
|
|
|
′ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
xy ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4.9 |
64y viii + |
|
48y vi |
|
+ |
|
|
12 y′v |
+ y′′ = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
5.9 |
y(0) = |
|
0, y′(0) = 0, y′′(0) = |
0, y′′′(0) = |
1, y′v (0) = |
1, yv (0) = 0, yvi (0) = |
1, yvii (0) = |
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
y′′′ − |
|
|
4 y′ = |
|
3 + |
|
|
e2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
6.9 |
y''+ |
|
y = |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
sin x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7.9 |
x |
2 |
y |
′′ |
|
+ |
|
3xy |
′ |
+ |
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 (до x |
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
8.9 |
y |
′′ |
|
= |
|
|
|
y + |
|
|
x |
2 |
+ |
|
|
y |
′2 |
; |
|
|
|
|
|
′ |
5 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(0) = 1, y (0) = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
9.9 |
Найти интегральную кривую уравнения |
′ |
′′ |
= |
y |
′3 |
+ |
y |
′′2 |
, касающуюся в |
|||||||||||||||||||||||||||||||||||
yy y |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
начале координат прямой x + y = |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
10.9 |
|
|
Электрическая цепь состоит из последовательно включенных |
||||||||||||||||||||||||||||||||||||||||||
источников постоянного тока, дающего напряжение U , сопротивления R , |
|||||||||||||||||||||||||||||||||||||||||||||
самоиндукции |
|
|
|
L |
|
|
и выключателя, который включается при t = 0 . Найти |
||||||||||||||||||||||||||||||||||||||
зависимость силы тока от времени (при t > 0 ). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 10 |
|
|
|
|
|
|
|
|
|
||||
1.10 |
xy′′′ − |
|
|
y′′ + |
|
|
|
= |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2.10 |
yy |
′′ |
|
= |
|
|
y |
′2 |
; |
|
|
|
|
y(0) = |
|
|
′ |
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1, y (0) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3.10 |
y(xy |
′′ |
+ |
|
|
|
′ |
|
|
|
= |
|
xy |
′2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
y ) |
|
|
|
|
(1 − x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
4.10 |
y |
′′′ |
= |
|
− |
|
|
′ |
|
|
|
|
y(0) = |
|
|
′ |
= |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
y ; |
|
|
|
2, y (0) |
0, y (0) = − 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
5.10 |
y′v |
|
− |
|
5 y′′′ + |
|
|
6 y′′ |
|
= |
2x + |
sin 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6.10 |
y′′ − |
|
|
|
y = |
|
4x2 |
|
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7.10 |
x |
2 |
y |
′′ |
− |
|
3xy |
′ |
+ |
|
|
4 y = |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
43

8.10 |
(1 + x |
2 |
)y |
′′ |
+ xy |
′ |
− y = 0; |
y(0) |
′ |
3 |
) |
|
|
|
= 1, y (0) = 1 (до x |
|
|||||||
9.10 |
Последовательно включены источники тока, напряжение каждого |
||||||||||
меняется по закону E = |
v sin ω |
t , сопротивление R и самоиндукция L . Найти |
|||||||||
силу тока в цепи (установившийся режим). |
|
|
|||||||||
10.10 Найти плоские кривые, радиус кривизны которых пропорционален кубу длины отрезка нормали.
1.11 |
|
′ |
|
′′′ |
= |
|
|
2 y |
′′2 |
|
|
|
|
|
|
Вариант 11 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2.11 |
2 yy′′ = |
|
y′2 ; |
y(− |
1) = 4, y′(− 1) = |
1 |
|
|
|
|||||||||||||
3.11 |
x2 yy′′ + |
|
|
y′2 |
|
= |
0 |
|
y(0) = |
|
0, y (0) |
= |
0, y (0) |
= |
1, y (0) |
= 2 |
||||||
4.11 |
y |
′v |
|
+ |
2y' '+ |
y = |
0; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
′′ |
|
′′′ |
|
|
5.11 |
y v |
+ |
y′′′ |
= |
|
x2 |
+ 5 |
|
|
|
|
|
|
|
|
|||||||
6.11 |
y |
′′′ |
+ |
y |
′ |
= |
|
|
sin x |
|
|
|
|
|
|
|
|
|
||||
|
cos2 x |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
7.11 |
(x2 |
|
− |
1) y′′ + |
|
xy′ − |
2 y = |
0 |
|
|
|
|
|
|||||||||
8.11 |
y |
′′ |
− xy |
′ |
− y = |
0; |
|
y(0) = |
′ |
|
= 0 |
|
|
|
||||||||
|
|
|
1, y (0) |
|
|
|
||||||||||||||||
9.11 Найти уравнение кривой, касающейся оси абсцисс в начале кординат,
|
|
π |
|
|
π |
|
|||
если ее кривизна в любой точке равна cos x |
− |
|
|
< |
x < |
|
|
. |
|
2 |
2 |
||||||||
|
|
|
|
|
|||||
10.11 Найти закон движения тела, падающего в воздухе без начальной скорости, считая сопротивление воздуха пропорциональным квадрату скорости.
1.12 |
y′′′ |
= |
2( y′′ − |
1)ctgx |
|
|
Вариант 12 |
||||||||||||
|
|
|
|
|
|||||||||||||||
2.12 |
y |
′2 |
|
+ |
|
yy |
′′ |
= |
|
|
′ |
|
′ |
= |
2 |
|
|
||
|
|
|
|
|
yy ; |
y(0) = 1, y (0) |
|
|
|||||||||||
3.12 |
xyy |
′′ |
= |
|
|
′ |
|
+ |
|
′ |
|
|
|
|
|
|
|||
|
y |
( y |
y ) |
|
|
|
|
|
|
||||||||||
4.12 |
y |
′′′ |
− |
4 y |
′′ |
+ 5y |
′ |
= |
0; y(0) = |
|
′ |
|
′′ |
= 2 |
|||||
|
|
|
|
0, y (0) = |
1, y (0) |
||||||||||||||
5.12 |
y′v − |
|
y = |
|
x2 + |
|
ex |
|
|
|
|
|
|
||||||
6.12 |
y′′ − |
|
y′ = |
|
|
e2 x |
1 − |
e2 x |
|
|
|
|
|
||||||
7.12 |
x2 y′′ − 6 y = 12 ln x |
|
|
|
π |
(до x |
|
) |
||||
8.12 |
y |
′′ |
= |
′ |
= |
′ |
= |
4 |
||||
|
3 |
|
||||||||||
|
xy cos y ; y(0) |
1, y (0) |
|
|||||||||
9.12 Найти уравнения кривых, у которых радиус кривизны в любой точке равен длине отрезка нормали, заключенного между этой точкой и осью абсцисс, если кривая вогнута вверх.
44

10.12 Мяч массой 400г падает с высоты 16,7м без начальной скорости. Сопротивление воздуха пропорционально скорости мяча и равно 0,0048Н при скорости 1 м/с. Вычислить время падения и скорость мяча в конце падения. Принять g=10 м/с2.
Вариант 13
1.13 |
x2 y′′′ = |
|
y′′2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.13 |
x |
2 |
y |
′′ |
− |
3xy |
′ |
= |
6 y 2 |
|
− |
4 y ; |
y(1) = 1, |
|
′ |
|
4 |
|||||||
|
|
x2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
y (1) = |
||||||||||||||||||
3.13 |
x |
|
y |
′′ |
= |
( y − |
|
xy )( y |
|
− |
xy |
′ |
− |
x) |
|
|
|
|
|
|||||
|
|
3 |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
||
4.13 |
y |
′′′ |
− |
|
3y |
′ |
+ |
2 y = |
0; |
|
|
y(0) = |
|
′ |
= |
′′ |
|
|||||||
|
|
|
|
|
|
0, y (0) |
1, y (0) = − 1 |
|||||||||||||||||
5.13 |
y′′′ − |
|
3y′ + |
2 y = |
e− |
|
x x |
|
|
|
|
|
|
|
|
|||||||||
6.13 |
y′′ + |
|
y = |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
cos 2x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7.13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 y′′′ − |
3xy′′ + 3y′ |
= |
0 |
|
|
|
|
(до x |
|
) |
||||||||||||||
8.13 |
y |
′′ |
|
= |
|
xy |
2 |
− |
|
′ |
|
|
|
|
|
|
|
′ |
= 1 |
4 |
||||
|
|
|
|
y ; |
|
y(0) = 2, y (0) |
|
|||||||||||||||||
9.13 Найти уравнение кривых, у которых радиус кривизны в любой точке равен длине отрезка нормали заключенного между этой точкой и осью абсцисс, если кривая вогнута вниз.
10.13 Тело массы m движется прямолинейно под действием постоянной силы p . Найти скорость движения и пройденный им путь как функцию
времени, если в начальный момент они оба равны нулю, а сопротивление среды пропорционально квадрату скорости.
1.14 |
y′′′ |
= |
y′′2 |
|
|
|
|
|
|
|
|
|
|
|
Вариант 14 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2.14 |
2 yy |
′′ |
= |
y |
′2 |
; |
y(− |
1) = |
′ |
1) = 1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
4, y (− |
|
|
|
|
|
|
|
||||||||||||||||
3.14 |
x2 (2 yy′′ − |
|
y′2 ) = |
|
1 − |
2xyy′ |
|
|
|
|
|
|
|
|
|
|||||||||||
4.14 |
y |
′v |
|
+ |
8y |
′′ |
+ |
|
16 y = |
0; |
y(0) = |
′ |
= |
′′ |
|
|
= 1, y |
′′′ |
= 1 |
|||||||
|
|
|
|
|
0, y |
(0) |
1, y (0) |
(0) |
||||||||||||||||||
5.14 |
y′v |
|
− |
y = |
|
5ex sin x |
|
|
|
|
|
|
|
|
|
|
||||||||||
6.14 |
y′′ − 2 y′ = |
|
|
4e− 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 + |
e− |
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7.14 |
x2 y′′′ − |
2 y′ = |
0 |
|
|
|
|
|
|
|
|
(до x |
|
) |
|
|
|
|||||||||
8.14 |
y |
′′ |
= |
|
xy |
′ |
− |
|
y + |
e |
x |
; |
|
|
|
′ |
= 1 |
|
4 |
|
|
|
||||
|
|
|
|
|
|
y(0) = 1, y (0) |
|
|
|
|
|
|||||||||||||||
9.14 Найти кривые постоянного радиуса кривизны.
10.14 Найти закон прямолинейного движения материальной точки массы m под действием отталкивающей силы, обратно пропорциональной кубу расстояния от точки до неподвижного центра. В начальный момент точка находится в покое и отстоит от центра на расстояние x0 .
45
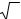
|
|
|
|
|
|
y − |
xy′ |
|
|
|
|
|
|
|
Вариант 15 |
|
|
||||||||||
1.15 |
y′′ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
yy |
′′ |
= |
|
y |
′ |
2 |
− |
y |
′3 |
|
|
|
′ |
|
= |
2 |
|
|
|
|
|
||||||
|
|
|
|
|
; y(0) = 1, y (0) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
3.15 |
x |
2 |
yy |
|
= |
( y − |
xy ) |
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4.15 |
y |
′v |
+ |
|
2 y |
′′ |
+ |
y = |
|
|
|
|
′ |
|
|
′′ |
= 1, y |
′′′ |
= 2 |
||||||||
|
|
|
|
0; y(0) = 0, y (0) |
= 0, y (0) |
(0) |
|||||||||||||||||||||
5.15 |
y′v |
+ |
|
2 y′′ + |
y = |
x2 sin x |
|
|
|
|
|
|
|
|
|||||||||||||
6.15 |
y |
′′ |
+ |
9 y = |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
cos 3x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
7.15 |
(2x + |
1) y′′ + 4xy′ − |
4 y = 0 |
|
|
(до x |
|
) |
|
|
|
||||||||||||||||
8.15 |
y |
′′ |
= |
|
xy |
′ |
+ |
|
e |
y |
; |
y(0) = |
′ |
= |
1 |
6 |
|
|
|
||||||||
|
|
|
|
|
|
0, y (0) |
|
|
|
|
|||||||||||||||||
9.15 Найти кривые, у которых радиус кривизны равен нормали.
10.15 Материальная точка массы m движется прямолинейно к неподвижному центру, притягивающему ее силой, обратно пропорциональной кубу расстояния от точки до неподвижного центра. В начальный момент точка находится в покое и отстоит от центра на расстояние x0 . Определить время, по истечении которого точка достигает
центра.
|
|
y′′2 |
− y′y′′′ |
|
|
|
|
|
|
|
|
|
|
Вариант 16 |
|
|
|
|
|
|||||||||||
1.16 |
|
= |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y′2 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2.16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y |
3 |
y |
′′ |
= 1; |
|
|
y(− |
2) = |
′ |
|
− 1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1, y (− 2) = |
|
|
|
|
|
|
|
|
|||||||||||||||||
3.16 |
4x2 y3 y′′ = |
x2 |
|
− |
y4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4.16 |
|
y |
v |
+ |
|
y |
′′′ |
= |
|
0; |
|
|
|
|
|
|
|
′ |
= |
′′ |
= |
′′′ |
= |
1, y |
′v |
(0) |
= 1 |
|||
|
|
|
|
|
|
|
|
y(0) = 0, y (0) |
1, y (0) |
2, y (0) |
|
|||||||||||||||||||
5.16 |
|
y v |
+ |
|
y′′′ |
= |
|
x2 |
+ |
|
5 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
6.16 |
|
y |
′′ |
− |
6 y |
′ |
+ |
|
8 y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 + e− 2 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
7.16 |
|
x2 y′′ − |
|
2 y = |
|
sin ln x |
|
|
1 (до x |
|
) |
|
|
|
|
|
||||||||||||||
8.16 |
|
y |
′′ |
= |
|
yx |
2 |
+ |
|
y |
′3 |
; |
|
|
y(0) = |
′ |
= |
6 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
y (0) |
|
|
|
|
|
|
||||||||||||||
9.16 Найти кривую, у которой радиус кривизны пропорционален кубу нормали.
10.16 Балка длины l , лежащая концами на двух опорах, находится под действием равномерно распределенной нагрузки интенсивности q . Найти
уравнение прогнутой оси балки и ее максимальный прогиб, выбрав начало координат в середине нагруженной балки.
Вариант 17
1.17 |
x3 y′′′ + |
x2 y′′ = |
x |
|
|
|
||
2.17 |
′′ |
3 |
+ |
9 = 0; |
y(1) = |
1, |
′ |
= 3 |
y y |
|
y (1) |
||||||
46
