6.4. Сила трения качения
Этот вид трения проявляется при качении и связан не с деформацией зазубрин, а с деформацией дороги (прогиб) и самого колеса (небольшое сплющивание), рис. 6.5.
При качении по мягкому покрытию колесо вдавливается в опору, образуя ямку, через край которой ему все время приходится перекатываться, рис. 6.5, а. Французский физик Ш. Кулон на основе опытов нашел, что сила трения качения (FKa4) пропорциональна силе нормального давления N и обратно пропорциональна радиусу г колеса:
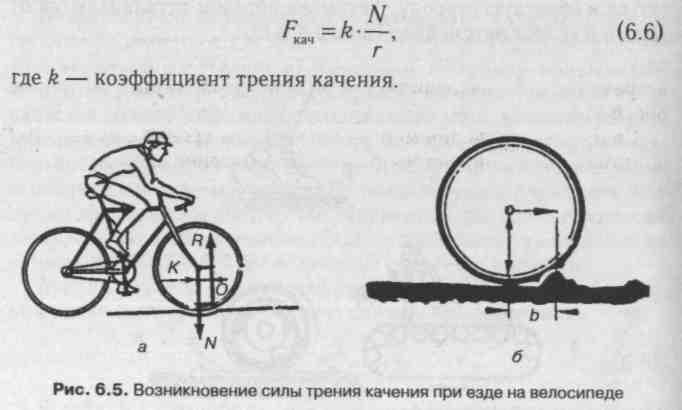
Из формулы видно, что коэффициент трения качения зависит от радиуса колеса и выражается в единицах длины (м или см). Значения коэффициента трения качения для некоторых веществ приведены в табл. 6.2.
При движении по твердому покрытию сила трения качения связана с деформацией самого колеса. С этой силой особенно приходится считаться в вело- и мотоспорте. Ее величина определяется по формуле:
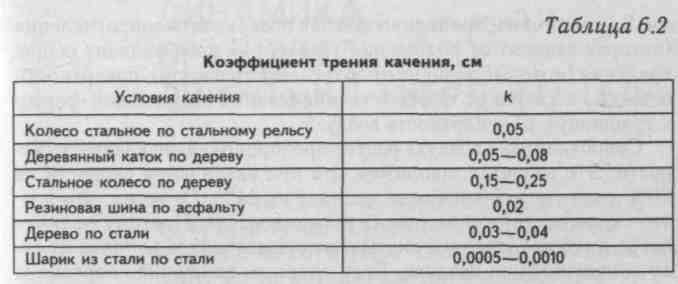
где N — сила нормального давления; Ь — расстояние между теоретической точкой опоры шины и фактической первой точкой встречи шины с поверхностью, по которой проходит перемещение, рис. 6.5, б.
Сила трения качения много меньше силы трения скольжения, поэтому колесо широко используется в различных видах транспорта.
6.5. Сила сопротивления при движении в жидкости или газе
Силы трения, рассмотренные выше, не зависели от скорости движения тела. Иначе обстоит дело при движении тела в жидкой или газообразной среде. Сила, действующая на тело в этом случае, называется силой сопротивления. Силы сопротивления очень зависят от формы тела и возрастают при увеличении скорости его движения относительно среды. Если тело не движется относительно среды,-то сила сопротивления равна нулю, т. е. аналога силе трения покоя в данном случае нет. Зависит сила сопротивления и от качества поверхности тела. Именно этим объясняется, что пловцы все чаще выступают в специальных костюмах, снижающих силу сопротивления.
Скорость спортсмена и сила сопротивления встречного потока воздуха связаны между собой следующим соотношением:
Глава 7
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
7.1. Плечо силы. Момент силы. Момент инерции тела. Кинетическая энергия вращающегося тела. Основное уравнение динамики вращательного движения
При вращении твердого тела относительно оси, скорости точек, лежащих на разных расстояниях от оси вращения, различны, в то время как угловые скорости всех его точек одинаковы. Поэтому для описания вращения твердого тела используют, в основном, угловую скорость и угловое ускорение его вращения. В подразделе (4.5) были введены понятия момента силы (4.12) и момента инерции (4.14) для материальной точки, с помощью которых был записан закон вращения (4.15). Распространим эти понятия на твердое тело, вращающееся вокруг оси (О) под действием некоторой силы. Если сила (F ) не перпендикулярна оси вращения, то ее раскладывают на две составляющие, одна из которых параллельна оси вращения, а вторая лежит в плоскости, перпендикулярной оси (рис. 7.1).
Составляющая силы, направленная параллельно оси (Fo), не может вызвать вращения (она стремится двигать тело вдоль оси) и в дальнейшем рассматриваться не будет. Поэтому при описании вращательного движения будем принимать во внимание только те
Момент и плечо силы определяются точно так же, как и для вращения материальной точки (рис. 7.2).
Плечом силы (/г), лежащей в плоскости, перпендикулярной оси вращения, называется кратчайшее расстояние от оси вращения до линии действия силы.
Моментом силы (М) относительно оси вращения называется произведение величины силы на ее плечо:
Момент силы берется со знаком «+», если сила стремится повернуть тело по часовой стрелке и со знаком «—» в противном случае (на рис. 7.2 момент силы F равен М = —F-h).
Моментом инерции твердого тела относительно оси называется сумма моментов инерции всех его точек.
Для тел, обладающих симметрией, момент инерции находится методом интегрирования. Для примера найдем момент инерции стержня массой т и длиной /, расположенного перпендикулярно оси, проходящей через его конец (рис. 7.3).
