
- •Міністерство освіти і науки україни
- •Частина I Елементи функціонального аналізу Розділ 1. Метричні простори § 1. Поняття метричного простору
- •§ 2. Нормований метричний простір
- •§ 3. Скалярний добуток
- •§ 4. Приклади метричних просторів
- •Розділ 2. Збіжність в метричних просторах § 1. Границя послідовності
- •Нехай маємо послідовність
- •§ 2. Збіжність в просторах Rn, l2, c[a;b]
- •Розділ 3. Відкриті і замкнені множини § 1. Деякі поняття теорії метричних просторів
- •§ 2. Замикання і його властивості
- •§ 3. Замкнені множини і їх властивості
- •§ 4. Відкриті множини і їх влативості
- •Розділ 4. Неперервні відображення § 1. Поняття функції
- •§ 2. Границя і неперервність функції
- •§ 3. Зв’язні множини. Збереження зв’язності при неперервних відображеннях
- •Розділ 5. Компактні множини § 1. Компакти і їх властивості
- •§ 3. Критерій компактності
- •§ 4. Властивості функцій неперервних на компакті
- •Розділ 6. Повні метричні простори § 1. Приклади повних метричних просторів
- •§ 2. Властивості повних метричних просторів
- •§ 3. Теорема Банаха
- •Частина II Диференціальне числення функцій багатьох змінних Розділ 1. Поняття дійсної функції багатьох змінних
- •Розділ 2. Диференційовність функцій багатьох змінних § 1. Поняття диференційовної функції. Часткові похідні. Необхідні умови диференційовності
- •§ 2. Достатні умови диференційовності функції багатьох змінних
- •§ 3. Диференційовність складної функції.
- •§ 4. Інваріантність форми диференціала функції багатьох змінних.
- •§ 5. Похідна за напрямком. Градієнт.
- •Розділ 3. Частинні похідні і диференціали вищих порядків § 1. Частинні похідні вищих порядків
- •§ 2. Достатні умови незалежності змішаних частинних похідних від порядку диференціювання.
- •§ 3. Диференціали вищих порядків
- •§ 4. Формула Тейлора для функцій багатьох змінних
- •Розділ 4. Неявні функції § 1. Існування неявної функції однієї змінної
- •§ 2. Існування неявної функції багатьох змінних
- •§ 3. Існування неявної функції, яка задається системою рівнянь
- •Розділ 5. Екстремуми функцій § 1. Поняття екстремума функцій багатьох змінних
- •§ 2. Деякі відомості з теорії квадратичних форм
- •§ 3. Достатні умови існування екстремуму
- •§ 4. Умовний екстремум
- •Частина III. Розробка електронного посібника “Елементи функціонального аналізу та диференціальне числення функцій багатьох змінних”
- •Програмне середовище підручника
- •Як працювати з підручником?
- •Висновки
- •Часть II.– м.: ”Наука”, 1993. – 448с.
§ 3. Скалярний добуток
Означення
3.1. Нехай
маємо лінійну систему Х.
Говорять, що на лінійній системі Х
введено
скалярний добуток,
якщо будь-якій парі елементів
![]() і
і![]() із цієї системи ставиться у відповідність
дійсне число
із цієї системи ставиться у відповідність
дійсне число![]() ,
яке задовільняє наступним умовам:
,
яке задовільняє наступним умовам:
1)(х,у)=(у,х);
2)(х+у,z)=(x,z)+(y,z);
3)
для
довільного дійсного числа
![]() і довільних
і довільних![]() виконується рівність
(х,у)=(х,у);
виконується рівність
(х,у)=(х,у);
4)(х,х)0 причому (х,х)=0 тоді і тільки тоді коли х=.
Число (х,у) називають скалярним добутком елементів х і у. З означення скалярного добутку випливає:
![]() ,
,
![]() .
.
Позначимо
![]() .
Пізніше ми покажемо, що ця величина
задовольняє всім умовам норми.
.
Пізніше ми покажемо, що ця величина
задовольняє всім умовам норми.
Теорема
3.1. Нехай
Х
– лінійна
система , на якій введено скалярний
добуток. Тоді для будь-яких
![]() і
і![]() має місце нерівність
має місце нерівність
![]() (3.1)
(3.1)
Нерівність (3.1) називається нерівністю Коші-Буняковського.
Доведення.
Якщо
![]() ,
то нерівність (3.1) очевидна.
,
то нерівність (3.1) очевидна.
Розглянемо
випадок, коли
![]() .
Нехай
.
Нехай![]() ,
очевидно,
,
очевидно,![]() .
Розглянемо скалярний добуток
.
Розглянемо скалярний добуток![]() деλ
–
довільне
дійсне число. Внаслідок означення
скалярного добутку (умова 4)
деλ
–
довільне
дійсне число. Внаслідок означення
скалярного добутку (умова 4)
![]() при довільному
при довільному![]() .
Перетворивши вираз, який стоїть в лівій
частині нерівності одержимо:
.
Перетворивши вираз, який стоїть в лівій
частині нерівності одержимо:![]() ,
або
,
або![]() .
Оскільки квадратний тричлен при всіх
дійсних
.
Оскільки квадратний тричлен при всіх
дійсних![]() невідє’мний, то дискримінант цього
тричлена недодатній, тобто
невідє’мний, то дискримінант цього
тричлена недодатній, тобто![]() звідси і слідує нерівність (3.1).
звідси і слідує нерівність (3.1).
Покажемо,
що величина
![]() є нормою. Виконання умови
є нормою. Виконання умови![]() ,
очевидне. Причому
,
очевидне. Причому![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли![]() .
Це слідує із умови 4) означення скалярного
добутку. З рівності
.
Це слідує із умови 4) означення скалярного
добутку. З рівності![]() ,
де
,
де![]() – дійсне число, слідує, що
– дійсне число, слідує, що![]() .
Переконаємось, що
.
Переконаємось, що![]() .
Так, як
.
Так, як![]() ,
,
то
внаслідок нерівності (3.1) маємо:
![]() .
Звідси слідує:
.
Звідси слідує:
![]() .
Нерівність
доведена.
.
Нерівність
доведена.
Таким
чином ми бачимо, що лінійна система, на
якій введено скалярний добуток, стає
лінійним нормованим простором, якщо
норму визначити рівністю
![]() ,
а значить і метричним, якщо за відстань
між елементамих
і у
прийняти величину
,
а значить і метричним, якщо за відстань
між елементамих
і у
прийняти величину
![]() .
.
§ 4. Приклади метричних просторів
I.
Простір Rn.
Розглянемо множину, елементами якої є
упорядковані набори n
дійсних чисел
![]() .
Якщо суму
.
Якщо суму![]() елементів
елементів![]() і
і![]() визначимо рівністю
визначимо рівністю![]() ,
а добуток
,
а добуток![]() ,
де
,
де![]() – рівністю
– рівністю![]() ,
і за нульовий елемент приймемо
,
і за нульовий елемент приймемо![]() ,
то дана множина стане лінійною системою.
Введемо скалярний добуток елементівх і
у
формулою:
,
то дана множина стане лінійною системою.
Введемо скалярний добуток елементівх і
у
формулою:
![]() (4.1).
(4.1).
Покажемо, що при цьому виконуються всі умови скалярного добутку.
1)![]() – очевидно.
– очевидно.
2)![]() .
.
3)Нехай
![]() ,
,![]() ,
,![]() .
Тоді
.
Тоді
![]() .
.
4)Для
довільного х
із даної множини маємо
![]() .
Звідси робимо висновок:
.
Звідси робимо висновок:
![]() ,
причому
,
причому
![]() тоді і тільки тоді, коли всі
тоді і тільки тоді, коли всі![]() .Таким
чином формула (4.1) визначає скалярний
добуток.
.Таким
чином формула (4.1) визначає скалярний
добуток.
Ввівши
норму на даній лінійній системі формулою
![]() ,
ми одержуємо лінійний нормований
простір.
,
ми одержуємо лінійний нормований
простір.
Тепер
можна ввести відстань між елементами
таким чином:
![]() .
.
Означення
4.1. Простір,
елементами якого є упорядковані набори
п дійсних
чисел
![]() ,
а відстань між елементами
,
а відстань між елементами![]() ,
,![]() визначається рівністю
визначається рівністю![]() ,
називаєтьсяпростором
,
називаєтьсяпростором
![]() .
.
II.
Простір l2.
Розглянемо
множину елементами якої є послідовності
дійсних чисел
![]() таких, що
таких, що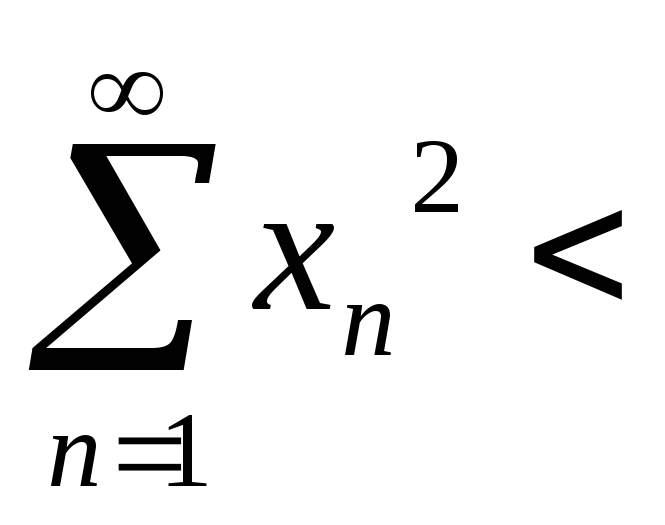
![]() .
.
Введемо
суму елементів
![]() і
і![]() таким чином:
таким чином:
![]() .
Покажемо, що
.
Покажемо, що![]() належить цій множині, тобто
належить цій множині, тобто![]() .
Так, як при кожномуп
виконується нерівність
.
Так, як при кожномуп
виконується нерівність
![]() і кожний із рядів
і кожний із рядів![]() ;
;
![]() збіжний, то на основі ознаки порівняння
збіжності додатніх рядів, ряд
збіжний, то на основі ознаки порівняння
збіжності додатніх рядів, ряд
![]() теж збіжний, тобтох+у
належать даній множині.
теж збіжний, тобтох+у
належать даній множині.
Якщо
за добуток дійсного числа
![]() на елементх
із цієї множини приймемо послідовність
на елементх
із цієї множини приймемо послідовність
![]() ,
а за нульовий елемент приймемо
,
а за нульовий елемент приймемо![]() ,
то дана множина стане лінійною системою.
Введемо скалярний добуток елементів
,
то дана множина стане лінійною системою.
Введемо скалярний добуток елементів![]() і
і![]() формулою
формулою
![]() (4.2).
(4.2).
Покажемо,
що ряд, який стоїть в лівій частині
рівності (4.2) є збіжний. З нерівності
![]() вірній при кожному
вірній при кожному![]() ,
на основі ознаки порівняння збіжності
додатніх рядів, слідує абсолютна
збіжність цього ряду. Виконання умов
скалярного добутку перевіряється так
само, як і в попередньому пункті.
,
на основі ознаки порівняння збіжності
додатніх рядів, слідує абсолютна
збіжність цього ряду. Виконання умов
скалярного добутку перевіряється так
само, як і в попередньому пункті.
Введемо норму:
![]() (4.3).
(4.3).
Таким
чином дана лінійна система є нормованим
лінійним простором, а значить і метричним,
якщо за відстань між
![]() і
і![]() прийняти:
прийняти:
![]() (4.4).
(4.4).
Означення
4.2.
Простір,
елементами якого є послідовності
![]() дійсних чисел, які задовольняють умову
дійсних чисел, які задовольняють умову![]() ,
а відстань між елементами
,
а відстань між елементами![]() і
і![]() визначається формулою
визначається формулою![]() називається
простором
називається
простором
![]() .
.
III.Простір
С[а,в]. Розглянемо множину функцій
неперервних на сегменті [а,в].
Якщо під сумою двох функцій розуміти
звичайну суму функцій, під добутком
числа
![]() на функцію
на функцію![]() ,
звичайний добуток числа на функцію, а
за нульовий елемент прийняти функцію
тотожньо рівну нулю, то дана множина
стає лінійною системою. Введемо на цій
системі норму рівністю:
,
звичайний добуток числа на функцію, а
за нульовий елемент прийняти функцію
тотожньо рівну нулю, то дана множина
стає лінійною системою. Введемо на цій
системі норму рівністю:
![]() (4.5)
(4.5)
Вираз в правій частині існує для будь-якої функції з даної множини внаслідок 2-ї теореми Вейєрштрасса.
Покажемо, що виконуються умови 1)-3) означення норми.
1.Нерівність
![]() , причому
, причому![]() ,
тоді і тільки тоді коли
,
тоді і тільки тоді коли![]() очевидна.
очевидна.
2.![]() .
.
3.Поскільки
при кожному
![]() виконується нерівність
виконується нерівність![]() ,
то і
,
то і
![]() ,
або те саме, що
,
або те саме, що![]() .
.
Таким чином наша лінійна система стає нормованим простором, якщо норму визначити рівністю (4.5), а значить і метричним, якщо відстань між точками х, у цього простору визначити формулою
![]() (4.6).
(4.6).
Означення
4.3. Простір
елементами якого є функції неперервні
на сигменті
![]() і відстань визначається формулою (4.6)
називаєтьсяпростором
і відстань визначається формулою (4.6)
називаєтьсяпростором
![]() .
.
