§ 2. Деякі відомості з теорії квадратичних форм

В цьому параграфі ми розглянемо деякі питання теорії квадратичних форм, які нам будуть потрібні надалі.

Означення 2.1 Функція

, а_іk=а_kі=сonst, (2.1),

яка залежить від змінних h₁, h₂,…, h_n, називається квадратичною формою від вказаних змінних.

Означення 2.2 Квадратична форма називається додатньо визначеною (від’ємно визначеною), якщо при будь-яких значеннях h₁, h₂,…, h_n, одночасно не рівних нулю, вона набуває додатніх (від’ємних) значень.

Додатньо визначені та від’ємно визначені форми називаються знаковизначеними.

Означення 2.3 Квадратична форма називається знакозмінною, якщо вона приймає як додатні так і від’ємні значення.

Означення 2.4 Квадратична форма називається квазізнаковизначеною, якщо вона приймає лише недодатні або лише невід’ємні значення, але при цьому вона дорівнює нулю при деяких h₁, h₂,…, h_n, які одночасно не дорівнюють нулю.

Сформулюємо критерій Сільвестера знаковизначеності квадратичних форм.

Симетричну матрицю будемо називати матрицею квадратичної форми (2.1). ВизначникиА₁=а₁₁, ,...,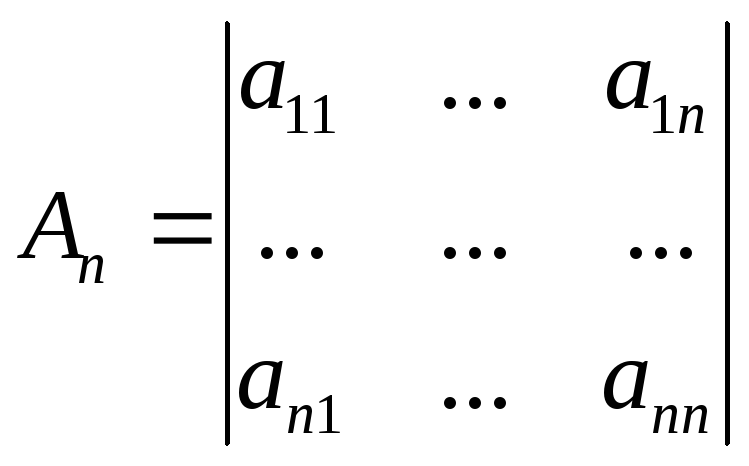називаються головними мінорами матриціА квадратичної форми.

Теорема 2.1 Для того, щоб квадратична форма (2.1) була додатньо визначеною необхідно і достатньо, щоб виконувалися нерівності:

А₁>0, A₂>0,…, A_n>0 (2.2).

Для того, щоб квадратична форма була від’ємно визначеною необхідно і достатньо, щоб знаки головних мінорів А₁, А₂,..., А_п чергувалися, причому А₁>0.

Очевидно диференціал другого порядку функції U=f(x₁, x₂,…,x_n) в точці М₀(х⁽⁰⁾₁,...,х⁽⁰⁾_п) є квадратичною формою змінних х₁, х₂,...,х_п.

Для формулювання достатніх умов існування екстремуму функції багатьох змінних використовуються квадратичні форми.

§ 3. Достатні умови існування екстремуму

Розглянемо достатні умови існування екстремуму.

Теорема 3.1 Нехай функція U=f(x₁, x₂,…, x_n) має в деякому околі стаціонарної точки М₀ частинні похідні до 2-го порядку включно, причому вони неперервні в точці М₀. Тоді, якщо в точці М₀ диференціал 2-го порядку цієї функції є знаковизначеною квадратичною формою, то в цій точці функція має екстремум: максимум, якщо ця форма від’ємно визначена та мінімум, якщо-додатньо визначена. Якщо диференціал 2-го порядку в цій точці є знакозмінною квадратичною формою, то екстремуму в точці М₀ немає.

Доведення. З умови теореми маємо, що наша функція двічі диференційовна в деякому околі точки М₀. Тому для будь-якої точки М з цього околу за формулою Тейлора матимемо, що

,

при цьому , N – проміжна точка з координатами N=(x⁽⁰⁾₁+₁x₁; x⁽⁰⁾₂+₂x₂,…, x⁽⁰⁾_n+_nx_n), де 0<₁<1,…,0<_n<1.

,

де , коли (х₁,...,х_п)(0,...,0).

Нехай тоді

.

Розглянемо поведінку множника в другому доданку при ²: коли (х₁,...,х_п)(0,...0).

Таким чином , де()0, коли 0.

Отже ми тільки що довели, що для будь-якої точки М справедлива рівність:

(3.1).

Перетворимо перший доданок останньої рівності:

=,

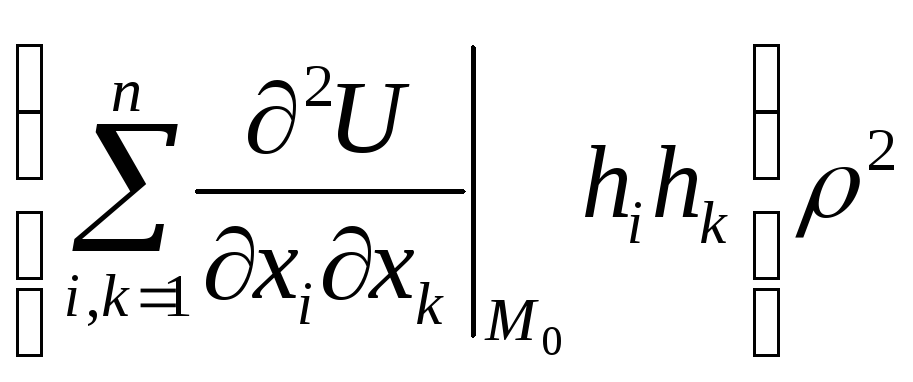де ,h_i1 і h₁²+…+h_n²=1.

Звідси і з (3.1) будемо мати:

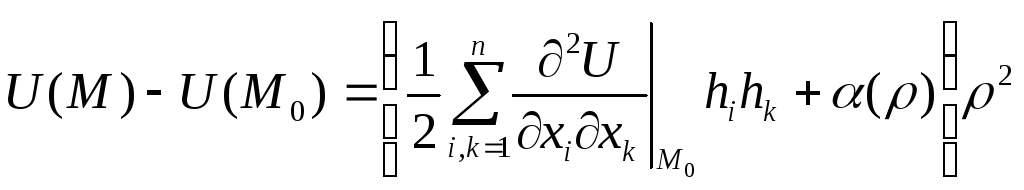(3.2).

Нехай диференціал 2-го порядку в точці М₀ є додатньо визначеною квадратичною формою. Оскільки диференціал 2-го порядку в точці М₀ дорівнює добутку першого доданка справа в (3.2) без множника , то цей доданок теж є додатньо визначеною квадратичною формою заданою на одиничній сфері просторуRⁿ. Оскільки ця квадратична форма є функцією неперервною на цій точці, а сфера Rⁿ є компактом (бо вона замкнена і обмежена) то за теоремою Вейєрштрасса на цій сфері знайдеться точка (h₁⁽⁰⁾,…,h_n⁽⁰⁾) в якій ця квадратична форма приймає найменше значення . Оскільки форма додатньо визначена, то 0. Отже перший доданок справа в (3.2) завжди більший або рівний /2. Оскільки ()0 коли 0 то знайдеться ₁>0: ₁ матимемо: ()</4.

Візьмемо . Тоді будемо мати .

Отже ми довели, що U(M)>U(M₀) для будь-якої точки М з ₁-околу точки М₀, а це означає, що в точці М₀ функція має мінімум (для максимуму доведення аналогічне).

Розглянемо доведення 2-ї частини теореми. Для цього зробимо кілька зауважень відносно квадратичної форми.

Якщо Ф(t₁,…,t_n) деяка знакозмінна квадратична форма, то можна підібрати дві точки h=(h₁,…,h_n), h=(h₁,…,h_n) такі, що h_i1; h_i1, ; h₁ ²+…+h_n ²=1; h₁ ²+…+h_n ²=1 і Ф(h)>0, Ф(h)<0. Дійсно, оскільки Ф знакозмінна квадратична форма, то знайдуться дві точки t=(t₁,…,t_n), t=(t₁,..,t_n): Ф(t)>0, Ф(t)<0. Покладемо

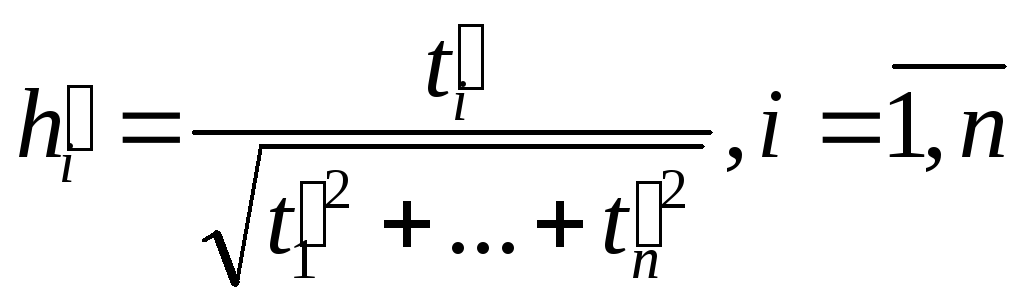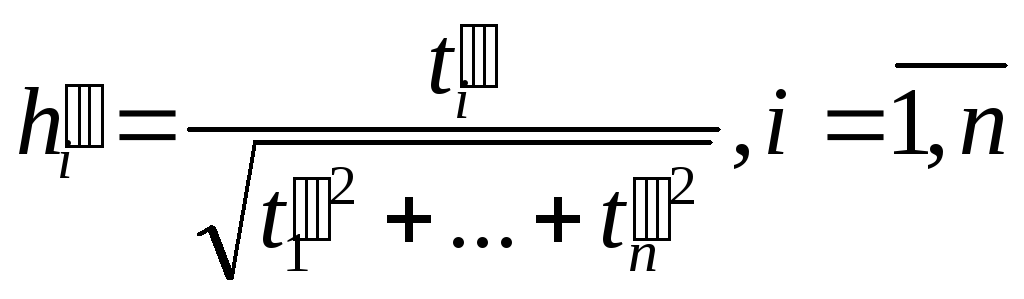, , ми одержимоh і h такі, що задовольняють умови і ;.

Візьмемо довільне >0. Нехай h=(h₁,…,h_n) така точка на одиничній сфері, що . Візьмемо точку таку, що, а значить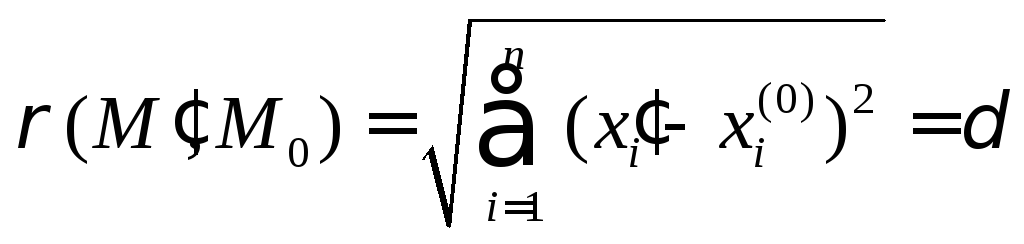. Тоді

_.

Оскільки ()0, коли 0, а перший доданок є додатнім і не залежить від , то можна підібрати  настільки малим, що вираз в дужках зберігатиме знак першого доданка. Тобто ми в як завгодно малому околі точки М₀, знайшли точку М, таку що U(M)-U(M₀)>0. Провівши аналогічні дослідження для U(M)-U(M₀), ми отримаємо, що в як завгодно малому околі точки М₀ знайдеться точка М , значення функції в якій менше за значення в точці М₀. Отже в точці М₀ функція не має екстремуму. Теорему доведено.

Часто виникає потреба дослідити на екстремум функцію двох змінних. Розглянемо цей випадок.

Теорема 3.2 (Достатні умови існування екстремуму для функції 2-х змінних). Нехай функція U=f(x;y) має частинні похідні другого порядку в деякому околі стаціонарної точки М₀, які неперервні в цій точці. Нехай а₁₁=f_xx(M₀); а₂₂=f_yy(M₀); а₁₂=f_xy(M₀) і (М₀)=а₁₁а₂₂-а₁₂². Якщо (М₀)>0, то в точці М₀ функція U має екстремум, а саме мінімум, коли а₁₁>0 і максимум, коли а₁₁<0. Якщо (М₀)<0 то екстремуму в точці М₀ дана функція немає.

Доведення. Перша частина теореми слідує з теореми 3.1 і критерію Сільвестера знаковизначеності квадратичної форми, бо А₁=а₁₁, А₂=а₁₁а₂₂-а₁₂². Тому, якщо М₀>0, то d²U є знаковизначеною квадратичною формою, а саме, якщо а₁₁>0 додатньо визначеною і при а₁₁<0 – від’ємно визначеною. А значить, якщо а₁₁>0 функція має мінімум, а при а₁₁<0 – максимум.

Розглянемо випадок коли (М₀)<0. На основі доведеного в теоремі 3.1, квадратичну форму диференціала в точці М₀ можна записати у вигляді: Ф=(a₁₁h₁²+2a₁₂h₁h₂+a₂₂h₂²), де h₁²+h₂²=1. Покажемо, що в цьому випадку квадратична форма 2-го диференціала в точці М₀ є знакозмінною. Для цього достатньо знайти дві точки h=(h₁,h₂), h=(h₁,h₂) на одиничному колі такі, що в одній із них форма Ф буде додатньою, а в іншій – від’ємною величиною.

Нехай а₁₁0, тоді

Ф(h₁h₂)=1/a₁₁(a₁₁²h₁²+2a₁₁a₁₂h₁h₂+a₁₂²h₂²+a₁₁a₂₂h₂² -a₁₂²h₂²)=

=1/a₁₁((a₁₁h₁+a₁₂h₂)²+(а₁₁а₂₂-а₁₂²)h₂²)

Якщо h₁=1; h₂=0,то вираз в дужках додатній. Якщо візьмемо і , то одержимо точку, яка лежить на одиничному колі і для якої вираз в дужках є від’ємним. Отже наш диференціал 2-го порядку є знакозмінною квадратичною формою, коли а₁₁0.

У випадку, коли а₁₁=0, Ф(h₁,h₂)=(2a₁₂h₁h₂+a₂₂h₂²)=(2a₁₂h₁+a₂₂h₂)h₂. Підберемо h₁; h₂ так, щоб 2а₁₂h₁>a₂₂h₂, h₁²+h₂²=1. Тоді величини 2а₁₂h₁+a₂₂h₂ і 2a₁₂h₁+a₂₂(-h₂) матимуть один і той самий знак, а значить (2a₁₂h₁+a₂₂h₂)h₂ і (2a₁₂h₁+a₂₂(-h₂))(-h₂) матимуть різні знаки. Це означає, що квадратична форма не є знаковизначеною. На основі попередньої теореми екстремуму в точці М₀ немає. Теорему доведено.