
- •Міністерство освіти і науки україни
- •Частина I Елементи функціонального аналізу Розділ 1. Метричні простори § 1. Поняття метричного простору
- •§ 2. Нормований метричний простір
- •§ 3. Скалярний добуток
- •§ 4. Приклади метричних просторів
- •Розділ 2. Збіжність в метричних просторах § 1. Границя послідовності
- •Нехай маємо послідовність
- •§ 2. Збіжність в просторах Rn, l2, c[a;b]
- •Розділ 3. Відкриті і замкнені множини § 1. Деякі поняття теорії метричних просторів
- •§ 2. Замикання і його властивості
- •§ 3. Замкнені множини і їх властивості
- •§ 4. Відкриті множини і їх влативості
- •Розділ 4. Неперервні відображення § 1. Поняття функції
- •§ 2. Границя і неперервність функції
- •§ 3. Зв’язні множини. Збереження зв’язності при неперервних відображеннях
- •Розділ 5. Компактні множини § 1. Компакти і їх властивості
- •§ 3. Критерій компактності
- •§ 4. Властивості функцій неперервних на компакті
- •Розділ 6. Повні метричні простори § 1. Приклади повних метричних просторів
- •§ 2. Властивості повних метричних просторів
- •§ 3. Теорема Банаха
- •Частина II Диференціальне числення функцій багатьох змінних Розділ 1. Поняття дійсної функції багатьох змінних
- •Розділ 2. Диференційовність функцій багатьох змінних § 1. Поняття диференційовної функції. Часткові похідні. Необхідні умови диференційовності
- •§ 2. Достатні умови диференційовності функції багатьох змінних
- •§ 3. Диференційовність складної функції.
- •§ 4. Інваріантність форми диференціала функції багатьох змінних.
- •§ 5. Похідна за напрямком. Градієнт.
- •Розділ 3. Частинні похідні і диференціали вищих порядків § 1. Частинні похідні вищих порядків
- •§ 2. Достатні умови незалежності змішаних частинних похідних від порядку диференціювання.
- •§ 3. Диференціали вищих порядків
- •§ 4. Формула Тейлора для функцій багатьох змінних
- •Розділ 4. Неявні функції § 1. Існування неявної функції однієї змінної
- •§ 2. Існування неявної функції багатьох змінних
- •§ 3. Існування неявної функції, яка задається системою рівнянь
- •Розділ 5. Екстремуми функцій § 1. Поняття екстремума функцій багатьох змінних
- •§ 2. Деякі відомості з теорії квадратичних форм
- •§ 3. Достатні умови існування екстремуму
- •§ 4. Умовний екстремум
- •Частина III. Розробка електронного посібника “Елементи функціонального аналізу та диференціальне числення функцій багатьох змінних”
- •Програмне середовище підручника
- •Як працювати з підручником?
- •Висновки
- •Часть II.– м.: ”Наука”, 1993. – 448с.
§ 2. Існування неявної функції багатьох змінних
У цьому параграфі ми розглянемо узагальнення вище доведеної теореми для випадку функції двох змінних.
Теорема 2.1 НехайМ0(х0,у0,z0)R3іF(x,y,z)такі, що
1) F(x0,y0,z0)=0;
2) в деякому околі точки М0, функціяF(x,y,z)іFx; Fy;Fz неперервні;
3) Fz(x0,y0,z0)0.
Тоді в деякому паралелепіпеді П={x,y,z: x0-1<x<x0+1, y0-2<y<y0-2,
z0-3<z<z0+3} рівнянняF(x,y,z)визначатиме єдину функціюz=F(x,y),яка буде визначена в прямокутнику П1={(х,у): x0-1<x<x0+1, y0-2<y<y0-2}, яка буде неперервно диференційовною в цьому прямокутнику.
Частинні похідні будуть обчислюватися за формулами:
![]() ;
;
![]()
Аналогічна теорема має місце для випадку функції від більше ніж 3-х змінних.
§ 3. Існування неявної функції, яка задається системою рівнянь
Іноді буває, що неявні функції задаються системою рівнянь. При цьому має місце така теорема.
Теорема
3.1 Нехай маємо таку систему:
 (3.1)
(3.1)
і![]() –
точка, координати якої задовільняють
кожному рівнянню системи (3.1).
–
точка, координати якої задовільняють
кожному рівнянню системи (3.1).
Тоді, якщо:
1) в
деякому околі точки М0, існують
всі часткові похідні першого порядку
функційF1,…,Fm,при
чому частинні похідні![]() ,
де
,
де![]() ;
;![]() ,
будуть неперервні в точціМ0;
,
будуть неперервні в точціМ0;
2) величина, яка називається якобіяном і позначається
 відмінна
від нуля в точціМ0,то
існують додатні числа1>0,
2>0,…,m>0та окіл точки
відмінна
від нуля в точціМ0,то
існують додатні числа1>0,
2>0,…,m>0та окіл точки
![]() такий, що в ньому існує єдиний набір
функцій:
такий, що в ньому існує єдиний набір
функцій:
U1=1(x1,…,xn)
U2=2(x1,…,xn)
………………..
Um=2(x1,…,xn),
які є розв’язками системи (3.1). В межах цього околу матимуть місце нерівності:
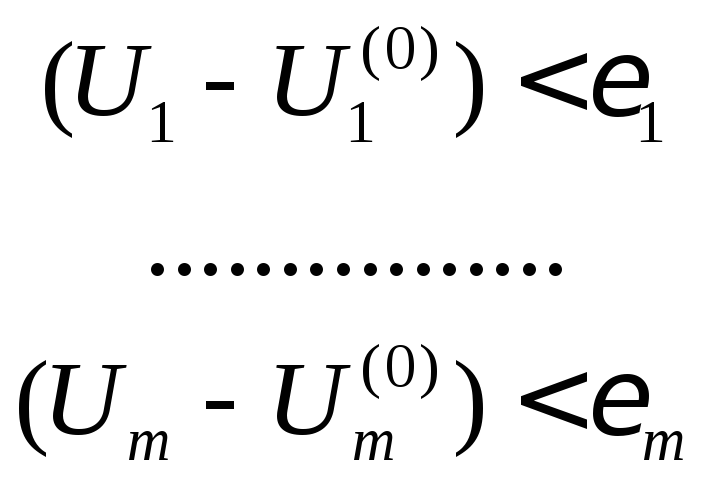
Кожна з функцій іє неперервною в цьому околі точкиМ0 та диференційовною в ньому.
В зв’язку з цією теоремою виникає питання, а як же знайти частинні похідні від функцій і, які одержалися в попередній теоремі. Адже із формулювання зрозуміло, що теорема стверджує тільки існування тих функцій і не дає можливості їх явно задати. Отже, як знайти їх частинні похідні?
Для цього продиференціюємо кожне із рівнянь системи (3.1) по змінній х1.Зважаючи на те, щохі – незалежні змінні, аUi– функції відх1...хп, матимемо:
![]()
![]()
……………………………………………
![]()
Ми одержимо
систему m лінійних
рівнянь відноснот невідомих![]() .
Головний визначник цієї системи це є
якобіян, взятий в точціМ0,
який за умовою теореми не дорівнює нулю.
.
Головний визначник цієї системи це є
якобіян, взятий в точціМ0,
який за умовою теореми не дорівнює нулю.
Розв’язавши
цю систему, ми знайдемо
![]()
Для того, щоб знайти частинні похідні по інших змінних зробимо те саме.
Розділ 5. Екстремуми функцій § 1. Поняття екстремума функцій багатьох змінних
Нехай функція U=f(x1,x2,…,xn) задана на множині ЕRп.
Означення
1.1 Будемо
говорити, що в точці
![]() функція
маємаксимум,
якщо існує окіл цієї точки такий, що для
будь-яких точок М
із цього околу, які належать множині Е,
виконується нерівність: f(M)≤f(M0).
функція
маємаксимум,
якщо існує окіл цієї точки такий, що для
будь-яких точок М
із цього околу, які належать множині Е,
виконується нерівність: f(M)≤f(M0).
Означення
1.2 Будемо
говорити, що в точці
![]() функція маємінімум,
якщо існує окіл цієї точки такий, що для
будь-яких точок М
із цього околу, які належать множині Е,
виконується нерівність: f(M)≥f(
функція маємінімум,
якщо існує окіл цієї точки такий, що для
будь-яких точок М
із цього околу, які належать множині Е,
виконується нерівність: f(M)≥f(![]() M0).
M0).
Як і в одномірному випадку точки максимуму та мінімуму функції називають точками екстремуму.
Теорема 1.1. (Необхідні умови існування екстремуму).
Нехай
функція U=f(x1,…xn),
яка задана в області D,
має в точці
![]() екстремум.
Якщо в цій точці існують всі її частинні
похідні 1-го порядку, то всі вони дорівнюють
нулю:
екстремум.
Якщо в цій точці існують всі її частинні
похідні 1-го порядку, то всі вони дорівнюють
нулю:
![]() .
.
Доведення.
Нехай дана функція в даній точці має
максимум. Тоді функція
![]() ,
як функція від однієї змінної пох1
,
як функція від однієї змінної пох1![]() має
в точці х01
теж максимум, причому похідна в цій
точці дорівнює частинній похідній
має
в точці х01
теж максимум, причому похідна в цій
точці дорівнює частинній похідній
![]() .
Оскільки функція має похідну в цій точці
і ця точка є для неї точкою максимуму,
то за відомою теоремою з одномірного
аналізу її похідна, а отже і
.
Оскільки функція має похідну в цій точці
і ця точка є для неї точкою максимуму,
то за відомою теоремою з одномірного
аналізу її похідна, а отже і
![]() ,
аналогічно і з всіма іншими частинними
похідними.
,
аналогічно і з всіма іншими частинними
похідними.
Аналогічно доводиться теорема, коли функція має мінімум.
Теорему доведено.
Означення
1.3 Точку
М0,
в якій всі частинні похідні функцій
![]() ,
або не існують, називають критичною
точкою цієї функції.
,
або не існують, називають критичною
точкою цієї функції.
Точки в яких всі частинні похідні 1-го порядку дорівнюють нулю, називають ще й стаціонарними.
Таким чином, щоб функція мала екстремум в даній точці необхідно, щоб ця точка була критичною. Наступний приклад показує, що це не є достатньою умовою.
Розглянемo функцію z=xy. Точка (0,0) тут є критичною, але в ній екстремуму немає. Бо який би ми окіл не взяли, в ньому існують точки в яких значення функції більші від значень функції в точці (0,0) та існують точки, в яких значення функції менші.
