Розділ 2. Диференційовність функцій багатьох змінних § 1. Поняття диференційовної функції. Часткові похідні. Необхідні умови диференційовності

Очевидно є проблема перенесення означення похідної функції однієї змінної на похідну функції багатьох змінних. І ця проблема полягає в тому, що кожна із змінних має свій приріст.

В зв’язку з цим, перенести означення похідної можна, якщо приріст надавати не всім змінним, а тільки одній із них. В результаті ми одержимо аналог похідної, який будемо називати частковою похідною від функції багатьох змінних, як було в одномірному аналізі.

Означення 1.1. Величину , називають частковим приростом функціі по змінній х_і, де х_і0, в точці х⁽⁰⁾.

Означення 1.2. Якщо існує границя 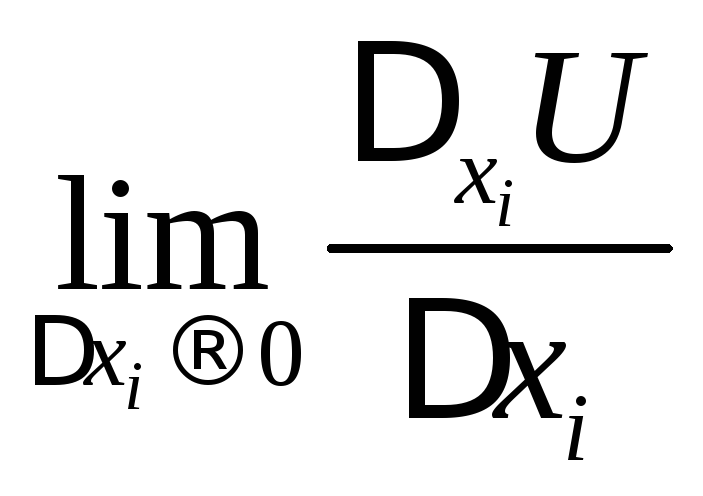, то її називають частинною похідною функції U(x) в точці х⁽⁰⁾ і позначають: , або .

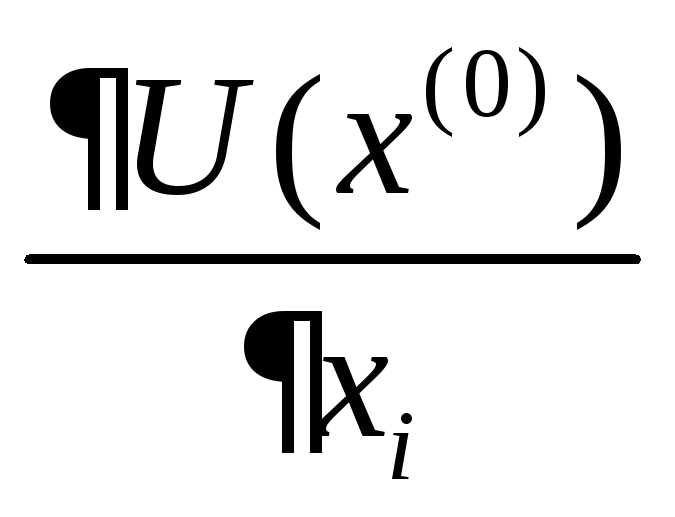Означення 1.3. Функція U=f(x), називається диференційовною в точці х⁽⁰⁾, якщо повний приріст цієї функції в цій точці можна зобразити у вигдяді , (1.1),

де А_і – незалежні від величини, _і є функціями від , які прямують до нуля, коли .

Означення 1.4. Якщо функція диференційовна в точці х₀, то вираз називається диференціалом функції в даній точці і позначається ,

.

Як ми бачимо, диференціал це є лінійна відносно частина приросту функції. З рівності (1.1) слідує, що якщо функція диференційовна в точці , то вона неперервна в цій точці.

Теорема 1.1. Якщо функція диференційовна в точці, то існують усі часткові похідні в цій точці.

Якщо рівність (1.1) справедлива для будь-якого приросту х⁽⁰⁾, то вона справедлива, коли , а решта . Тоді , поділимо обидві частини на . Після переходу до границі, одержимо: .

Обернене твердження взагалі невірне.

Розглянемо функцію

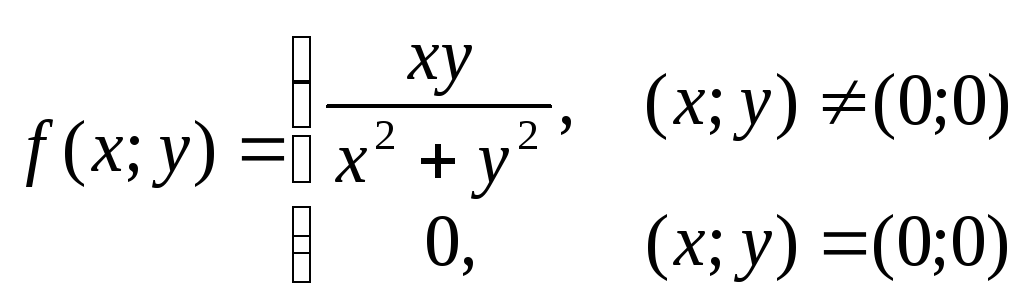
В точці (0;0) існують часткові похідні.

;

.

Але дана функція не є неперервною в точці (0;0), тому вона не може бути і диференційовною в цій точці.

Таким чином цей приклад показує:

1)Із існування всіх часткових похідних в точці, не випливає диференційовність цієї функції в цій точці.

2)Не обов’язково розривна функція не повинна мати часткових похідних.

Зауважимо, що в означенні диференційовної функції на накладається умова: .

З теореми 1.1. бачимо, що якщо функція диференційовна в точці х₀, то її приріст можемо записати у вигляді

, де _і – нескінченно малі функції від .

Якщо – незалежні змінні, то їх прирости називаються диференціалами, тобто: .

Таким чином диференціал функції можна записати у вигляді .

Як ми знаємо, між диференційовністю функції однієї змінної в якійсь точці х₀ і наявністю дотичної до графіка функції в точці (х₀, f(x₀)), є зв’язок. Перенести його на функцію будь-якої кількості змінних (3) – не можливо, бо графік такої функції буде розміщуватись в просторі розмірності >3. Та все ж таки для функції z=f(x;y) таку проблему можна ставити, бо її графіком буде деяка поверхня в просторі R³, для якої ми можемо ввести поняття дотичної площини, а отже, можливо, і зможемо зв’язати проблему існування дотичної площини з умовою диференційовності функції.

Означення 2.4. Площина Р, називається дотичною до деякої поверхні G в деякій точці М₀(у₀; x₀; z₀) цієї поверхні, якщо:

1) М₀Р;

2) кут між цією площиною і січною М₀М, де М – будь-яка точка поверхні G, прямує до нуля, якщо точка М прямує до співпадання з точкою М₀.

Нехай функція z=f(x; y) диференційовна в точці А(х₀; y₀), тоді приріст функції можна записати у вигляді , _, коли 0, де _.

Розглянемо площину: і покажемо, що вона є дотичною до поверхні в точці (х₀; y₀; z₀), де z₀=f(x₀; y₀). Для того, щоб довести, що ця площина буде дотичною до нашої поверхні в точці (х₀; y₀; z₀) потрібно показати:

1) що вона проходить через точку (х₀; y₀; z₀), а це очевидно, бо координати цієї точки наше рівняння задовільняють;

2) що кут між нормаллю цієї площини і січною прямуватиме до 90, коли точка М прямує до точки М₀, рухаючись по цій поверхні.

Нехай –- вектор нормалі до площини в точці М₀. Розглянемо вектор , де М(х; y; z) – довільна точка на поверхні.

Врахувавши, що , одержимо:

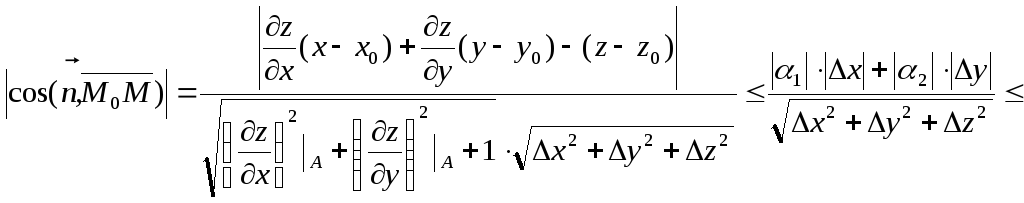
, коли ,

це рівнозначне тому, що коли ММ₀ по поверхні, то кут між і прямує до 90, а це означає, що кут між площиною і січною прямує до нуля.

Отже площина є дотичною до функції в точці М₀(х₀; y₀; z₀).