
- •Міністерство освіти і науки україни
- •Частина I Елементи функціонального аналізу Розділ 1. Метричні простори § 1. Поняття метричного простору
- •§ 2. Нормований метричний простір
- •§ 3. Скалярний добуток
- •§ 4. Приклади метричних просторів
- •Розділ 2. Збіжність в метричних просторах § 1. Границя послідовності
- •Нехай маємо послідовність
- •§ 2. Збіжність в просторах Rn, l2, c[a;b]
- •Розділ 3. Відкриті і замкнені множини § 1. Деякі поняття теорії метричних просторів
- •§ 2. Замикання і його властивості
- •§ 3. Замкнені множини і їх властивості
- •§ 4. Відкриті множини і їх влативості
- •Розділ 4. Неперервні відображення § 1. Поняття функції
- •§ 2. Границя і неперервність функції
- •§ 3. Зв’язні множини. Збереження зв’язності при неперервних відображеннях
- •Розділ 5. Компактні множини § 1. Компакти і їх властивості
- •§ 3. Критерій компактності
- •§ 4. Властивості функцій неперервних на компакті
- •Розділ 6. Повні метричні простори § 1. Приклади повних метричних просторів
- •§ 2. Властивості повних метричних просторів
- •§ 3. Теорема Банаха
- •Частина II Диференціальне числення функцій багатьох змінних Розділ 1. Поняття дійсної функції багатьох змінних
- •Розділ 2. Диференційовність функцій багатьох змінних § 1. Поняття диференційовної функції. Часткові похідні. Необхідні умови диференційовності
- •§ 2. Достатні умови диференційовності функції багатьох змінних
- •§ 3. Диференційовність складної функції.
- •§ 4. Інваріантність форми диференціала функції багатьох змінних.
- •§ 5. Похідна за напрямком. Градієнт.
- •Розділ 3. Частинні похідні і диференціали вищих порядків § 1. Частинні похідні вищих порядків
- •§ 2. Достатні умови незалежності змішаних частинних похідних від порядку диференціювання.
- •§ 3. Диференціали вищих порядків
- •§ 4. Формула Тейлора для функцій багатьох змінних
- •Розділ 4. Неявні функції § 1. Існування неявної функції однієї змінної
- •§ 2. Існування неявної функції багатьох змінних
- •§ 3. Існування неявної функції, яка задається системою рівнянь
- •Розділ 5. Екстремуми функцій § 1. Поняття екстремума функцій багатьох змінних
- •§ 2. Деякі відомості з теорії квадратичних форм
- •§ 3. Достатні умови існування екстремуму
- •§ 4. Умовний екстремум
- •Частина III. Розробка електронного посібника “Елементи функціонального аналізу та диференціальне числення функцій багатьох змінних”
- •Програмне середовище підручника
- •Як працювати з підручником?
- •Висновки
- •Часть II.– м.: ”Наука”, 1993. – 448с.
§ 4. Властивості функцій неперервних на компакті
Коли ми вивчали функції дійсної змінної, то ми бачили, що якщо функція неперервна на сегменті, то вона мала цілий ряд властивостей. Деякі з цих властивостей мають місце для функцій неперервних на компактах.
Нехай
маємо метричні простори Х
і У,
через
![]() будемо позначити відстань в Х,
будемо позначити відстань в Х,
![]() – відстань в
У;
КÌ
Х компакт
в Х.
– відстань в
У;
КÌ
Х компакт
в Х.
Теорема 4.1. Якщо функція f неперервна на компакті К, то образ f(К), цього компакта, є компактом.
Доведення.
Нехай f:KÌ
X®Y
неперервна функція на компакті К.
Через f(К)
позначимо образ К
при даному відрбраженні. Покажемо, що
f(К)
компакт. Нехай у1,
у2,...,
уп...
послідовність з f(К).
Через хп
позначимо![]() – прообраз
уп.
Якщо якась точка уп
має декілька прообразів, то будемо брати
будь-який з них. Таким чином ми отримали
послідовність {хп},
хп
є К. Так як
К
компакт, то з {хп}
можна виділити підпослідовність
– прообраз
уп.
Якщо якась точка уп
має декілька прообразів, то будемо брати
будь-який з них. Таким чином ми отримали
послідовність {хп},
хп
є К. Так як
К
компакт, то з {хп}
можна виділити підпослідовність
![]() ,
яка збігається до точки, яка належить
К.
Нехай
,
яка збігається до точки, яка належить
К.
Нехай
![]() ,
f(х0)=у0f(K).
Розглянемо
підпослідовність
,
f(х0)=у0f(K).
Розглянемо
підпослідовність
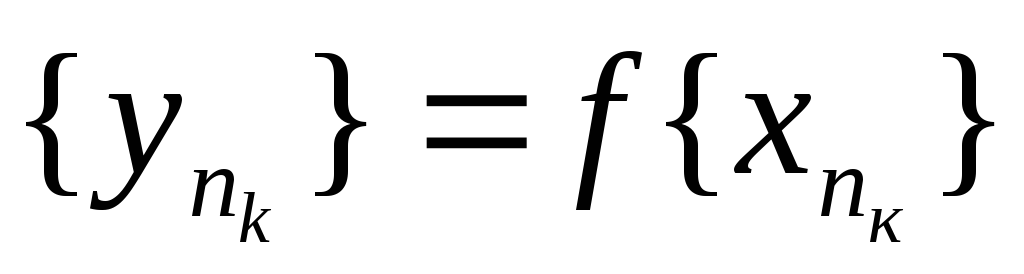 послідовності
{уп}.
Поскільки f
неперервна
в х0,
то
послідовності
{уп}.
Поскільки f
неперервна
в х0,
то
![]() .
Звідси й
слідує, що К
є компактом.
.
Звідси й
слідує, що К
є компактом.
Нехай
ЕÌ
Х, f:Е®У.
f(Е),
образ Е
при даному відображенні. Якщо виявиться,
що для кожного у
є f(Е)
існує тільки одне х
є Е таке, що
f(х)=у,
то на f(Е)
можна визначити функцію, яка кожному
уÎf(Е)
ставить у відповідність хÎЕ
таке, що f(x)=y.
Ця функція називається оберненою до f.
Позначають обернену функцію:
![]() .
Зрозуміло, що областю визначення
оберненої функції є f(E),
а областю
значень – Е.
При цьому f
є оберненою до
.
Зрозуміло, що областю визначення
оберненої функції є f(E),
а областю
значень – Е.
При цьому f
є оберненою до
![]() .
.
Очевидно, для того, щоб функція f мала обернену, тобто була оборотною, необхідно і достатньо, щоб відображення f:E®f(E) – було взаємно-однозначним.
Теорема
4.2. Якщо
функція f:KÌX®Y,
неперервна на компакті і відображення
f:K®f(K)
– взаємно-однозначне, то обернене
відображення
![]() -
неперервне
на f(K).
-
неперервне
на f(K).
Доведення.
Доведення проведемо методом від
супротивного. Припустимо, що
![]() не є
неперервною функцією на f(K).
Тоді існує y0Îf(K)
таке, що в ній
не є
неперервною функцією на f(K).
Тоді існує y0Îf(K)
таке, що в ній
![]() має розрив. Нехай f
-1(y0)=х0.
Оскільки f
-1
має розрив в точці у0,
то існує e
>0 таке, що
для кожного натурального п,
знайдеться упÎf(K)
таке, що
має розрив. Нехай f
-1(y0)=х0.
Оскільки f
-1
має розрив в точці у0,
то існує e
>0 таке, що
для кожного натурального п,
знайдеться упÎf(K)
таке, що
![]() ,
але
,
але
![]() .
Нехай хп=f
-1(уп),
хпÎК.
Так, як К
компакт, то з послідовності {xn}
можна виділити підпослідовність
.
Нехай хп=f
-1(уп),
хпÎК.
Так, як К
компакт, то з послідовності {xn}
можна виділити підпослідовність
![]() ,
яка збігається до точки із множини К,
,
яка збігається до точки із множини К,
![]() ,
з нерівності
,
з нерівності
![]() слідує
слідує
![]() ,
,
коли
![]() .
Звідси робимо висновок, що х0¹х*.
Внаслідок неперервності f
маємо
.
Звідси робимо висновок, що х0¹х*.
Внаслідок неперервності f
маємо
![]() (4.1)
(4.1)
(f(x*)¹y0,
так як
у0=f(x0),
а
відображення взаємно-однозначне).
З іншого боку
![]() ,
коли
,
коли
![]() ,
тобто
,
тобто
![]() ,
що суперечить (4.1). Теорему доведено.
,
що суперечить (4.1). Теорему доведено.
Теорема 4.3. Якщо функція f:KÌX®Y, неперервна на компакті К, то вона і рівномірно неперервна на К.
Доведення.
Доведення проведемо методом від
супротивного. Припустимо, що функція f
не є рівномірно неперервною на К.
Тоді існує e0>0
таке, що для кожного натурального п
знайдуться точки
![]() ,
які належать множині К
такі, що
,
які належать множині К
такі, що
![]() ,
але
,
але
![]() .
.
Одержали
дві послідовності
![]() .
Поскільки К
– компакт, то з
.
Поскільки К
– компакт, то з
![]() можна виділити підпослідовність
можна виділити підпослідовність
![]() ,
яка збігається до точки х0,
яка належить К.
Розглянемо підпослідовність
,
яка збігається до точки х0,
яка належить К.
Розглянемо підпослідовність
![]() послідовності
послідовності
![]() .
З нерівності
.
З нерівності
![]() слідує, що
слідує, що
![]() .
Так, як функція
f
неперервна в точці х0,
то
.
Так, як функція
f
неперервна в точці х0,
то
![]() і
і
![]() .
Тобто
.
Тобто
![]() =
=![]() (4.3).
(4.3).
З
нерівності
![]()
![]()
![]() робимо висновок, що
робимо висновок, що
![]() ,
що суперечить нерівності
,
що суперечить нерівності
![]() при всіх натуральних k.
Теорему доведено.
при всіх натуральних k.
Теорему доведено.
Розглянемо деякі властивості функцій неперервних на компакті, значення яких є дійсні числа, тобто f:KÌX®R (R – множина дійсних чисел). Такі функції називаються числовими.
Теорема 4.4. (Вейєрштрасса) Якщо числова функція неперервна на компакті КÌХ, то вона обмежена на К і приймає на ньому найбільше та найменше значення.
Доведення. Нехай f:KÌX®R є неперервною на К. Внаслідок Т.4.1, множина f(K) – компакт, а, оскільки, компакт є обмеженою множиною, то f(K) є обмеженою множиною.
Доведемо,
що функція приймає найбільше і найменше
значення на К,
тобто існують точки х1
і
х2
такі, що для всіх хÎК
виконується нерівність:
![]() .
Нехай
.
Нехай
![]() .
Візьмемо e
>0. Тоді
існує хК
таке, що
.
Візьмемо e
>0. Тоді
існує хК
таке, що![]() .
Звідси робимо висновок, що b
є точкою дотику f(K).
Внаслідок замкненості f(K)
(Т. 1.1), bÎf(K).
Значить існує х1ÎК,
що f(x1)=b.
.
Звідси робимо висновок, що b
є точкою дотику f(K).
Внаслідок замкненості f(K)
(Т. 1.1), bÎf(K).
Значить існує х1ÎК,
що f(x1)=b.
Аналогічно
показуємо, що існує х2ÎК
таке, що
f(x2)=а,
де
![]() .
Теорема доведена.
.
Теорема доведена.
