II семестр

1. Функции нескольких переменных.

2. Множества уровней.

3. Однородные функции.

4. Выпуклые и вогнутые функции.

5. Производственные функции.

6. Линии изоквант и изокост.

7. Предел функции в точке.

8. Непрерывность.

9. Свойства непрерывных функций.

10. Частные производные.

11. Примеры применения частных производных в экономике.

12. Дифференцируемость функции нескольких переменных.

13. Градиент функции и его свойства.

14. Производная функции по направлению.

15. Неявные функции.

16. Экстремумы функций нескольких переменных.

17. Необходимое условие экстремума.

18. Достаточные условия экстремума.

19. Задачи на условный экстремум.

20. Наибольшее и наименьшее значения функции.

21. Выравнивание эмпирических зависимостей.

22. Метод наименьших квадратов.

23. Первообразная функции и неопределенный интеграл.

Функция F(x) наз-ся первообразной ф-ции f(x) на определенном интервале, если F'(x)=f(x) или dF(x)=f(x)dx. Основная теорема интегрирования:

Если ф-ция f(x), определенная на интервале x , имеет 1 первообразную F(x), то она имеет бесконечное число первообразных, все они описываются выр-ем F(x)+c, где c-const. Док-во: По опр-ю F'(x)=f(x), (F(x)+c)'=F'(x)+(c)'=f(x). Докажем, что F(x)+c описывает все первообразные ф-ции f(x). Возьмем F1(x)- первообразная.Докажем, что (F1(x)-F(x))-есть константа. Обозначим F₁(x)-F(x)=r(x). Исследуем r'(x)= (F1(x)-F(x))'=F1'(x)-F'(x), т.к. F₁ и F - первообр. ф-ции f(x), то r'(x)=f(x)-f(x)≡0(≡ - это для любого x). Пусть x₁ и x₂ принадлежат X. Применим ф-лу Лагранжа для x₁ и x₂. Пусть x₁ < x₂, тогда r(x₂)-r(x₁)=r'(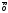*(x₂ - x₁), где r'(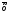)=0, х₁<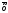<х₂. Значит r(x₂)-r(x₁)=0, значит r(x₂)=r(x₁), для разных аргументов ф-ция принимает равные значения, то ф-ция r(x) постоянна по опред-ю, значит r(x) - константа и F'(x)=F(x)+c. Ч.Т.Д. Неопределенный интеграл - совокупность всех первообразных для ф-ции f(x) на интервале X. 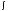f(x)dx=F(x)+c f(x)-подинтегральная ф-ция, f(x)dx- подинтегральное выражение.

24. Свойства неопределенного интеграла.

1) дифференциал от неопред-го интеграла = подынтегральному выраж-ю d(∫f(x)dx)=f(x)dx.

ДОК-ВО: в самом деле по ф-ле ∫f(x)dx=F(x)+C:

d(∫f(x)dx)=d(F(x)+C)=d(F(x))=f(x)dx.

2) неопред-й интергал от дифференциала некот. фун-и U(x) = самой этой фун-и + некот. константа.

∫dU(x)=U(x)+C.

ДОК-ВО: в кач-ве первообразной можно взять U(x). Согласно теореме интеграл = тогда U(x)+C.

3) неопред-й интеграл от алгебраич. выраж-я = алгебраич. сумме интегралов от слагаемых.

∫(f(x)+φ(х)-ψ(х))dx=∫f(x)dx+∫φ(х)dx-∫ψ(x)dx

ДОК-ВО: для того, чтобы док-ть данное рав-во надо док-ть рав-во двух бесконечных множеств фун-й. Пусть а – бесконечное множество фун-й левой части; в - -//-//- правой части. Множ-во а есть множ-во всех фун-й, дифференциал кот-х равен (f(x)+φ(x)+ψ(x))dx. Множ-во в – это множ-во всех фун-й, дифференциал кот-х равен f(x)dx+φ(x)dx-ψ(x)dx. Т.к. f(x)dx+φ(x)dx-ψ(x)dx=f(x)dx. => множ-во а и в равны, т.к. состоят из одних и тех же фун-й.

4) постоянный множитель можно выносить из под знака интеграла.

∫аf(x)dx=а∫f(x)dx

ДОК-ВО: для того, чтобы док-ть рав-во, достаточно проверить, что производные от его левой и правой частей совпадают. Диф-я левую и правую части получаем: ( ∫ аf(x)dx )′ = af(x) и (a∫f(x)dx+C)′ = a( ∫ f(x)dx)′ + (C)′ = af(x). А это значит рав-во справедливо.

5) если интеграл фун-и f(x)dx=F(x)+C, то ∫f(u)du=F(u)+C, где u – яв-ся некот. фун-ей от х.