1.2. Производная сложной функции

Пусть y=f(u), где и является не независимой переменной, а функцией не­зависимой переменной х: и=(х). Таким образом, у=f((х)).

В этом случае функция у называется сложной функ­цией х, а переменная и — промежуточным аргументом.

Производная сложной функции находится на основании следующей теоремы:

Теорема: Если у=f(и) и и=(х) – дифференцируемые функции своих аргументов, то производная сложной функции у=f((х)) существует и равна производной функции у по промежуточному аргументу и на производную промежуточного аргумента и по независимой переменной х:

Эта теорема распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.

Например, если у=f(и), и=(v), v=(x), т.е. у=f(((х))), то

1.3. Формулы дифференцирования

Во всех приведенных ниже формулах буквами и и v обозначены дифференцируемые функции независимой переменной х: и=и(х), v=v(x), а буквами а, с, п – постоянные:

1. 

2. 

3. 

4. 

5. 

6. .

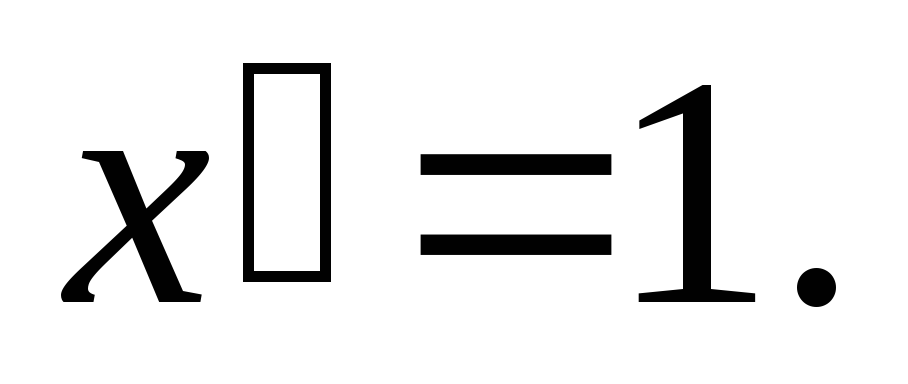
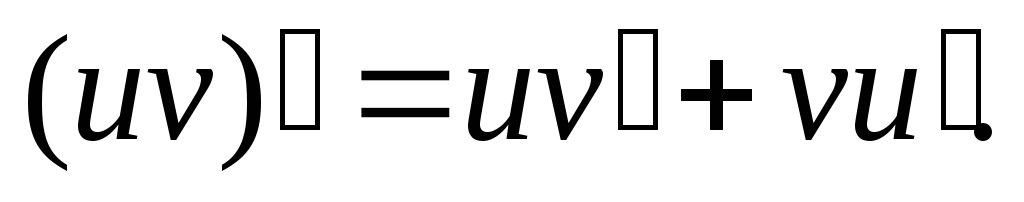
Остальные формулы написаны как для функций независимой переменной, так и для сложных функций:

7. 7а.

8. 8а.

9. 9а.

10. 10а.

11. 11а.

12. 12а.

13. 13а.

14. 14а.

15. (е^х)=е^х. 15а. (е^и)=е^ии.

16. 16а.

17. 17а.где а>0, а1.

При решении приведенных ниже примеров сделаны подробные записи. Однако следует научиться дифференцировать без промежуточных записей.

Пример 1. Найти производную функции у=5х³-2х+

Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3, 5, 7 и 8:

Пример 2. Найти производную функции

Решение. Применяя формулы 6, 3, 7 и 1, получим

Пример 3. Найти производную функции у=sin³ и вычислить ее значение при =/3.

Решение. Это сложная функция с промежуточным аргументом sin. Используя формулы 7а и 10, имеем

f () = 3 sin² (sin )=3 sin²  cos .

Вычислим значение производной при =/3:

Пример 4. Найти производную функции

Решение. Это сложная функция с промежуточным аргументом cos х. Применяя формулы 3, 5, 7а, 11, 16а, получим

Пример 5. Найти производную функции

Решение. Дифференцируем данную функцию по формулам 6, 12, 3 и 1:

Пример 6. Найти производную функции и вычислить ее значение приt=2.

Решение. Сначала преобразуем функцию, исполь­зуя свойства логарифмов:

Теперь дифференцируем по формулам 3, 16а, 7 и 1:

Вычислим значение производной при t=2:

Пример 7. Найти производную функции и вычислить ее значение прих=0.

Решение. Используем формулы 6, 3, 14а, 9а, 5 и 1:

Вычислим значение производной при х=0:

1.4. Геометрический смысл производной

Производная функции имеет простую и важную геометрическую ин­терпретацию.

Если функция y=f(x) дифференцируема в точке x, то график этой функции имеет в соответствующей точ­ке касательную, причем угловой коэффициент касатель­ной равен значению производной в рассматриваемой точке.

Угловой коэффициент касательной, проведенной к графику функции y=f{x) в точке (х₀, у₀), равен значе­нию производной функции при х=х₀, т.е. k_кас=у (х₀).

Уравнение этой касательной имеет вид:

у-у₀ = f (х₀) (х-х₀).

Пример 8. Составить уравнение касательной к гра­фику функции в точкеА(3, 6).

Решение. Для нахождения углового коэффициента касательной найдем производную данной функции:

Угловой коэффициент касательной равен значению производной функции при х=3:

k=у (3)=23²-23-2=18-6-2=10.

Уравнение касательной имеет вид

у-6 = 10 (х-3), или у-6 = 10х-30, т.е.

10х-у-24 = 0.

Пример 9. Составить уравнение касательной, проведенной к графику функции в точке с абсциссойх=2.

Решение. Сначала найдем ординату точки касания А (2, у). Так как точка А лежит на кривой, то ее коор­динаты удовлетворяют уравнению кривой, т. е.

А (2, 2).

Уравнение касательной, проведенной к кривой в точ­ке А (2, 2), имеет вид у-2 = k(x-2). Для нахождения углового коэффициента касательной найдем производ­ную:

Угловой коэффициент касательной равен значению производной функции при х=2:

Тогда уравнение касательной:

у-2 = - (х-2), у-2=-х+2, т. е. х+у-4 = 0.