15.5. Расчет коэффициентов активности ионов

Одним из важных следствий, вытекающих из основного уравнения, является возможность расчета коэффициентов активности ионов. Учитывая связь энергии межионного взаимодействия с коэффициентами активности (уравнение (15.36)), получаем:

. (15.58)

Подставим сюда значение из уравнения (15.46):

. (15.59)

В этом уравнении концентрация выражена числом ионов n_iв 1 см³раствора. Эта величина связана с молярной концентрациейc_i:, (где N_А– число Авогадро), тогда

. (15.60)

Преобразуем это уравнение, вводя в него ионную силу , переходя к десятичным логарифмам и обозначив

. (15.61)

После этих подстановок уравнение для коэффициентов активности ионов принимает вид:

. (15.62)

Уравнение Дебая – Гюккеля (15.62) дает возможность рассчитать коэффициенты активности отдельного вида ионов, но экспериментально можно определять лишь средние ионные коэффициенты активности. Поэтому для опытной проверки уравнения нужно перейти к средним ионным коэффициентам активности. Исходя из их определения (уравнение (15.24)), получим

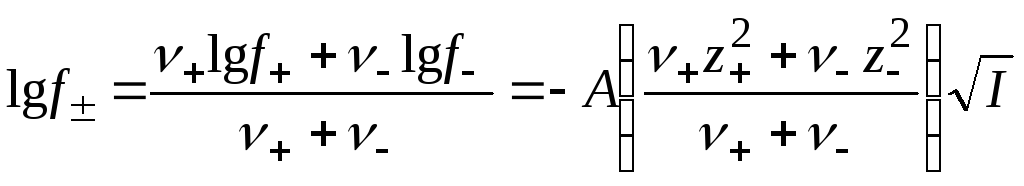. (15.63)

Учитывая, что система в целом электронейтральна, т.е. |₊z₊| = |_–z_–|, выражение в скобках представим в форме

(15.64)

и окончательно получаем

. (15.65)

Это уравнение совпадает с эмпирически установленной закономерностью и является теоретическим обоснованием правила ионной силы Льюиса – Рендалла. Экспериментальная проверка уравнения (15.65) показала, что оно справедливо только для разбавленных растворов электролитов (I0,01 – 0,02), при больших концентрациях наблюдаются значительные расхождения экспериментально определяемых величин с теоретически рассчитанными.

Ограниченность теории Дебая – Гюккеля предопределена, прежде всего, недостатками самой модели, использованной при создании теории.

Согласно модели, рассматривается только электростатическое межионное взаимодействие, которое вместе с тепловым движением приводит к образованию сферической ионной атмосферы. Это допущение справедливо только для разбавленных растворов. Увеличение концентрации приводит к уменьшению межионного расстояния, начинают проявляться силы межмолекулярного взаимодействия, например, силы Ван-дер-Ваальса, а размер ионной атмосферы становится соизмеримым с размерами самого иона. В этом случае уже нельзя рассматривать ионы как точечные заряды.

При расчетах используется разложение показательной функции в ряд с ограничением двумя или одним членом разложения, что соответствует ограничению разбавленными растворами.

Допущение о равенстве диэлектрической проницаемости раствора диэлектрической проницаемости растворителя также справедливо только для разбавленных растворов. Наконец, в теории не учитывается взаимодействие ионов с растворителем.

Все это приводит к тому, что теория оказывается применимой к очень разбавленным растворам и уравнение (15.65) является первым приближением, илипредельным закономтеории Дебая – Гюккеля. Попытки усовершенствования теории предпринимались как Дебаем и Гюккелем, так и другими исследователями. Вовтором приближенииавторы теории учли, что ионы имеют конечные размеры, и расстояние между ними не может быть меньше некоторой минимальной величины. Полученное во втором приближении выражение для коэффициентов активности имеет вид:

, (15.66)

где ,a– расстояние наибольшего сближения ионов. Эту величину можно рассматривать как средний эффективный диаметр ионов. Значениеaтеоретически не вычисляется, а подбирается эмпирически.

На практике часто используют также полуэмпирическое уравнение

, (15.67)

где C– эмпирическая постоянная. Это уравнение описывает зависимость коэффициентов активности от ионной силы в довольно широкой области концентраций.