5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ

Тема 5.1. Дифференцирование функции двух переменных

Определение 5.1 Переменная : называется функцией двух независимых переменных (аргументов) и , если каждой паре значений из множества соответствует одно определенное значение .

Функция двух переменных, обозначается так

и т.п.

Область называется областью определения (существования) функции . Аналогично определяются функции любого числа аргументов . Поэтому в дальнейшем будем, как правило, рассматривать, не нарушая общности, функции двух независимых переменных.

Определение 5.2 Частной производной от функции по независимой переменной, например , называется производная

,

вычисленная при постоянном значении другого аргумента -.

Поэтому частные производные находят по правилам дифференцирования функции одной переменной, считая остальные переменные константами. Можно использовать различные обозначения, частной производной:

.

Аналогично определяется частная производная по переменной .

Определение 5.3 Полным приращением функции в точке называется величина

,

где - приращения аргументов.

Определение 5.4 Главная, линейная относительно и , часть полного приращения функции называется полным дифференциалом . Так как при малых приращениях , то

.

Для дифференцирования сложных функций (т.е. функций, зависящих от промежуточных аргументов) используют следующие формулы:

Если а , , то

.

Если а , то

.

Если а , то

Функции нескольких переменных могут иметь частные производные и дифференциалы высших порядков.

Определение 5.5 Частными производными -го порядка от функции называются производные от ее частных производных -го порядка. Так, частные производные второго порядка обозначаются так:

;

.

Две последние частные производные называются смешанными и для непрерывных функций они совпадают. Дифференциалы высших порядков могут быть найдены по следующей символической формуле

.

В частности, для второго и третьего порядков получим такие зависимости:

.

Определение 5.6 Производной функции в точке в направлении вектора называется предел

,

где - направляющие косинусы вектора .

Определение 5.7 Градиентом функции в точке называется вектор, выходящий из указанной точки и имеющий своими координатами частные производные функции :

.

Градиент является направлением наибольшего роста функции в данной точке.

Существует зависимость

.

Тема 5.2. Исследование функций двух переменных

Для определения экстремальных точек функции проверяют выполнение двух условий существования экстремума.

Теорема 5.1 Необходимое условие: и , или обе частные производные не существуют. Тем самым определяются критические точки .

Теорема 5.2 Достаточное условие. Обозначим , , , .

Тогда будем иметь:

- если , то в точке существует экстремум, а именно: максимум при или минимум при ;

- если , то в точке экстремума нет;

- если , то требуется дополнительное исследование в этой точке.

Задача 5.1 Найти область определения, а также частные производные и дифференциал второго порядка функции .

Решение

Область определения данной функции ограничены условием или , т.е. представляет собой множество точек плоскости, лежащих вне единичного круга.

Далее последовательно находим

; ;

; ;

.

Задача 5.2 Найти:

а) если ;

б) и если ;

в) , если , , .

Решение

а)

б)

.

в)

.

Задача 5.3 Найти градиент к производную по направлению вектора функции в точке .

Решение

По определению

Предварительно найдем значение частных производных в точке и направляющие косинусы вектора: .

,

Задача 5.4 Определить размеры прямоугольного паралле­ле­пи­пе­да с диагональю , имеющего максимальный объем.

Решение

Пусть и - длины ребер параллелепипеда. Тогда его объем

.

Так как , то и .

Очевидно, что , , , .

Множество точек , удовлетворяющих этим требо­ва­ни­ям, можно изобразить так (рис.5.1):

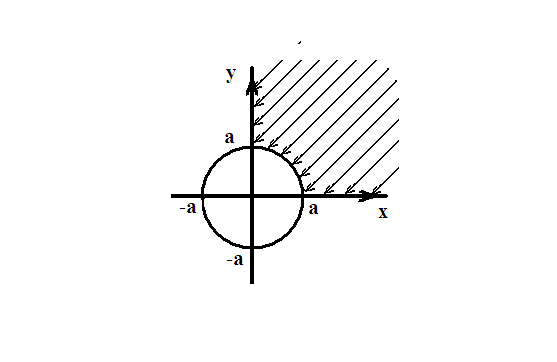
Рис. 5.1

Для нахождения точек экстремума приравняем к нулю частные производные функции :

Отсюда

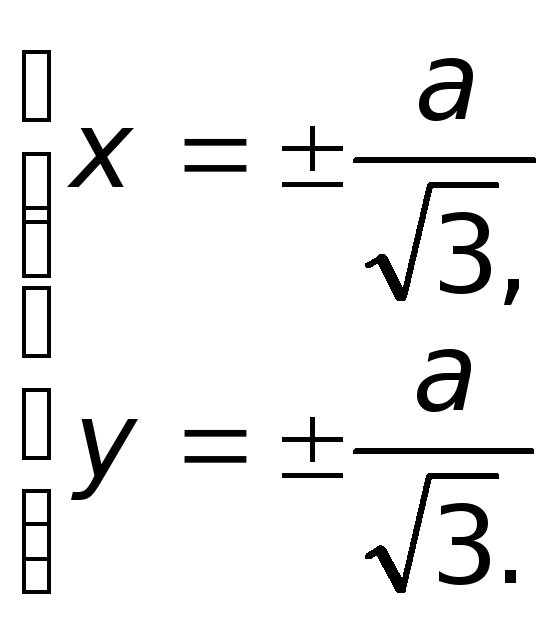
Итак, имеем 4 критические точки:

; ; ;

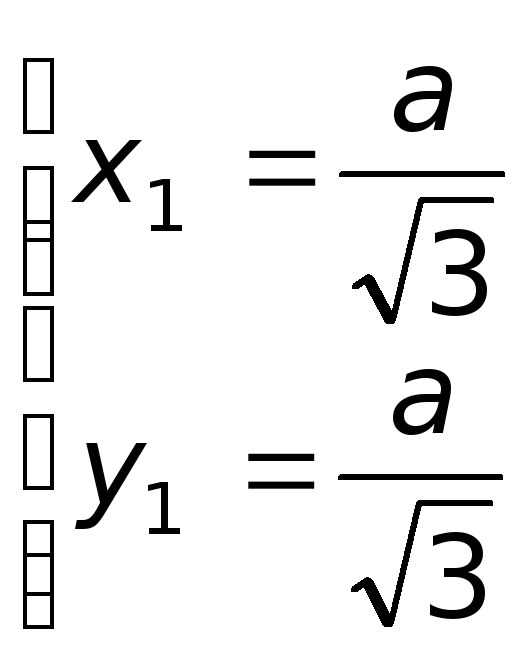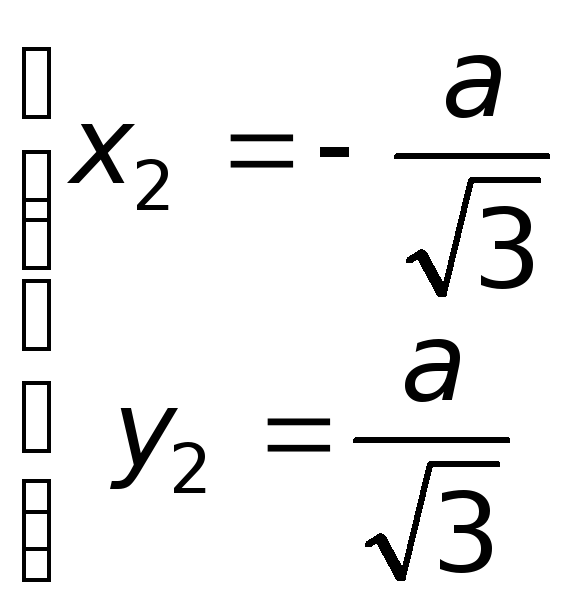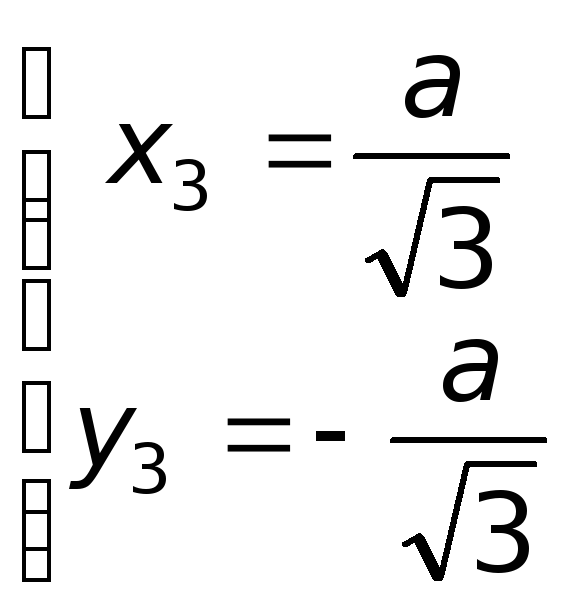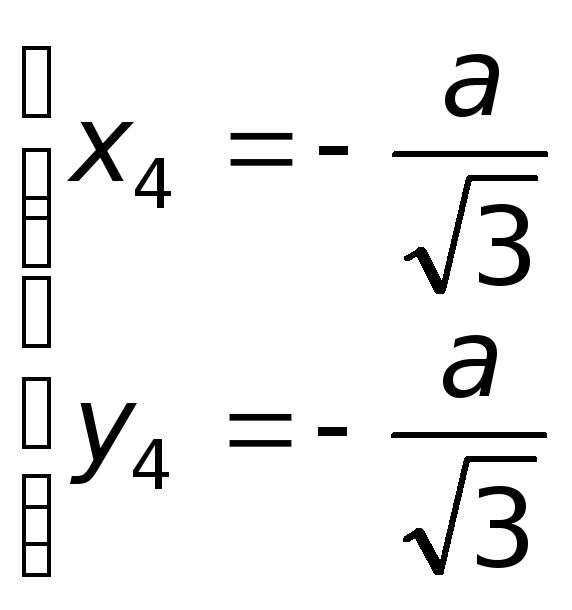
Условию задачи удовлетворяет только первая точка .

Проверим выполнение в этой точке достаточного условия существования экстремум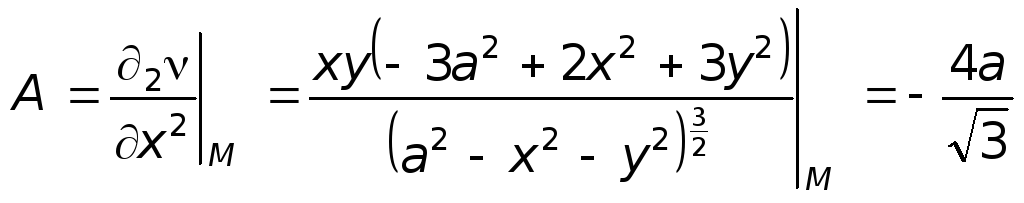а.

А=

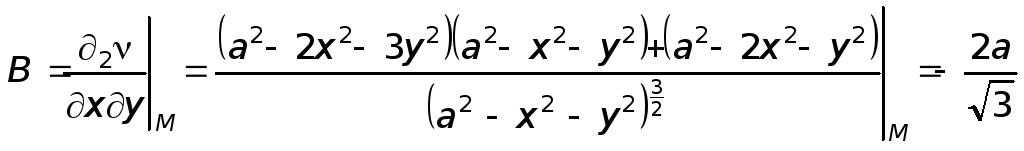
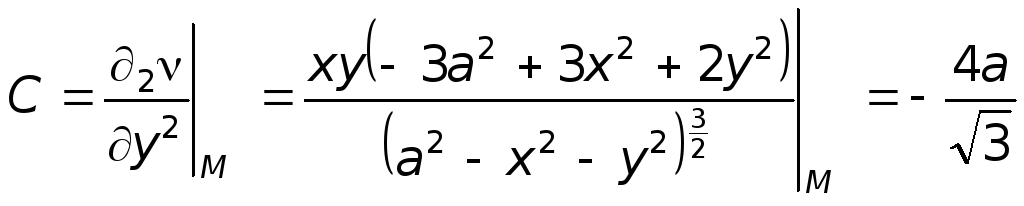
Следовательно, в точке М существует экстремум, а именно максимум .

Зная и , найдем :

Значит, .

Итак, изо всех прямоугольных параллелепипедов с фиксированной диагональю максимальный объем имеет куб с ребром, равным .

86