
- •4. Аеродинамічні сили та моменти
- •5. Опори руху
- •6. Привод, характеристика двигуна, передатні числа
- •6.2. Поршневий двигун внутрішнього згоряння
- •7. Споживання потужності
- •7.2. Максимальна швидкість на горизонтальній дорозі
- •10. Одномасова система
- •11. Збурення коливань, критерії оцінки, випадкові коливання
- •15. Рух по колу (спрощений підхід)
10. Одномасова система
10.1. Власні коливання, стабільність
Розглянемо одномасову систему з масою m, яка рухається в напрямі осі z (рис. 10.1). Випадок z = 0 відповідає статичному положенню рівноваги і означає, що статична деформація пружини під впливом ваги m∙g врахована.
|
|
Рис. 10.1. Одномасова система: а — система з масою m, жорсткістю пружини c і коефіцієнтом демпфування k, б — сили, що діють на систему (сила пружини Fп, сила демпфування Fд) |
Рівняння руху має вигляд
|
|
(10.1) |
де сила пружини
|
|
(10.2) |
і сила демпфування
|
|
(10.3) |
Ці сили пропорційні
до відносного переміщення
![]() чи відносної швидкості
чи відносної швидкості![]() ,
а також до коефіцієнтів:c
— жорсткості пружини і k
— сталої демпфера (рис. 10.2).
,
а також до коефіцієнтів:c
— жорсткості пружини і k
— сталої демпфера (рис. 10.2).
|
|
Рис. 10.2. Лінійні характеристики: а — пружини; б — демпфера |
Ця система є лінійною, бо, підставляючи рівняння (10.2) і (10.3) в рівняння (10.1), отримуємо лінійне диференціальне рівняння
|
|
(10.4) |
Залежну від часу
функцію h,
відповідно
![]() ,
що знаходиться в правій частині рівняння
і спонукає систему до коливань, будемо
називати функцією збурення.
,
що знаходиться в правій частині рівняння
і спонукає систему до коливань, будемо
називати функцією збурення.
Загальний розв’язок z рівняння (10.4) складається з загального розв’язку zо однорідного рівняння (права частина рівна нулю) і частинного розв’язку zч неоднорідного рівняння (права частина нерівна нулю)
|
|
(10.5) |
В цьому розділі займатимемося розв’язуванням однорідного рівняння
|
|
|
Поділивши на m і ввівши позначення (будуть означені пізніше)
|
|
(10.6) |
та
|
|
(10.7) |
отримуємо
|
|
(10.8) |
Розв’язок цього однорідного лінійного рівняння, відомий з математики, має вигляд
|
|
(10.9) |
Розв’язок і його
похідні
![]() і
і![]() підставляємо в рівняння (10.8)
підставляємо в рівняння (10.8)
|
|
(10.10) |
В цьому рівнянні
![]() не може
бути тотожно рівним нулю, бо рівняння
(10.9) не описувало би тоді жодних переміщень
z.
Тож маємо
не може
бути тотожно рівним нулю, бо рівняння
(10.9) не описувало би тоді жодних переміщень
z.
Тож маємо
|
|
(10.11) |
Це рівняння, зване характеристичним, має два розв’язки
|
|
(10.12) |
і тим самим для переміщень за рівнянням (10.9)
|
|
(10.13) |
Перебіг переміщень в часі характеризується обома значеннями λ. Можливі чотири різні випадки.
1.
Значення
![]() є дійсним, тож повинно бути σ2
> ν2.
До того ж σ є додатним, а λ2
— від’ємним. Натомість λ1
є тоді від’ємним, коли ν2
> 0, бо тільки тоді
є дійсним, тож повинно бути σ2
> ν2.
До того ж σ є додатним, а λ2
— від’ємним. Натомість λ1
є тоді від’ємним, коли ν2
> 0, бо тільки тоді
![]() .
.
В цьому випадку
обидві складові рівняння (10.13)
зменшуються
до нуля, коли t
прямує до нескінченості. Ця система, як
показує рис. 10.3а,
повертається до положення рівноваги
![]() .
Рух є стабільний.
.
Рух є стабільний.
|
Переміщення |
Монотонне
|
Осциляційне
|
|
зменшується стабільне
σ > 0, ν2 >0 |
|
|
|
збільшується нестабільне
σ < 0, ν2 > 0 чи σ < 0, ν2 <0 |
|
|
|
Рис.
10.3. Корені
| ||
2.
Натомість, коли ν2
є від’ємне, то
![]() і λ1
є додатним. Тоді
і λ1
є додатним. Тоді
![]() разом з часом прямує до нескінченості,
а
разом з часом прямує до нескінченості,
а![]() — до нуля. Система не повертається до
положення рівноваги, є нестабільною.
— до нуля. Система не повертається до
положення рівноваги, є нестабільною.
Нестабільні
перебіги отримаємо також при дійсних
значеннях
![]() ,
додатнім ν2,
але від’ємним σ. λ1
і λ2
тоді додатні, тож zо
прямує до нескінченості (10.3б).
,
додатнім ν2,
але від’ємним σ. λ1
і λ2
тоді додатні, тож zо
прямує до нескінченості (10.3б).
Якщо ж σ і ν2 від’ємні, отримаємо також нестабільний перебіг, бо λ1 є додатне.
3.
Якщо ν2
> σ2,
значення кореня не є дійсне, а уявне.
Позначимо
![]() ,
тож
,
тож
|
|
|
Комплексним спряженим кореням характеристичного рівняння відповідають комплексні спряжені амплітуди
|
|
|
Переміщення, відповідні рівнянню (10.13), набувають вигляду
|
|
|
а після перетворення
|
|
|
Скориставшись рівнянням Ейлера
|
|
|
отримуємо
|
|
(10.14) |
Це рівняння описує
коливання, представлені на рис. 10.3в
з круговою частотою
![]() ,
амплітуда яких для σ > 0 гасне за функцією
,
амплітуда яких для σ > 0 гасне за функцією![]() .
Рівняння (10.14) можна звести до вигляду
.
Рівняння (10.14) можна звести до вигляду
|
|
(10.15) |
де амплітуда
|
|
(10.16) |
а кут фазового зміщення
|
|
(10.17) |
(Виведення буде представлене в підрозділі 10.2).
Такі власні гашені коливання характеризуються величиною σ, вирішальною щодо швидкості згасання коливань і названою коефіцієнтом демпфування
|
|
|
а також круговою частотою власних гашених коливань
|
|
(10.18) |
Якщо σ = 0, коливання
не згасають і є негашені. Тоді
![]() є означена як кругова частота власних
негашених коливань
є означена як кругова частота власних
негашених коливань
|
|
(10.18б) |
Введемо наступну, часто подальше вживану, величину — безвимірний коефіцієнт демпфування
|
|
(10.19) |
Підставляючи цю величину до рівняння (10.18), отримуємо залежність
|
|
(10.20) |
графічним
відображенням якої є коло (рис. 10.4). Якщо
0 < D
< 1, то
маємо справу з гашеними коливаннями,
натомість для D
> 1 отримуємо
гашений
аперіодичний рух (рис. 10.3а).
У випадку коливань автомобілів D
набуває значення порядку 0,25. З рис. 10.4
видно, що тоді
![]() .
.
4.
Якщо значення кореня в рівнянні (10.12) є
уявним, а σ < 0, отримуємо (як у випадку
3) коливання частотою
![]() ,
амплітуда яких не зменшується, а росте.
Така система називається нестабільною
(рис. 10.3г).
,
амплітуда яких не зменшується, а росте.
Така система називається нестабільною
(рис. 10.3г).
|
|
|
|---|
На рис. 10.3 представлені, відповідно впорядковані, монотонні і осциляційні перебіги, стабільні і нестабільні, а також відповідні критерії оцінки. На їх підставі можна остаточно ствердити, що система може бути стабільною тільки тоді, коли всі коефіцієнти характеристичного рівняння як σ, так і ν2 є додатні.
Для коливних рухів, якими будемо займатись, а також для прикладу одномасової системи з рис. 10.1 виступатимуть завжди стійкі перебіги. Найчастіше будемо стикатись з гашеними коливаннями, для яких, як вже згадувалось, D ≈ 0,25. При обговоренні стійкості руху автомобіля (розділ 18) ознайомимось з нестабільними перебігами.
10.2. Вимушені коливання
Перейдемо тепер до неоднорідного рівняння (10.4) і знайдемо його частинний розв’язок за рівнянням (10.5). Цей розв’язок має велике значення у випадку стабільних систем, до яких належать підвіски автомобілів. З рівнянь (10.5) і(10.15) випливає, що через певний час переміщення системи залежать тільки від zч, бо zо прямує до нуля.
Найчастіше як збурювальну застосовують гармонічну функцію
|
|
(10.21) |
При знаходженні розв’язку зручніше записати збурювальну функцію (10.21) в комплексному вигляді, тож з’ясуємо основні засади цього перетворення.
Вектор довжиною
b
обертається з кутовою швидкістю ω в
напрямі, прийнятому в математиці за
додатній (рис. 10.5а).
Проекція руху вектора на пряму дає образ
гармонічного руху. Якщо на рисунку та
пряма є вісь ординат, а відлік часу
ведеться від осі абсцис, то отримуємо
графік функції
![]() (рис. 10.5а).
Натомість, коли ця пряма є віссю абсцис
отримуємо графік функції
(рис. 10.5а).
Натомість, коли ця пряма є віссю абсцис
отримуємо графік функції
![]() ,
а при нахилі прямої до осі абсцис під
кутом ψ — функцію
,
а при нахилі прямої до осі абсцис під
кутом ψ — функцію![]() .
.
|
|
|
Рис. 10.5. Гармонічний перебіг у векторній формі (а) і як функція часу (б) |
Положення вектора на площині рис. 10.5а і його поворот можна записати за допомогою його координат. Для комплексних чисел застосовується система координат, в якій додатній напрям дійсної осі (Re) позначений через + 1, а додатній напрям уявної осі (Im) + i. В такий спосіб вектор на рис. 10.6 можемо описати за допомогою комплексних чисел, які для відміни будуть позначатись товстим друком
|
|
(10.22) |
|
|
Рис. 10.6. Представлення вектора b з дійсною частиною bre і уявною частиною bim на комплексній площині |
Довжина вектора
![]() і кут фазового зміщення ψ становлять:
і кут фазового зміщення ψ становлять:
|
|
|
|
|
|
Підставимо в рівняння (10.22) вирази
|
|
|
і на підставі рівняння Ейлера отримаємо
|
|
(10.23) |
Якщо кут ψ є змінними
в часі як, наприклад, на рис. 10.5, де
![]() ,
то обертовий вектор можна описати
рівнянням
,
то обертовий вектор можна описати
рівнянням
|
|
|
Це є частиний
випадок, бо при
![]() вектор переходить через вісь абсцис,
тож в загальному випадку векторb,
якого кут
вектор переходить через вісь абсцис,
тож в загальному випадку векторb,
якого кут
![]() складається зі сталої частини ψ і змінної
частини ω∙t
можна записати
складається зі сталої частини ψ і змінної
частини ω∙t
можна записати
|
|
|
і за рівнянням (10.23)
|
|
(10.24) |
![]() називається
комплексною амплітудою, яка описує
величину і положення вектора
називається
комплексною амплітудою, яка описує
величину і положення вектора
![]() при
при![]() .
.
Збурювальну функцію
![]() з рівняння(10.21)
подається
як проекція
вектора на уявну вісь за рівнянням
(10.24)
з рівняння(10.21)
подається
як проекція
вектора на уявну вісь за рівнянням
(10.24)
|
|
|
Аби спростити запис, вважатимемо відтепер, що проективною віссю є уявна вісь, і будемо писати тільки
|
|
(10.25) |
Оскільки для лінійної системи з гармонічним збуренням отримані переміщення і сили будуть теж гармонічними, розв’язок неоднорідного рівняння можна подати у вигляді
|
|
(10.26) |
Підставляючи (10.25) і (10.26) до рівняння (10.4), отримуємо
|
|
(10.27) |
тож є можливість визначити a для даного b. Це рівняння з комплексними величинами можна відобразити на комплексній площині
|
|
Рис. 10.7. Векторний графік як відображення вимушених коливань одномасової системи за рівнянням (10.27) |
Вважаючи довжину
вектора a
відомою, відкладемо її та її помножену
на с
на дійсній осі. З кінця отриманого
вектора перпендикулярно відкладаємо
вектор k∙ω∙a.
Тоді знову перпендикулярно, у від’ємному
напрямі дійсної осі, відкладемо вектор
m∙ω2∙a.
Рівнодійна цих трьох векторів повинна
бути за рівнянням (10.27) рівна
![]() .
Оскільки
.
Оскільки![]() та
та ![]() взаємно перпендикулярні, легко визначити
взаємно перпендикулярні, легко визначити
![]() ,
а потім
,
а потім ![]() .
Видно, що на комплексній площині вектори
a
і b
мають різні довжини та між ними виникає
кут фазового зміщення ψ.
.
Видно, що на комплексній площині вектори
a
і b
мають різні довжини та між ними виникає
кут фазового зміщення ψ.
На рис. 10.8 показана залежність довжин векторів a і b для різних значень ω. З цього векторного поля можна визначити |b| та ψ. Залежність відношення
|
|
Рис. 10.8. Векторний графік за рівнянням (10.27) для різних частот збурення |
амплітуд |a/b| = a/b та кута фазового зміщення ψ від частоти збурення ω представлено на графіку рис. 10.9. Відношення a/b часто називається коефіцієнтом підсилення, а залежність a/b від ω — амплітудно-частотною характеристикою.
|
|
|
Рис. 10.9. Резонансна характеристика: коефіцієнт підсилення a/b і кут фазового зміщення ψ в функції відношення частоти збурення ω до частоти власних коливань ν для одномасової системи з безвимірним коефіцієнтом демпфування D = 0,2 |
Для ω = 0 отримуємо a = b і ψ = 0. Для ω, близьких частоті власних коливань ω ≈ ν, в зоні резонансу a досягає максимуму, а при подальшому зростанні ω — прямує до нуля.
Вираз для коефіцієнта підсилення в комплексному вигляді можна
отримати з рівняння (10.27)
|
|
|
З врахуванням
![]() ,
де частота власних коливань за рівнянням
(10.7)
,
де частота власних коливань за рівнянням
(10.7)![]() , а безвимірний коефіцієнт демпфування
за рівнянням (10.19)
, а безвимірний коефіцієнт демпфування
за рівнянням (10.19)![]() ,
отримуємо
,
отримуємо
|
|
(10.28) |
Тож коефіцієнт підсилення є залежним від двох безвимірних величин: коефіцієнта демпфування D і відношення частот η. Застосовуючи загальний запис
|
|
|
отримуємо коефіцієнт підсилення
|
|
(10.29) |
і фазового зміщення
|
|
(10.30) |



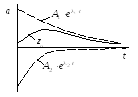



 Рис.
10.4. Залежність відношення кругової
частоти власних гашених коливань νg
від безвимірного коефіцієнта демпфування
Рис.
10.4. Залежність відношення кругової
частоти власних гашених коливань νg
від безвимірного коефіцієнта демпфування



