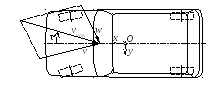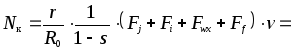- •4. Аеродинамічні сили та моменти
- •5. Опори руху
- •6. Привод, характеристика двигуна, передатні числа
- •6.2. Поршневий двигун внутрішнього згоряння
- •7. Споживання потужності
- •7.2. Максимальна швидкість на горизонтальній дорозі
- •10. Одномасова система
- •11. Збурення коливань, критерії оцінки, випадкові коливання
- •15. Рух по колу (спрощений підхід)
Частина II. Привод і гальмування
В цій частині розглянуті сили опору руху, а також проблеми прямолінійного руху автомобіля: максимальна швидкість, прискорення і сповільнення, здатність долати підйоми, необхідна потужність та потреба в перетворювачі, витрата палива, розподіл гальмівних сил.
II.1. Рівняння руху
Дослідження окреслених задач проводитиметься на прикладі двовісного автомобіля рис. II.1.
|
| |
|
| |
|
|
Рис. II.1.Сили, що діють на автомобіль в процесі руху: а — положення центрів мас; б — сили і моменти, що діють на кузов автомобіля; в — сили і моменти, що діють на осі та колеса; г — сили, що діють на дорогу |
Автомобіль, розділений на основні частини — кузов і осі коліс, для яких укладатимуться рівняння руху. Розглядатиметься плоска модель, що передбачає однаковість тягових чи гальмівних сил на лівому та правому колесах, тож для кожної частини існують три рівняння руху:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система координат x−z зв’язана з автомобілем; x вказує напрям руху, а z перпендикулярна до дороги. Якщо знехтувати деформацією підвіски і шин, то рівняння руху основних частин автомобіля матимуть вигляд:
а) кузова автомобіля вагою G3, масою m3 і координатами центру мас l1, l2,.h
|
|
(II.1) |
|
|
(II.2) |
|
|
(II.3) |
б) коліс передньої осі вагою G1, масою m1, моментом інерції I1 і врахуванням опору кочення зміщенням e1
|
|
(II.4) |
|
|
(II.5) |
|
|
(II.6) |
в) коліс задньої осі вагою G2, масою m2, моментом інерції I2 і врахуванням опору кочення зміщенням e2
|
|
(II.7) |
|
|
(II.8) |
|
|
(II.9) |
![]() є силою опору
повітря.
є силою опору
повітря.
Додаючи рівняння (II.1), (II.4) і (II.7), знаходимо
|
|
|
Враховуючи, що:
|
|
|
|
|
|
|
|
|
остаточно отримуємо
|
|
(II.10) |
Тож окружні сили
виникають за умови існування сили
інерції
![]() ,
опору підйому
,
опору підйому![]() і опору повітря
і опору повітря![]() .
.
Для розгону автомобіля і подолання опорів руху необхідно прикласти обертові моменти, що визначаються з рівнянь (II.6) і (II.9)
|
|
(II.11) |
Використовуючи рівняння (II.10) і позначаючи суму опорів кочення всіх коліс передньої та задньої осей як
|
|
(II.12) |
маємо
|
|
|
Кутові прискорення можна виразити через прискорення поступального руху
|
|
|
тож сума обертових моментів, поділена на відстань вісь колеса — дорога r, остаточно має вигляд
|
|
(II.13) |
Рівняння (II.13)
відрізняється від рівняння (II.10) тим, що
в ньому появились: моменти інерції I1,
I2
і опір кочення Ff,
які у рівнянні (II.10) містяться в сумі
![]() у не явному вигляді.
у не явному вигляді.
4. Аеродинамічні сили та моменти
4.1. Визначення аеродинамічного опору
Опір повітря спричинений: тертям та вихроутворенням в прилеглих до кузова шарах повітря, стиском повітря рухомим автомобілем, розрідженням за автомобілем. На рис. 4.1а показане обтікання повітря навколо автомобіля і позначена сила опору повітря Fwx . Величина цієї сили визначається рівнодійною
|
|
Рис. 4.1. Схеми: а — обтікання повітря навколо автомобіля ; б — дії сил напору (суцільні стрілки) і сил тертя (пунктирні стрілки) |
нормальних тисків
і питомих сил тертя (також з розмірністю
тиску), дотичних до зовнішньої поверхні
кузова, що омивається повітрям. В
інтервалі вживаних швидкостей потік є
турбулентним і сила опору пропорційна
—
![]() — густині повітря ρ і сумарній швидкості
напору
— густині повітря ρ і сумарній швидкості
напору![]() .
Стала пропорційності — це добуток двох
складових: коефіцієнта опоруcx
(характеризує обтічність автомобіля)
та лобової площі A
(найбільша площа поперечного перерізу
автомобіля). Отже, сила опору повітря
визначається як
.
Стала пропорційності — це добуток двох
складових: коефіцієнта опоруcx
(характеризує обтічність автомобіля)
та лобової площі A
(найбільша площа поперечного перерізу
автомобіля). Отже, сила опору повітря
визначається як
|
|
(4.1) |
4.2. Швидкість і напрям напору, густина повітря
Сумарна швидкість напору vсум складається з від’ємної швидкості руху v, з якою автомобіль рухається в середовищі нерухомого повітря, і швидкості вітру w (рис. 4.2). На рисунку розглянутий загальний випадок, коли швидкість руху не співпадає з поздовжньою віссю автомобіля, наприклад рух на повороті.
|
|
Рис. 4.2. Схема знаходження сумарної швидкості напору vсум геометричним додаванням швидкості руху v і швидкості вітру w |
У векторній формі маємо
|
|
(4.2) |
Кут між сумарною швидкістю напору і поздовжньою віссю автомобіля називається кутом напору τ. Як буде видно з подальших розділів, на величину цього кута головне впливають: бічна сила напору, сила опору повітря і аеродинамічні моменти відносно вертикальної та поздовжньої осей.
Напрям швидкості вітру відносно поздовжньої осі автомобіля залежить від напряму вітру і перебігу дороги, по якій рухається автомобіль, тобто є випадковим. Розглядатимуться два особливі випадки:
1.Вітер дує тільки вздовж поздовжньої осі автомобіля спереду чи ззаду, тож рівняння (4.15) спрощується до вигляду
|
|
(4.3) |
|
|
(4.4) |
В цьому випадку за сталої швидкості руху потужність приводу є зменшувана чи збільшувана, відповідно — швидкість руху за сталої потужності приводу є зменшувана чи збільшувана.
2. Вітер дує перпендикулярно до поздовжньої осі автомобіля, тож отримуємо
|
|
(4.5) |
|
|
(4.6) |
5. Опори руху
Після розгляду аеродинамічної сили додамо опори, сума яких повинна бути подолана приводним моментом, а величина яких визначає потужність застосованого двигуна.
5.1. Опір руху на колесах автомобіля
Опір кочення становить
|
|
(5.1) |
і є сумою опорів кочення всіх коліс передньої і задньої осей. Замість e1/r і e2/r підставимо коефіцієнти опору кочення коліс передньої (fк)1 і задньої (fк)2 осей
|
|
(5.2) |
Останній вираз може відображати опір кочення окремих коліс 11, 12, 21, …
|
|
(5.3) |
Зазвичай коефіцієнти опору кочення всіх коліс приймаються однаковими, а сума вертикальних реакцій дорівнює вазі автомобіля G·cosν
|
|
(5.4) |
тож можна записати
|
|
(5.5) |
Це рівняння часто спрощується шляхом застосування допустимим при нормальних ухилах доріг cosν = 1
|
|
(5.6) |
5.2. Опір повітря
З підр. 4.1 відомо, що опір повітря становить
|
|
(5.7) |
Коефіцієнт опору повітря cx розглянутий в підр. 4.3, а значення cx, A і добутку cx·A подані в таблиці 4.2. Лобова площа може бути визначена через ширину b і висоту h автомобіля. Для легкових автомобілів A завжди міститься в проміжку 0,7·b·h…0,85·b·h, тож середньо
|
|
(5.8) |
Рівняння (5.17) можна легко запам’ятати, якщо підставити середнє значення ρ з підр. 4.2
|
|
|
а швидкість v виразити в км/год
|
|
(5.7а) |
5.3. Опір підйому
Опір підйому означає
|
|
(5.9) |
Для зручності sinν можна замінити на tgν ідентичний ухилу i, що дає похибку до 5% аж до ν = 17° (відповідає ухилу i = 0,3). Таке спрощення допустиме при обчисленні опору підйому на твердих дорогах.
|
|
(5.10) |
а
|
|
(5.11) |
Наприклад, при ухилі 8% (ухил i зазвичай подається в %), тобто i = 0,08 дорога довжиною 100 м, відлічена горизонтально, піднімається на 8 м. Опір підйому Fi становить 8% ваги автомобіля G.
5.4. Опір інерції
За рівнянням (II.13) обертовий момент, потрібний для розгону автомобіля і віднесений до відстані r між віссю колеса і дорогою, становить
|
|
(5.12) |
Цей вираз називається
опором інерції Fj
і містить маси:
![]() — в поступальному русі та
— в поступальному русі та![]() — в обертальному. На відміну від загальної
маси
— в обертальному. На відміну від загальної
маси![]() оцінити вплив обертових мас важко. До
моментів інерціїI1
та I2
належать не тільки моменти інерції
коліс Iк,
гальмівних дисків, півосей, що обертаються
з кутовими швидкостями відповідно
оцінити вплив обертових мас важко. До
моментів інерціїI1
та I2
належать не тільки моменти інерції
коліс Iк,
гальмівних дисків, півосей, що обертаються
з кутовими швидкостями відповідно
![]() ,
,![]() чи загалом
чи загалом![]() ,
але й моменти інерції елементів механізмів
приводуIп
і двигуна Iд,
що обертаються з кутовими швидкостями
,
але й моменти інерції елементів механізмів
приводуIп
і двигуна Iд,
що обертаються з кутовими швидкостями
![]() і
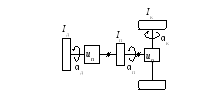
і![]() (рис. 5.1). Ці кутові швидкості зв’язані
через передатні відношення головної
передачіu0
та коробки передач uп:
(рис. 5.1). Ці кутові швидкості зв’язані
через передатні відношення головної
передачіu0
та коробки передач uп:
|
|
(5.13) |
|
|
(5.14) |
|
|
Рис. 5.1. Обертові маси, що враховуються при розрахунку сили опору інерції |
Отже, не можна
враховувати тільки моменти інерції
коліс як в підрозділі II.1, лише суму всіх
учасників сповільнення
![]() .
.
Зведення всіх
моментів інерції до колеса з кутовою
швидкістю
![]() за принципом збереження енергії
за принципом збереження енергії
|
|
|
дає
|
|
|
і відповідно
|
|
|
Звідси сума всіх учасників сповільнення дорівнює
|
|
|
що заміняє вирази:
для передньої осі
![]() та задньої
та задньої![]() .Опускаючи
індекси 1 і 2, отримуємо
.Опускаючи
індекси 1 і 2, отримуємо
|
|
|
тож загалом момент інерції становить
|
|
(5.15) |
Повертаючись до рівняння (5.12), наприклад, для приводу на задню вісь
|
|
(5.16) |
|
|
(5.17) |
У випадку приводу на передню вісь треба в обох рівняннях поміняти індекси 1 і 2. У випадку приводу на всі колеса належить сумувати моменти інерції елементів механізмів приводу передніх та задніх коліс.
Опір інерції Fj з рівняння (5.12) зазвичай виражається залежністю
|
|
(5.18) |
в якій коефіцієнт λ враховує вплив прискорення обертових мас. Цей коефіцієнт визначається з рівнянь (5.12) і (5.18)
|
|
(5.19) |
Якщо знехтувати проковзуванням та замінити R1 і R2 на динамічні радіуси шин R1,0 і R2,0, відповідно за однакових шин R0, то коефіцієнт λ стає незалежним від величини окружних сил і становить
|
|
(5.19а) |
Інколи приймається Rо ≈ r, тож
|
|
(5.19б) |
Відповідно при
![]()
|
|
(5.19в) |
5.5. Сумарний опір, тягова сила, потужність на відних колесах
За рівнянням (II.13) сума приводних моментів, поділена на відстань r осі колеса до дороги становить
|
|
|
В попередніх підрозділах розглянуті опори, що входять до правої частини цього рівняння, і впроваджені деякі зміни:
|
опору інерції |
|
|
опору підйому |
|
|
опору повітря |
|
|
опору кочення коліс |
|
Якщо позначимо через Tк суму моментів
|
|
(5.20) |
які діють на колеса, то
|
|
(5.21) |
Підставляючи отримані залежності в рівняння (5.21), зведемо його до вигляду
|
|
(5.22) |
За рівнянням (5.22) загальний опір має дві складові: група опорів майже незалежну від швидкості руху і опір повітря, що зростає з квадратом швидкості (рис. 5.2). Слово „майже” стосується опору кочення коліс. Опір кочення росте при більших швидкостях і особливо під час руху по нерівній дорозі.
Загалом прийнято записувати
|
|
(5.23) |
Множник b відноситься не тільки до опору повітря, а і до тої частини опору кочення, яка росте з квадратом швидкості. Якщо множник b визначався би під час тягових випробувань як опір повітря, то містив би теж частину опору кочення, залежну від швидкості руху заміру.
|
|
Рис. 5.2. Залежність тягової сили для подолання опорів руху від швидкості руху (швидкість вітру w = 0) |
Інколи вводиться ще один лінійний член, що теж враховує опір кочення
|
|
|
Будемо вживати
рівняння (5.33) і, при потребі, згадувати,
що
![]() не є незалежне від швидкості.
не є незалежне від швидкості.
Якщо однак вважати
![]() сталою величиною, то обидва члени
рівняння (5.33) відрізняються тим, що
незалежна від швидкості частина є
пропорційна до ваги, тоді як опір повітря
не є залежний від ваги.
сталою величиною, то обидва члени
рівняння (5.33) відрізняються тим, що
незалежна від швидкості частина є
пропорційна до ваги, тоді як опір повітря
не є залежний від ваги.
Вираз
![]() має розмірність сили і тому здебільшого
трактується як тягова силаFк
має розмірність сили і тому здебільшого
трактується як тягова силаFк
|
|
(5.24) |
Це зрештою спрощує запис, але важливо завжди пам’ятати, що Fк не є сумою окружних сил між колесом і дорогою, а лиш часткою від ділення моменту Tк на r. Це зауваження стає більш помітним, якщо до рівняння (II.13) підставити рівняння (II.10)
|
|
(5.25) |
Необхідна потужність на колесах є загалом сума всіх моментів помножена на кутову швидкість, тобто для двовісного автомобіля
|
|
(5.26) |
Виразимо кутові
швидкості
![]() і
і![]() через швидкість поступального руху
через швидкість поступального руху![]() та врахуємо проковзування коліс [1]
та врахуємо проковзування коліс [1]
|
|
(5.27) |
Тоді потужність
|
|
(5.28) |
У випадку приводу на одну вісь рівняння спрощується.
З рівняння (5.26) і врахування суми (5.20) отримаємо
|
|
(5.29) |
Оскільки, за рівнянням (5.27)
|
|
(5.30) |
то при введенні
до рівняння (5.29)
![]() і заміні
і заміні![]() наFк
буде
наFк
буде
|
|
(5.31) |
R
містить в собі проковзування
![]() ,
тож після підстановки отримаємо
,
тож після підстановки отримаємо
|
|
(5.32) |
і відповідно при виокремленні опорів
|
|
|
|
|
(5.33) |
Зазвичай
проковзуванням нехтують і приймають
![]() .
Отримуємо тоді просте означення приводної
потужності на колесах
.
Отримуємо тоді просте означення приводної
потужності на колесах
|
|
(5.33а) |
а у випадку безвітряної погоди
|
|
(5.33б) |
З графіка потужності
(рис. 5.3) видно, що потужність опору
кочення коліс
![]() ,
потужність опору підйому
,
потужність опору підйому![]() і потужність опору інерції
і потужність опору інерції![]() ростуть пропорційно до швидкостіv,
натомість потужність опору повітря
ростуть пропорційно до швидкостіv,
натомість потужність опору повітря
![]() — до третього степеня швидкостіv3.
— до третього степеня швидкостіv3.
|
|
Рис. 5.3. Перебіг зміни значень окремих складових приводної потужності на колесах в залежності від швидкості руху |