
Navch._posibnuk_Ivaschyk
.pdf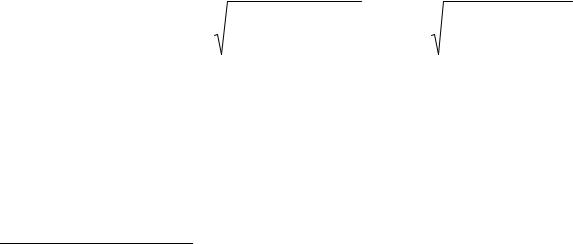
11.6. Систематичний і несистематичний ризик
У фінансовій теорії популярним є розподіл ризиків на два типи: систематичний і несистематичний.
Систематичний ризик β визначає рівень коливань або відхилень у результатах діяльності галузі щодо результатів діяльності ринку або всієї економіки. Він є частиною загального ризику, який залежить від загального стану економіки країни. Цей ризик впливає на всіх учасників господарського процесу й зумовлений динамікою інвестицій, оборотом зовнішньої торгівлі, змінами в законодавстві та ін. Систематичний ризик є одним з основних показників, що використовуються під час аналізу фінансових ризиків. Він знаходиться за формулою:
|
|
VR R |
|
σR |
|
|
||
β |
= |
|
i |
= ρR R |
i |
, |
(11.19) |
|
|
σR2 |
|
||||||
де R – випадкова величина, |
|
|
i |
σR |
|
|
||
що характеризує всю економіку; Ri |
– |
|||||||
випадкова величина, що характеризує і-у галузь; VR R |
– коефіцієнт |
|||||||
|
|
|
|
|
|
i |
|
|
коваріації між Ri та R; σR – середньоквадратичне відхилення R; σR |
– |
|||||||
|
|
|
|
|
|
|
i |
|
середньоквадратичне відхилення Ri ; ρRiR – коефіцієнт кореляції між
Ri та R.
Обчислення вищенаведених числових характеристик проводяться за такими формулами:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VRi R |
|
|
|
|
|
∑R R |
|
|
|
|
|
|
|
∑R |
|
||||
V |
|
= |
n |
( |
|
|
− |
|
|
|
)1, |
ρ |
|
= |
|
, |
|
= |
j=1 |
ij |
|
|
j |
, |
|
|
|
= |
j =1 |
ij |
, |
|||||||||||
|
R R |
R |
R |
|
|
R R |
|
|
|
|
R |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
RiR |
|
|
n −1 |
|
|
i |
|
|
i |
|
|
|
Ri R |
|
|
σRi σR |
i |
|
|
|
n |
|
|
|
|
|
|
i |
|
n |
|
|
|||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Rj |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
R = |
|
, σ |
R |
= |
|
∑ |
(R − R )2 / n , σ |
R |
= |
∑(R |
j |
− R)2 |
/ n . |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
ij |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Систематичний ризик ще називають ринковим ризиком або недиверсифікованим. Вимірюють його величину, як бачимо, коефіцієнтом чутливості β . За допомогою цього показника можна
порівнювати діяльність підприємств і галузі, ефективність акцій з ефективністю всього ринку цінних паперів і т.д. Його інтерпретують так: коефіцієнт β вказує, на скільки відсотків наближено зросте
1 Коефіцієнт n/(n-1) використовується у випадку n<15, при n≥15 коефіцієнт дорівнює одиниці
341
(знизиться) норма прибутку акції, якщо норма прибутку ринку зросте (знизиться) на 1%.
Існують твердження:
•β = 1, то це означає, що досліджувана галузь має коливання результатів, які дорівнюють ринковому;
•β < 1 – коливання результатів менші за ринкові;
•β > 1 – коливання результатів більші за ринкові.
Чим більший показник β, тим вищим є ризик пов’язаний із зазначеною галуззю.
Значення коефіцієнта β регулярно публікуються у фінансовій періодиці країн з розвинутою ринковою економікою. Обчислення його не є складним. Проте дослідження економістів дають статистичні свідчення того, що β нестійкий, він не відображає обчислені на підставі інформації минулого періоду прогнози інвесторів щодо ризику у майбутньому. І тим більше, β обчислені на минулих даних, не можуть відбити ризик, який відчували інвестори в пізнішому періоді.
Крім цієї проблеми, дослідження показують, що є ще й інша проблема: з часом β наближається до одиниці. Наприклад, якщо акція в період 1995-2003 р.р. мала обчислене значення β=0,7, то в 20032008 р.р. воно буде вище й знаходитиметься в діапазоні 0,7-1,0 і, навпаки, якщо β за період 1995-2003 р.р. дорівнював 1,6, то в період 2003-2008 р.р. ймовірно, що β буде знаходитися в діапазоні 1,0-1,6. За цієї причиною економісти майбутні значення β обчислюють як середньозважені значення β за минулий період. Наприклад,
βмайб = 0,6 βпопередній + 0,4 1,0.
Ваги 60 % і 40 % кожна фірма вибирає зі своїх міркувань і, як правило, не розкриває методику їхнього підбору, крім того, змінює їх з часом.
На розвинених фондових ринках, де регулярно розраховують значення відповідних ринкових (фондових) індексів, існує чітка класифікація акцій за ступенем ризику відповідно до граничних значень коефіцієнта чутливості β (табл. 11.6).
342

|
|
Таблиця 11.6 |
|
|
Класифікація акцій за ступенем ризику |
||
Значення |
Економічна суть |
Ступінь ризику |
|
|
Рідкісний випадок, дохідність акції та |
|
|
β < 0 |
ринкового портфеля пов’язані оберненою |
|
|
|
залежністю |
|
|
|
Дохідність акції не залежить від змін, що |
Ризику майже |
|
β = 0 |
відбуваються на ринку. Тобто це без |
||
немає |
|||
|
ризикові цінні папери |
||
|
|
||
|
Дохідність акції досить помірковано |
Ризик нижчий за |
|
0 < β <1 |
реагує на зміни на ринку. Такі акції |
||
середньоринковий |
|||
|
називають захисними |
||
|
|
||
|
Дохідність акції змінюється такою самою |
Ризик на рівні |
|
β =1 |
мірою, як середньо ринкова дохідність. Та- |
||
середньоринкового |
|||
|
кий коефіцієнт має сам ринковий портфель |
||
|
Дохідність акції значною мірою залежить |
Ризик вищий за |
|
β >1 |
від змін, що відбуваються на ринку. Такі |
||
середньоринковий |
|||
|
акції називають агресивними |
||
|
|
||
Приклад 11.7. У табл. 11.7 вказані дані ефективності роботи металургійного комбінату й ефективності роботи металургійної промисловості за останні 10 періодів.
Таблиця 11.7
Ефективність роботи |
20 |
15 |
12 |
10 |
12 |
6 |
-2 |
-4 |
3 |
5 |
металургійного комбінату (Х) |
||||||||||
Ефективність роботи металур- |
30 |
20 |
10 |
8 |
9 |
-2 |
-5 |
-2 |
-2 |
3 |
гійної промисловості (Y) |
|
|
|
|
|
|
|
|
|
|
Обчислити коефіцієнт чутливості β і зробити висновки щодо стабільності роботи металургійного комбінату порівняно з усією металургійною промисловістю.
♦Розв’язування.
x = 7,7, y = 6,9, y2 = 159,1, σy2 = 111,49,
xy = (20 30 +15 20 +12 10 +10 8 +12 9 −6 2 + 2 5 + 4 2 −3 2 +5 3) = 10
=122,3,
Vxy = nn−1(xy − x y) =109 (122,3 −7,7 6,9) =76,86. Отже, β = 76,86/111,49 = 0,689 < 1.
343

Оскільки β < 1, то металургійний комбінат працює стабільніше, ніж вся металургійна промисловість. ♦
Приклад 11.8. Відомі статистичні дані за 10 послідовних періодів часу про щотижневу дохідність акцій компанії N (YN) та щотижневу дохідність ринкового портфеля, що складений на основі фондового індексу М (YМ) (табл. 11.8). Необхідно підрахувати β акцій компанії N.
Таблиця 11.8
YМ |
4 |
0,5 |
–1 |
0,5 |
2 |
3,5 |
–0,6 |
0,5 |
–0,5 |
–2 |
YN |
2 |
3 |
1,5 |
6 |
4 |
3 |
2,5 |
–2 |
–3 |
–4 |
♦Розв’язування.
Обчислимо β за формулою (11.19). Щоб уникнути громіздких обчислень коваріації і дисперсії вручну, використаємо відповідні стандартні статистичні функції пакету MS Excel – КОВАР та ДИСП:
cov(YM ,YN ) = 2,753, σM2 = 3,761, β = 23,,761753 0,732.
Оскільки 0 < β <1, то вкладення коштів у такі акції менш
ризикові, ніж в середньому на ринку. ♦ Крім систематичного ризику, розрізняють і ризик
несистематичний. Це обставини, щодо кожного підприємства зокрема, є характерними лише для нього і не залежать від загального економічного клімату. Вони змушують змінювати прибутки підприємства за певною акцією незалежно від зміни інших акцій на ринку. Такі події характеризуються терміном шок.
Наприклад, підприємство випускало обладнання для металургійного комбінату. У зв’язку із закриттям металургійного комбінату зникає попит на це обладнання.
Залежність між загальним ризиком акції, систематичним і
несистематичним ризиком виражається у такий спосіб: |
|
σ 2 = (β jσM )2 + (σe j )2 , |
(11.20) |
де σM – стандартне відхилення очікуваного прибутку на ринку; σej – стандартне відхилення похибки або шоку j-ої акції; β j – коефіцієнт β
j-ої акції.
Несистематичний ризик можна зменшувати шляхом ведення правильної інвестиційної політики фірми. Диверсифікація дозволяє знизити невизначеність отримання доходу шляхом придбання різних
344
фінансових інструментів. Тому несистематичний ризик називають ще
диверсифікованим ризиком.
Як бачимо, при управлінні підприємствами необхідно ретельно вивчати систематичний ризик і правильно управляти несистематичним.
11.7. Питання для самоконтролю
1.У чому полягає суть понять об’єктивна і суб’єктивна ймовірність?
2.Наведіть показники кількісного вимірювання величини ризику в абсолютному виразі.
3.Чому і в якому випадку для оцінювання переваг одного з декількох заходів використовують коефіцієнт варіації?
4.Наведіть показники кількісного вимірювання величини ризику в відносному виразі.
5.Чим відрізняються показники кількісного вимірювання в класичному і неокласичному підходах до оцінювання ризику?
6.Побудуйте криву розподілу ймовірностей отримання прибутку та зони ризику.
7.Яку криву називають кривою ризику?
8.Яка нерівність має виконуватися для того, щоб шанс банкрутства був не більше 1 з 9 випадків (розглянути різні ситуації інвестора)?
9.Що означають терміни систематичний і несистематичний ризики?
10.В чому суть коефіцієнта чутливості β?
11.Як класифікуються акції за ступенем ризику?
12.Як виражається залежність між загальним ризиком акції, систематичним і несистематичним ризиками?
345


