Лекція 18. Основи комбінаторики і теорії імовірностей

18.1. Елементи комбінаторики

Групи, що складені з яких-небудь елементів, називаються з’єднуючими.

Розрізняють три основні види з’єднань: розміщення, перестановки і сполучення.

Задачі, в яких здійснюється підрахунок можливих різних з’єднань, складених з кінцевого числа елементів за деяким правилом, називаються комбінаторними. Розділ математики, який займається їх розв’язання називається комбінаторикою.

1. Розміщення. Розміщеннями з елементів пов кожному називаються такі з’єднання, які відрізняються один від одного або елементами (хоча б одним), або порядком їх розташування.

Число розміщень з елементів попозначається символомі обчислюється за формулою

(18.1)

2. Перестановки. Перестановками з елементів називаються такі з’єднання з усіхелементів, які відрізняються одне від одного порядком розташування елементів.

Число перестановок з елементів позначається символом

Перестановки являють собою окремий випадок розміщення з елементів в кожному, тобто

або

(18.2)

Серед усіх перестановок з елементів рівне добутку послідовних чисел від 1 довключно. Добутокпозначають символом(читається «п-факторіал»), причому вважають причому рівність (16.2) можна переписати у вигляді

(18.3)

Використовуючи формулу (16.3), формулі (16.1) можна надати вигляду

(18.4)

При розв’язанні задач часто використовується рівність

(18.5)

Визначення. Сполученнями з елементів пов кожному називають з’єднання, які відрізняються одне від одного хоча б одним членом.

Сполучення з елементів попозначається. Вона знаходиться

(18.6)

Можна записати також у вигляді

(18.7)

або

(18.8)

Крім того, при розв’язанні задач використовуються наступні формули, що виражають основні властивості сполучень:

(18.9)

(за визначенням вважають і);

(18.10)

1. Знайти число розміщень: 1) з 10 елементів по 4; 2) з елементів по

Згідно з формулою (16.1), отримуємо:

1)

2)

2. Розв’язати рівняння

Використовуючи формулу (16.1), перепишемо рівняння у вигляді

Враховуючи, що розділимо обидві його частини натоді маємо

3. Скласти всі можливі перестановки з елементів 1) 2)

1) 3)

4. Обчислити значення виразів: 1) 2)

1)

2)

5. Обчислити: 1) 2)

Згідно з формулою (16.7), отримаємо:

1)

2)

6. Розв’язати систему рівнянь

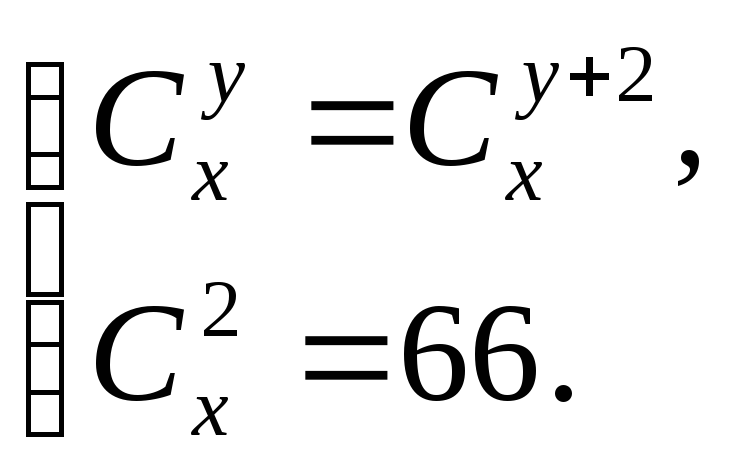
Розв’яжемо друге рівняння: Так яктоне задовольняє умові задачі.

Підставивши в перше рівняння системи, отримаємоВикористовуючи формулу (16.9), маємоТодіі, таким чином,звідкиТаким чином, отримуємо відповідь:

7. Знайти число розміщень: 1) 2)

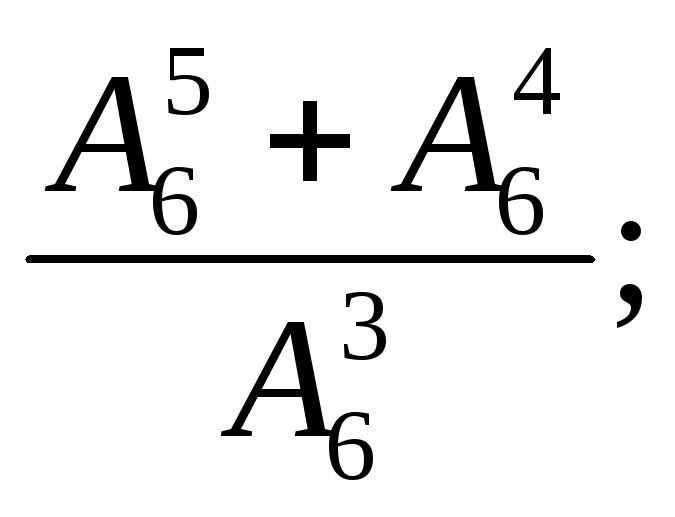8. Обчисліть: 1) 2)3)

9. 30 учнів обмінялися один з одним фотокартками. Скільки всього було роздано карток?

10. Розв’яжіть рівняння: 1) 2)3)

11. Розв’яжіть рівняння: 1) 2)3)

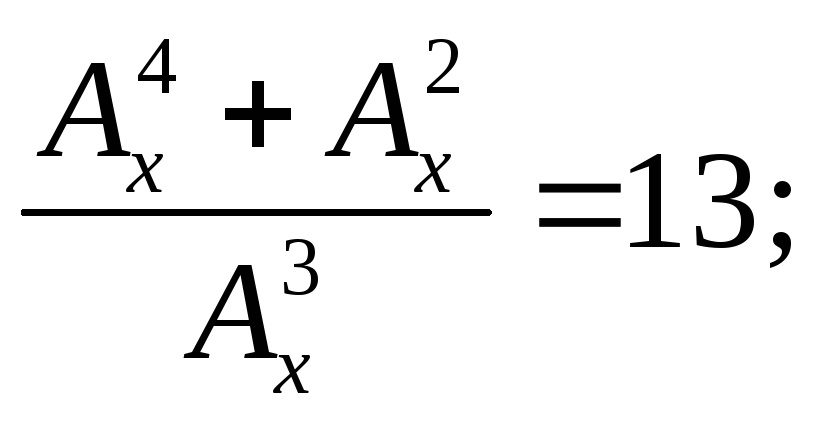12. Розв’яжіть рівняння: 1) 2)3)4)5)

13. Складіть усі можливі перестановки з літер:

14. Обчисліть значення наступних виразів: 1) 2)

15. Доведіть тотожності

1) 2)

16. Скоротіть дроби: 1) 2)3)

17. Виконайте дії:

1) 2).

18. Обчисліть: 1) 2)3)4)

19. Перевірте рівності:

1) 2)3)4)

20. Перевірте рівності: 1) 2)

21. Число сполучень з елементів по 3 в п’ять разів менше числа сполучень зелементів по 4. Знайти.

22. Скількома способами з 15 робочих можна складати бригади по 5 чоловік в кожній?

23. Розв’яжіть системи рівнянь:

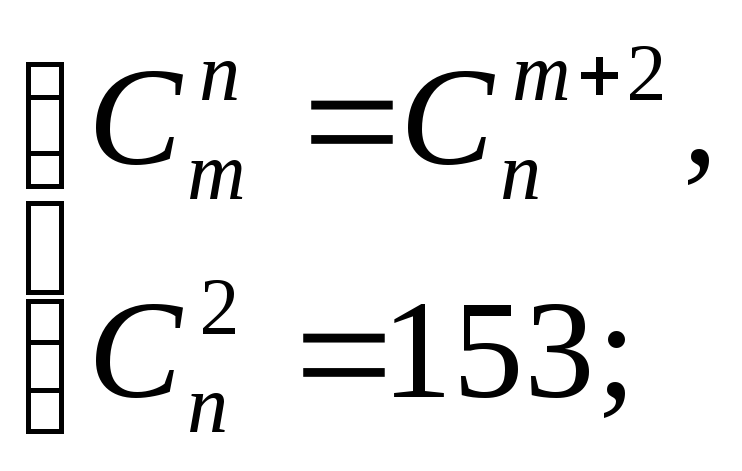1. 2)