Одесский национальный морской университет
Кафедра «Техническая кибернетика»
Курсовой проект (робота)
по дисциплине « Моделирование систем»
на тему: «Исследование динамических систем»
Студента : 3 курса 4 группы
Направление подготовки: 050101 – Компьютерные науки
Устича Артура Валентиновича
Руководитель:
ст. преп. Челабчи В.В.
Национальная шкала ________________
Количество балов: __________
Оценка: ECTS _____
Члени комиссии ________________ __ Челабчи В.В. __
(подпись) (ФИО)
________________ ________Челабчи В.Н. ___
(подпись) (ФИО)
________________ ___________________________
(подпись) (ФИО)
г. Одеса – 2013 год
СОДЕРЖАНИЕ
c.
1 ИДЕНТИФИКАЦИЯ ОБЫКНОВЕННОГО ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 1ГО ПОРЯДКА 3
1.1 Постановка задачи 3
1.2 Описание используемых методов 3
1.2.1 Аппроксимация на смежных отрезках 3
1.2.1 Аппроксимация на скользящих интервалах 4
1.3 . Результаты решения задачи идентификации. Проведение идентификации в среде Excel 6
1.4 Заключение 10
2 ИССЛЕДОВАНИЕ ДИНАМИКИ СИСТЕМЫ 11
2.1 Постановка задачи 11
2.2 Запись конечно-разностных аналогов дифференциальных уравнений 12
2.3 Запись конечно-разностных аналогов дифференциальных уравнений 12
2.4 Решение в среде Excel 13
15
2.4 Решение в среде Delphi 15
2.5 Заключение 19
ЛИТЕРАТУРА 20
ПРИЛОЖЕНИЕ 21
1 Идентификация обыкновенного линейного дифференциального уравнения 1го порядка
1.1 Постановка задачи
Существует физический объект, процесс в котором отражается параметром Y(τ). Величина Y изменяется во времени в зависимости от воздействия X(τ). Свойства объекта постоянны. Предполагается, что процесс в объекте описывается обыкновенным линейным дифференциальным уравнением первого порядка с постоянными коэффициентами:
,
(1.1)
где τ- время,
X(τ) - воздействие,
Y(τ) - реакция объекта,
А, K- коэффициенты, отражающие свойства объекта.
1.2 Описание используемых методов
1.2.1 Аппроксимация на смежных отрезках
Всю область изменения величин X(τ) и Y(τ) разбивается на участки, которые следуют друг за другом или перекрывают друг друга (Рис. 1.1).
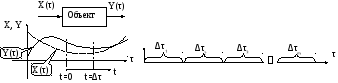
Рисунок.1.1 -
Схема разбиения области.
На каждом iомучастке
зависимость Y(
)
аппроксимируется полиномами невысоких
степеней вида:
, (1.2)
где
- локальная (в пределахiгоучастка) координата времени. Откуда:
,
(1.3)
Выражение для суммы квадратов невязок по всем рассмотренным зонам имеет вид:
,
(1.4)
где m – количество рассмотренных точек всей области определения функции (включая все выделенные интервалы), j– индекс точки.
Необходимым условием минимума функции Sявляется равенство нулю ее частных производных:
(1.5)
Откуда следует
(1.6)
Решив систему линейных алгебраических уравнений (1.6), получим значения A,K.