13

СОДЕРЖАНИЕ

c.

1 АППРОКСИМАЦИЯ ФУНКЦИИ ЗАДАННОЙ ТАБЛИЦЕЙ 2

1.1 Основы аппроксимации табулированной функции одного аргумента 2

1.2 Аппроксимация методом наименьших квадратов 2

2. РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 5

ПЕРВОГО ПОРЯДКА 5

2.1 Аналитическое решение 5

2.2 Численное решение (неявный метод) 5

2.3 Численноее ршение в среде Excel 5

1 Аппроксимация функции заданной таблицей

1.1 Основы аппроксимации табулированной функции одного аргумента

Аппроксимация - приближенное выражение математических объектов через другие, более простые (например, алгебраические или трансцендентные функции). Чаще всего для аппроксимации заданных табулированных функций используют формулы получаемые методом наименьших квадратов. Вид формулы задается, а коэффициенты формулы подбираются путем минимизации функционала, представляющего собой сумму квадратов невязок (квадратов разностей заданных значений функции и значений, полученных по аппроксимирующей формуле).

Суть аппроксимации заключается в том, что заданную таблично (табулированную) функциональную зависимость y=f(x) приближенно отражают (аппроксимируют) другой функцией (как правило, в виде аналитической зависимости), проходящей возможно ближе к точкам с координатами (x_i, y_i), но не требуют совпадения значений аппроксимирующей и табулированной функций в точках (x_i, y_i). При подобной аппроксимации чаще всего используется метод наименьших квадратов.

Для оценки состоятельности проведенной аппроксимации используется относительная оценка R²:

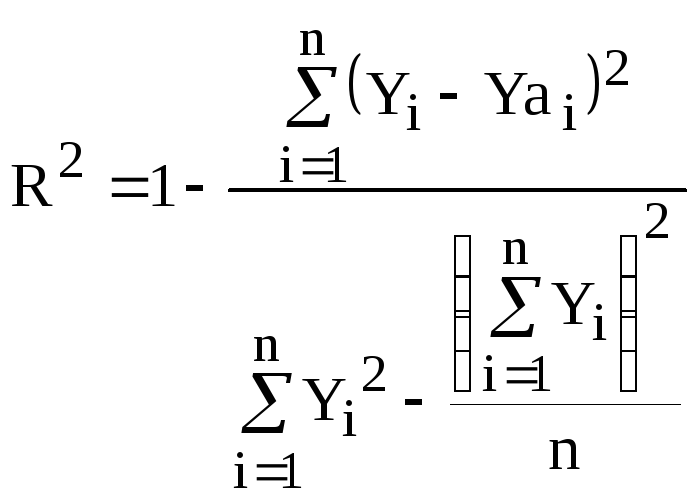(1.1)

Чем ближе значение R² к единице, тем лучше график аппроксимирующей функции согласуется с экспериментальными данными.

1.2 Аппроксимация методом наименьших квадратов

Таблица 1.1 – Аппроксимация МНК

i	X	Y	Y2	Ya	(Ya-Y)2
1	0,000	-1,768	3,126	-1,768	1,73E-09
2	0,100	-1,800	3,239	-1,800	2,45E-08
3	0,200	-1,751	3,068	-1,752	4,53E-08
4	0,300	-1,626	2,643	-1,625	1,84E-08
5	0,400	-1,427	2,036	-1,427	9,58E-08
6	0,500	-1,163	1,353	-1,163	1,5E-07
7	0,600	-0,845	0,715	-0,845	3,08E-08
8	0,700	-0,486	0,236	-0,486	1,23E-08
9	0,800	-0,099	0,010	-0,098	2,48E-07
10	0,900	0,300	0,090	0,300	7,07E-08
11	1,000	0,695	0,483	0,695	1,28E-07
12	1,100	1,070	1,145	1,070	1,16E-07
13	1,200	1,411	1,990	1,410	3,01E-08
14	1,300	1,702	2,898	1,703	4,85E-09
15	1,400	1,935	3,743	1,935	9,18E-09
16	1,500	2,098	4,402	2,098	3,49E-08
17	1,600	2,186	4,777	2,186	1,25E-08
18	1,700	2,194	4,812	2,194	1,72E-08
19	1,800	2,123	4,505	2,123	1,69E-08
20	1,900	1,975	3,900	1,975	2,04E-08
21	2,000	1,756	3,083	1,756	4,76E-09
22	2,100	1,476	2,177	1,475	5,51E-08
23	2,200	1,144	1,309	1,144	1,84E-08
24	2,300	0,775	0,600	0,775	6,95E-12
25	2,400	0,383	0,147	0,383	9,94E-09
26	2,500	-0,016	0,000	-0,016	6,22E-08
27	2,600	-0,407	0,166	-0,407	4,04E-13
28	2,700	-0,774	0,599	-0,773	3,46E-07
29	2,800	-1,101	1,213	-1,102	4,14E-08
30	2,900	-1,377	1,896	-1,377	2,01E-09
31	3,000	-1,590	2,528	-1,590	3,97E-08
32	3,100	-1,732	2,999	-1,732	3,07E-10
33	3,200	-1,796	3,226	-1,796	2,69E-08
34	3,300	-1,781	3,172	-1,781	9,24E-09
35	3,400	-1,687	2,846	-1,687	7,54E-12
36	3,500	-1,518	2,304	-1,518	6,39E-09
37	3,600	-1,280	1,639	-1,280	3,76E-08
38	3,700	-0,983	0,967	-0,983	1,09E-07
39	3,800	-0,640	0,409	-0,640	4,03E-07
40	3,900	-0,262	0,069	-0,262	8,04E-08

Аппроксимирующая функция:

.

Полученные коэффициенты функции

a=	0,200038
b=	2,000006
c=	2,000023
d=	-1,75003

Оценка эффективности аппроксимации

S=2,34Е-06

R²=1

где S- сумма квадратов невязок,

R² – оценка.

Результаты аппроксимации представлены на рис. 1.1.

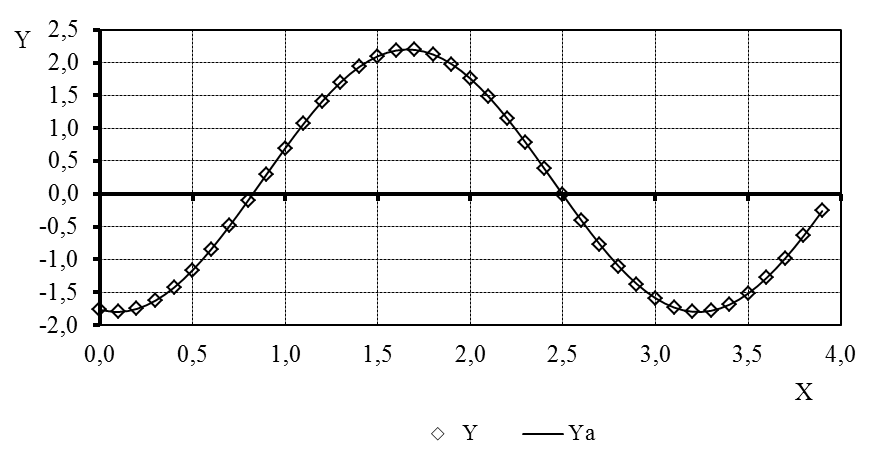
Рисунок 1 – Результаты аппроксимации