Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Справ_2013_08

.pdf

Скачиваний:

Добавлен:

11.02.2016

Размер:

31.43 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

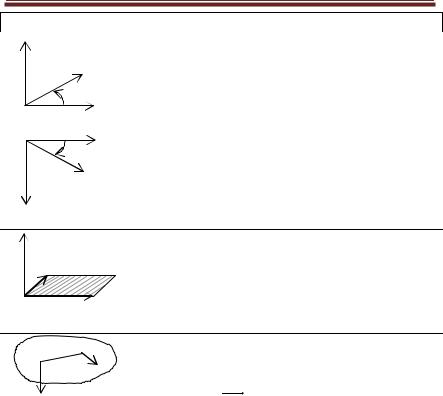
Производная

Асимптоты

Вертикальные асимптоты

Прямая x = a называется

Вертикальные асимптоты могут

вертикальной асимптотой

проходить лишь только через

графика функции y = f (x), если

точки разрыва графика функции

имеет место хотя бы одно из

y = f (x) или через граничные

равенств

точки области определения.

lim f (x)= ±¥

x®a +0

( x®a -0 )

Невертикальные асимптоты

Невертикальная асимптота –

Достаточное условие

существования невертикальной

это такая прямая y = kx + b , что

расстояние от т.

M (x, f (x))

асимптоты

Если существуют конечные пределы

графика функции y = f (x) до

k =

lim

f (x)

этой прямой стремится к 0, если

x ® +¥ (или x ® -¥ ).

x®+¥

( или x®-¥ )

При k ¹ 0 асимптоту называют

b =

lim

( f (x)- kx), то прямая

наклонной;

x®+¥

при k = 0 асимптоту y = b

( или x®-¥ )

y = kx + b есть асимптота графика

называют горизонтальной.

функции y = f (x) при x ® +¥

(или x ® -¥ ).

Найти асимптоты линии

f ( x ) =

2 x - 1

( x - 1 )2

Решение: 1) D( f ) = ( -¥;1 ) È( 1;+¥ )

lim f ( x ) = lim

2 x - 1

= +¥ Þ x = 1 − вертикальная асимптота

x®1

x®1 ( x - 1 )2

3) находим k =

lim

f ( x )

lim

2 x - 1

= 0

( x®-¥ )

( x®-¥ ) x( x - 1 )

®+¥

x®+¥

b =

lim

( f ( x ) - kx ) =

lim

2 x - 1

= 0

x ®+¥

( x

- 1 )

( x ®-¥ )

y = 0 − горизонтальная асимптота при x ® ±¥

Таблица интегралов

ò dx = x + c

ò sin xdx = - cos x + c

2. ò x

xa +1

+ c ,a ¹ -1

ò cos xdx = sin x + c

a + 1

= tgx+c

2.1

= 2

x + c

cos2 x

= -ctgx + c

2.2

= -

+ c

sin2 x

ò tgxdx = - ln

cos x

+ c

a x

ò a

+ c

10.

ò ctgxdx = ln

sin x

+ c

ln a

11.

= ln

+ c

3.1 ò e x dx = e x + c

sin x

4. ò

= ln

+ c

æ x

12.

= ln

tgç

+ c

cos x

è 2

4 ø

13. ò

×arctg

+ c

17. ò shxdx = chx + c

a 2 + x 2

14. ò

× ln

x - a

+ c

18. ò chxdx = shx + c

x 2 - a 2

x + a

15. ò

= arcsin x + c

19. ò

= thx + c

- x

20. ò

= -cthx + c

16. ò

= ln x +

+ m

+ c

sh2 x

x 2 + m

21.

a 2 + x 2 dx = x ×

a 2 + x 2

+ a 2

× ln x +

a 2 + x 2

+ c

22.

a 2 - x 2 dx = x ×

a 2 - x 2

+ a 2

× arcsin x + c

Формула Ньютона-Лейбница:

ò f ( x )dx = F( x )

= F(b )-F( a ) ,

F (x)= f (x)

Векторы

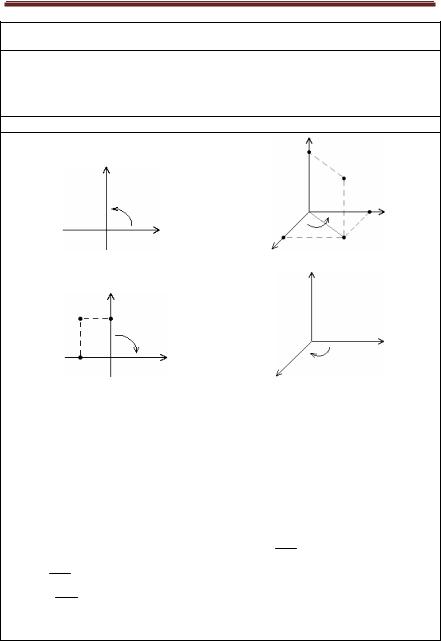
Прямоугольная декартовая система координат

Прямоугольная декартовая система координат на плоскости

(в пространстве) – это упорядоченная пара (тройка) взаимно перпендикулярных осей с общим началом отсчета – точкой О.

				Правая система координат
						z
		y				M z	M
							M

							M y
						0	y
0				x		M x
0				x		x
						x
				Левая система координат
						z
		x
		M	M x
		M y		y		0	x
		M y		y		y
0
				Координаты точки
		– направленный отрезок с началом в точке М1 и концом в точке М2.
	M1 M2
Величиной направленного отрезка						некоторой оси u
Величиной направленного отрезка					M1 M2	некоторой оси u
(обозначение: вел.				или M1 M 2 ) называют его длину, взятую со знаком
(обозначение: вел.			M1 M2	или M1 M 2 ) называют его длину, взятую со знаком

«плюс», если направление отрезка совпадает с направлением оси или его длину, взятую со знаком «минус», если направление отрезка противоположно направлению оси.

Координатами произвольной точки М в заданной системе координат называют

упорядоченную тройку чисел (x , y , z), где х = вел. OM x (абсцисса т. М),

у = вел. OM y (ордината т. М),

z = вел. OM z (аппликата т. М),

M x , M y и M z – ортогональные проекции т. М соответственно на оси Ох, Оу, Оz.

			Векторы
			Расстояние между двумя точками
d = A1 A2 = x2 - x1 , если точки A1 (x1 ) и A2 (x2 ) лежат на координатной
оси х.
d = M1M 2	=	(x2 - x1 )2 + y(2 - y1 )2 , если точки M1(x1 , y1 ) и M2 (x2 , y2 )
лежат на координатной плоскости xOy .
d = M1M2 = (x2 - x1 )2 + y(2 - y1 )2 + z(2 - z1 )2
для точек M1(x1 , y1 , z1 ) и M 2 (x2 , y2 ,z2 ).
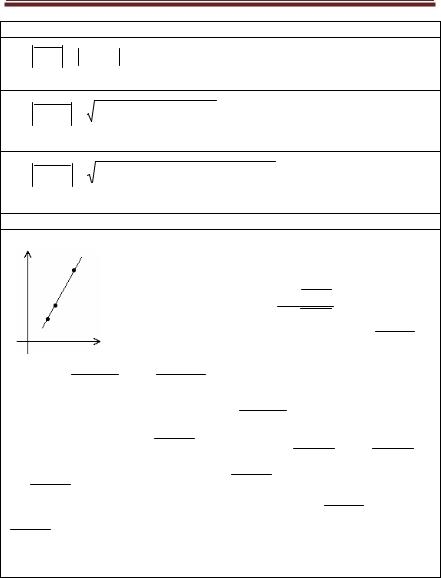
		Деление отрезка в данном отношении
y			Рассмотрим три точки M 1 (x1 , y1 ),	M 2 (x2 , y2 ) и
y			M (x, y), которые произвольно расположены на одной
	M 2		M (x, y), которые произвольно расположены на одной
	M 2		прямой.
			прямой.
M			Пусть известно число l = вел.M1M -		отношение,
M 1			вел.MM 2
0		x	в котором т. М делит направленный отрезок M 1 M 2 .
Тогда x = x1 + lx2			, y = y1 + ly2 .
	1 + l		1 + l
Для пространственного случая еще и z = z1 + lz 2 .
			1 + l
Если λ = 1, т. е. т. М делит M 1 M 2 пополам, то x = x1 + x2				,	y = y1 + y2 ,
z = z1 + z2			2		2
z = z1 + z2	(формулы деления отрезка M 1 M 2 пополам).
2
Если λ < 0, то это обозначает, что точка М находится вне M 1 M 2 , т.е. делит
M 1 M 2 внешним образом.
			54

			Векторы


			Понятие вектора

			r
Вектор – это направленный отрезок . Вектор a задан, если известны его
длина	r		r
длина	a	, а также углы a , b и g , которые a образует соответственно с осями
Ох, Оу, Oz.			r
cosa , cos b , cosg			принято называть направляющими косинусами a .

Коллинеарные векторы расположены на одной прямой или на параллельных прямых.

0 − нулевой вектор (начало и конец совпадают)

r	0	r	, если:	1)	r	= 1
a	0	− единичный вектор (орт) вектора a	, если:	1)	a	= 1
					r	r
				2) a		a

− орт оси Ох,

j − орт оси Оу,

k − орт оси Оz

Вектор ( -a ) противоположный вектору

a , если:

¯ -a

- a

éa

= b Û

Компланарные векторы расположены в одной плоскости или в

параллельных плоскостях.

Сложение ( вычитание) векторов

d = a + b ,

d =a

-b

Правило треугольника :

+ b

Векторы
Умножение вектора на число
r	r

Произведением вектора b на число l (или числа l на вектор b ) называют

такой вектор a

= lb , который удовлетворяет следующим условиям:

2) a

b , если l > 0 ;

¯ b , если l < 0 .

(!)

×a

Þ a

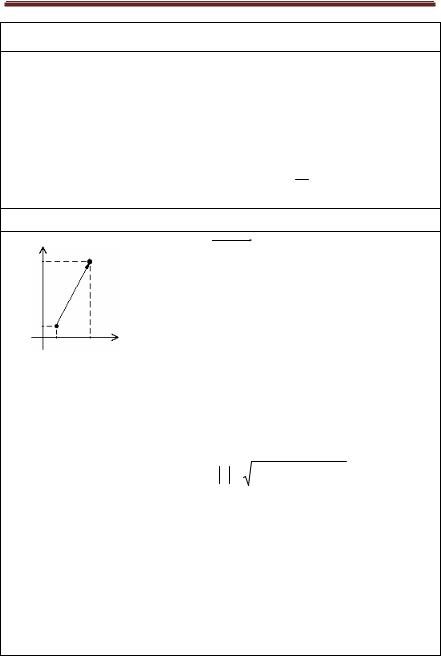
Координатная форма задания вектора

	y		M			Вектор	r	задан на плоскости хОу, если
			M			Вектор	a = M 1 M 2	задан на плоскости хОу, если
B 2	( y 2 )		2			известны координаты его начала и конца, т. е.
B 2	( y 2 )					известны координаты его начала и конца, т. е.
						M 1 (x1 , y1 ) и M 2 (x2 , y2 ).
B ( y )		M				Числа x2 - x1 = a x , y2 - y1 = a y , а также
B ( y )		M		x		z 2 - z1	= a z (для пространственного случая)
1	1	1		x		z 2 - z1	= a z (для пространственного случая)
	A ( x )		A	( x	)	называют координатами вектора				r
	A ( x )		A	( x	)	называют координатами вектора				a и записывают
r	1	1	2	r	2
r	= (a x , a y )		или	r	= (a x , a y , az ) (для пространственного случая). Такая
a	= (a x , a y )		или	a	= (a x , a y , az ) (для пространственного случая). Такая
									r
запись называется координатной формой задания a .

				r			r		r
				i = (1,0,0),			j = (0,1,0),		k = (0,0,1)

						r	r	a x	2 + a y 2 + az	2
			Длина вектора a :				a =	a x	2 + a y 2 + az	2

						r	r
				Если a = (a x ,a y ,az ), b = (bx ,by ,bz ), то

	r	r		ìa x = bx
1.	r	r	Û	ï
1.	a	= b	Û	ía y = by
				ï
				îaz = bz
	r	r

3. a ±b=(ax ±bx ,ay ±by ,az ±bz )

a y

b Û

= (l a x ,l a y ,l az )

4. l a

			Векторы

	Проекция вектора на ось
				r
	M 2	Проекцией вектора a = M 1 M 2 на ось u
r	M 2	называют величину направленного отрезка
a
a			A1 A2 оси u ( A1 и A2			- ортогональные
M1			A1 A2 оси u ( A1 и A2			- ортогональные
j	u	проекции точек M 1			и M 2 на ось u
A	A	соответственно)
1	2	соответственно)
				r	=	r	× cosj
				прu a	=	a	× cosj

Геометрический смысл координат вектора

Координаты вектора a есть проекции этого вектора на соответствующие координатные оси:

a y

az =

ax = прx a ,

= прy a ,

прz a

a x =

cosa

a y

cos b ,

cos g

0 = (cosa ,cos b ,cosg )

cos2a + cos2b + cos2g = 1

Разложение вектора по базису

Базисом на плоскости называют

Базисом в пространстве называют

упорядоченную пару

упорядоченную тройку

неколлинеарных векторов e1

и e2

некомпланарных векторов e1

, e2

и e3

– разложение вектора

= l1 e1 + l2

e2 + l3 e3

по базису ( e1

, e

2 , e3 );

(l1 , l2 , l3 ) – координаты вектора a

в базисе ( e1 , e2

, e3 )

Базис называют ортонормированным, если базисные векторы единичные и ортогональные.

r	r	r	r		r
a	= ax i + a y	j + az	k – разложение вектора		a
			r	r r
	по ортонормированному базису ( i ,			j , k )

Векторы

Скалярное произведение двух векторов

Скалярным произведением двух векторов			r	r
Скалярным произведением двух векторов			a	и b , которое обозначается
r r	r	r
(a b ) или a		×b , называется число равное произведению длин этих векторов

на косинус угла между ними, т.е.

r	r	r	r	cosj , где j − угол между векторами	r	r
r	r	r	r		r	r
a	×b =	a	b		a	и b .

Физический смысл скалярного произведения

Если под действием силы F материальная точка перемещается из начала в

конец вектора s , то работу A , произведенную этой силой, вычисляют

по формуле

A = F × s × cosj

или

A = F × s .

Так как

cosj = прbra

cosj = прarb , то

a × b =

прar b

или

× b =

прbr a ,

т. е. скалярное произведение двух векторов равно произведению длины одного из них на проекцию другого на направление первого.

Свойства скалярного произведения

×b = b ×

(переместительное);

l (a

×b )= la

×b = a

×lb (сочетательное);

+ b )c

= a ×c + b ×c (распределительное);

(скалярный квадрат вектора)

a ×a

= a

r 2

= a

a 2 ;

(a x

,a y ,az ) и

(bx ,by ,bz ), то

если a

b =

× b = a x bx + a y b y + a z bz ;

^ b

a ×b = 0

(необходимое и достаточное условие ортогональности двух векторов).

Неравенство Коши-Буняковского:	r	r	£	r	×	r
Неравенство Коши-Буняковского:	a	× b	£	a	×	b

Векторы

Векторное произведение двух векторов

Векторным

произведением двух

векторов a

и b ,

r r

которое обозначают [ a b

]

или a ´ b , называют такой

третий вектор

c , который удовлетворяет следующим

трем условиям:

r r

× sinj , где j =

æ r

Ù rö

a ´b

ça

, b ÷ ;

c ^ a , c ^ b ;

упорядоченная тройка векторов a , b , c - правая.

Геометрический смысл модуля векторного произведения

Модуль векторного произведения векторов a

и b

численно

равен

площади

параллелограмма,

построенного на векторах a

и b как на сторонах :

= Sпар-ма

´ b

Физический смысл векторного произведения

Пусть к точке М приложена сила F и пусть точка O –

некоторая

другая

точка

пространства(полюс).

Тогда

моментом силы F относительно точки O , называют

(F )

вектор mo (F )= OM ´ F .

Свойства векторного произведения

a ´ b = -b ´ a (антипереместительное);

(сочетательное);

l(a

´ b )= la

´ b = a ´ lb

(распределительное);

(a ´ b )´ c = a

´ c

+ b ´ c

a ´a = 0 ;

= (a x ,a y ,az ),

(bx ,b y ,bz ), то

a x a y

;

5. Если a

b =

a ´ b =

b y

a || b Û a

´ b = 0 (необходимое и достаточное условие коллинеарности

двух векторов) .

Векторы

Смешанное произведение трех векторов

r r r

Смешанным произведением трех векторов a , b и c , которое обозначают

r r r

ab c , называют число, равное скалярному произведению одного из них на векторное произведение двух других:

r r r

ab c

= (a

´ b )× c

, ab c

= a ×

(b ´ c ) и т. д.

Свойства смешанного произведения

1. Модуль смешанного произведения

трех векторов a ,

и c равен

объему V параллелепипеда,

построенного на перемножаемых

векторах как на ребрах,

исходящих из одной вершины:

V =

rrr

;

abc

r r r

> 0

– правая;

2. Если ab c

, то тройка векторов a

и c

r r r

< 0

– левая;

Если ab c

, то тройка векторов a

и c

Круговая перестановка не меняет знак смешанного произведения

r r r

ab c

= b ca = cab ;

4. (a

´ b )× c

= a

× (b ´ c );

Перестановка двух рядом стоящих векторов меняет знак смешанного

произведения:

r r r

r rr

r r r

rr r

ab c

= -b ac ,

b ca = -cb a ,

cab = -acb ;

= (c x ,c y ,cz ), то

Если a

(a x ,a y ,az ), b = (bx ,b y ,bz ), c

r r r

a x

a y

a z

b x

b y

;

ab c

c x

c y

c z

– компланарны Û

r r r

= 0 (необходимое и достаточное

a ,

b и c

ab c

условие компланарности трех векторов).

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в папке Справочники

#
11.02.201681.92 Кб21ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ.doc
#
11.02.2016357.89 Кб19Компл_числа.doc
#
11.02.201631.43 Mб27Справ_2013_08.pdf
#
11.02.2016115.71 Кб19таблицы_производ.doc