
Высшая Математика / Справочники / Справ_2013_08
.pdf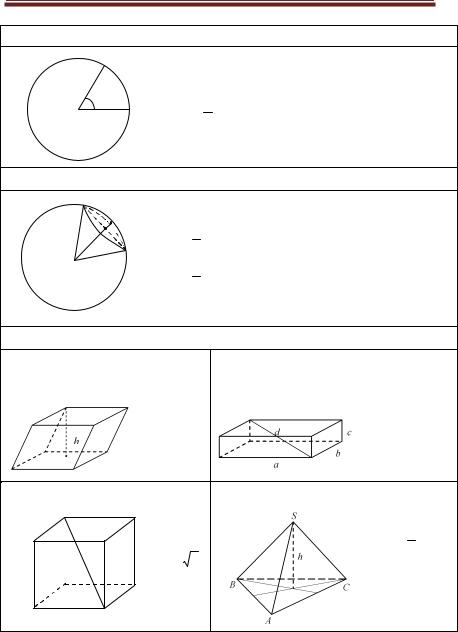
|
|
Геометрия |
|
||
|
Круг |
Окружность |
Сектор |
||
|
A |
С = 2pr |
(длина окружности) |
||
|
k |
Sкр = pr |
2 |
(площадь круга) |
|
|
r |
|
|||
|
a |
Sc = 1 r 2a |
(площадь сектора OAkBO) |
||
О |
B |
||||
|
|
2 |
|
|
|
|
|
l ÈАкВ = r ×a (длина дуги AkB), |
|||
|
|
|
а – радианная мера угла АОВ |
||
|
Шар |
Сфера |
|
Шаровой сектор |
|
|
|
S = 4pR2 |
(площадь поверхности сферы) |
||
R |
h |
V = 4 pR3 |
(объем шара) |
||
|
|
3 |
|
|
|
O |
|
V = 2 pR2h |
(объем шарового сектора), |
||
|
|
||||
|
|
3 |
|
h – высота шарового сегмента |
|
|
|
|
|
||
|
|
Многогранники |
|
||
Наклонный параллелепипед |
|
Прямоугольный параллелепипед |
|||
(все грани параллелограммы) |
|
(все грани прямоугольники) |
|||
|
|
V = Sосн × h |
|
|
V = abc |
|
|
|
|
|
d 2 = a2 +b2 +c2 |
|
Куб |
|
|
|
Пирамида |
(все грани квадраты) |
|
|
|
||
|
|
V = a 3 |
|
|
V = 1 Sосн ×h |
|
d |
d = a 3 |
|
|
3 |
|
|
|
|
||
a |
|
|
|
|
|
|
|
31 |
|
|
|
Функции и их графики
Понятие функции
Числовой функцией f называется такое отображение некоторого множества D действительных чисел на другое множество Е действительных чисел, при котором каждому числу x из D ставится в соответствие единственное
число y из Е.
Обозначение: y = f (x),
где х – аргумент функции f (независимая переменная), у – соответствующее значение функции f.
Символ f обозначает закон, по которому для любого х Î D можно найти y Î E.
Множество D называют областью определения функции f и обозначают D(f).
Множество Е называют областью значений функции f и обозначают E(f).
Определение. Графиком функции f называется множество точек (х, у)
координатной плоскости Оху таких, что хÎD ( f ), y = f (x).
Способы задания функции
|
Аналитический – функция |
|
Графический – функция задается с |
|||||||||
задаётся формулой (или |
|
|
помощью графика. |
|||||||||
несколькими формулами) |
|
|
|
|
||||||||
* |
|
|
ì - 2 x +1, x < -1 |
* |
|
|||||||
|
y = í |
x - 2, |
x ³ -1 |
|
||||||||
|
|
î |
|
|
||||||||
|
|
|||||||||||
Табличный – функция задается с |
Словесный – функция задается |
|||||||||||
помощью таблицы, |
|
|
|
словесным описанием. |
||||||||
устанавливающей соответствие |
* |
Значение функции равно |
||||||||||
между значениями аргумента и |
||||||||||||
единице, если x –рациональное число и |
||||||||||||
значениями функции: |
|
|
|
|||||||||
|
|
|
равно нулю, если x – иррациональное |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
число (функция Дирихле). |
||
|
x |
|
x1 |
|
x2 |
|
… |
xn |
|
|
|
|
|
y |
|
y1 |
|
y2 |
|
… |
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32

Функции и их графики
Основные элементарные функции
1. |
линейная функция: |
y = kx + b, |
k , b Î R |
|
|
2. |
степенная функция: |
y = xa , |
a Î R |
|
|
3. |
показательная функция: y = a x , a > 0, a ¹ 1 |
||||
4. |
логарифмическая функция: |
y = loga x , |
a > 0, a ¹ 1 |
||
5. |
тригонометрические функции: |
y = sin x, y = cos x, y = tgx, y = ctgx |
|||
6. |
обратные тригонометрические функции: |
y = arcsin x, y = arccos x , |
|||
|
|
|
|
|
y = arctgx , y = arcctgx |
Элементарные функции
Элементарная функция получается из конечного числа основных элементарных функций с помощью конечного числа арифметических операций и операции композиции (нахождение функции от функции).
|
Например: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
целая рациональная функция: y = Pn (x), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
где P (x)= a |
|
xn + a |
|
xn-1 + ... + a |
|
x + a |
|
, a |
|
¹ 0, a |
|
|
Î R, i = |
|
|
||||||||||
|
0 |
1 |
n-1 |
n |
0 |
i |
0,n |
|||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. |
дробная рациональная функция: |
y = R(x), где R(x) = |
Pn (x) |
|
|
, Qm (x) ¹ 0 |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
3. |
гиперболические функции: |
|
|
|
|
|
|
|
|
|
|
Qm (x) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
- |
синус гиперболический y = sh x |
, где sh x = |
e x |
- e - x |
|||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
- |
косинус гиперболический |
у = сhx , где сhx = |
|
e x + e- x |
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh x |
|
|
|
|
|
|
||||||
|
- |
тангенс гиперболический |
y = th x , где thx = |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ch x |
|
|
|
|
|
|
|
||||
|
- |
котангенс гиперболический |
y = сth x , где сthx = |
сh x |
|
|||||||||||||||||||||
|
sh x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
ch2 x - sh2 x = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
sh2x = 2shx×chx |
|
|
|
|
sh(x ± y)= shx ×chy ± chx × shy |
|||||||||||||||||||
|
|
ch2 x = ch2 x + sh2 x |
|
|
ch(x ± y)= chx ×chy ± shx × shy |
|||||||||||||||||||||
33
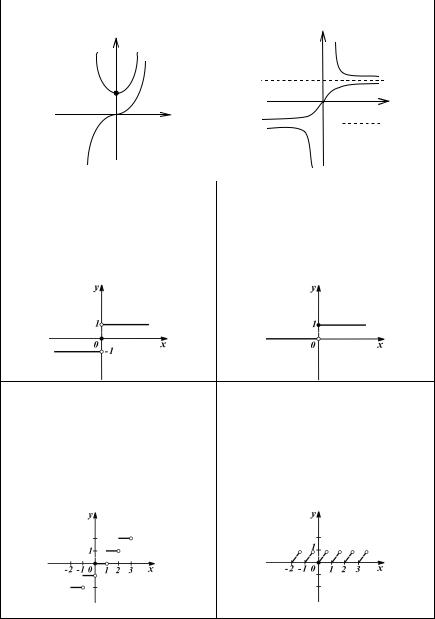
|
Функции и их графики |
|
|
|
||
|
|
|
|
|||
|
Графики гиперболических функций |
|
|
|||
|
|
|
|
|
|
|
|
y |
|
y |
|
|
|
|
y = chx |
|
|
y= cthx |
|
|
|
|
|
|
|
|
|
|
1 |
y =s h x |
у=1 |
|
y= thx |
|
|
|
|
|
|||
|
|
0 |
x |
|
||
|
0 |
x |
|
|
||
|
|
|
у= -1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неэлементарные функции |
|
|
|
|
|
y = sign x |
|
Единичная функция Хевисайда |
|
||
|
Символ sign x читаем: сигнум x, т.е. |
|
|
|
|
|
|
знак x |
|
|
)º íì1, x ³ 0 |
|
|
|
ì1, |
x > 0 |
y = h(x |
|
||
|
ï |
x = 0 |
|
|||
|
y = sign x º í0, |
|
î0, |
x < 0 |
|
|
|
ï |
x < 0 |
|
|
|
|
|
î-1, |
|
|
|
|
|
Символом [ x ] обозначают |
Символом { x } о бо з н ач а ю т |
||
наибольшее целое число, не |
р а з н о с т ь м е ж д у ч и с л о м x и |
||
превышающее числа х. |
его целой частью, т.е. {x}= x − [ x]. |
||
|
|
||
* [0,5]=0 |
[ − 0 ,3]= − 1 |
* { 1 , 2 } = 1 , 2 − 1 = 0 . 2 |
|
{ 5 , 4 } = 5 , 4 − 5 = 0 . 4 |
|||
[ 3 , 5 7 ] = 3 |
[ − 1 , 5 ] = − 2 |
||
Фун кц ия y = [x] (читаем: целая |
Фун кц ия y = {x} (читаем: дробная |
||
часть x) |
|
часть x) |
|
34

Функции и их графики
Общие свойства функций
Нули и промежутки знакопостоянства
Нуль (корень) функции f – это то значение аргумента, при котором значение функции f равно нулю (точка пересечения графика с осью Ox).
Промежутки знакопостоянства функции f – это такие промежутки из
D( f ), на которых все значения функции f только положительны или только отрицательны.
На промежутке знакопостоянства график функции расположен либо выше оси абсцисс (функция положительна) либо ниже оси абсцисс (функция отрицательна).
Четность, нечетность
Функция f называется четной, если:
1)D ( f ) симметрична относительно точки O;
2)для любых х Î D ( f ) выполняется равенство f(− x) = f(x).
График четной функции симметричен относительно оси
ординат.
Функция f называется нечетной, если:
1) D ( f ) симметрична относительно точки O;
2)для любых х ÎD ( f ) выполняется равенство f(− x) = − f(x).
График нечетной функции симметричен относительно начала координат.
Периодичность
Функция f называется
периодической с периодом Т > 0,
если для любого х Î D( f ) значения (x ±T ) Î D( f ) и, кроме того, выполняется равенство
f ( x ±T ) = f ( x ) .
Наименьший положительный период функции f называют ее
основным периодом и
обозначают T0 .
Если функция y = f ( x ) периодическая с основным периодом T0 , то функция y = f( ω x ), ω Î R также является
периодической с периодом T = T0 .
|
|
|
|
|
|
ω |
||||
* |
y = sin5 x |
Þ T = |
2p |
= |
2 |
|
p |
|||
|
|
|
|
|||||||
|
|
5 |
|
5 |
|
|
||||
* |
у = tg(2px) |
Þ T = |
p |
= |
1 |
|
||||
2p |
|
|||||||||
|
|
|
|
2 |
|
|||||
35
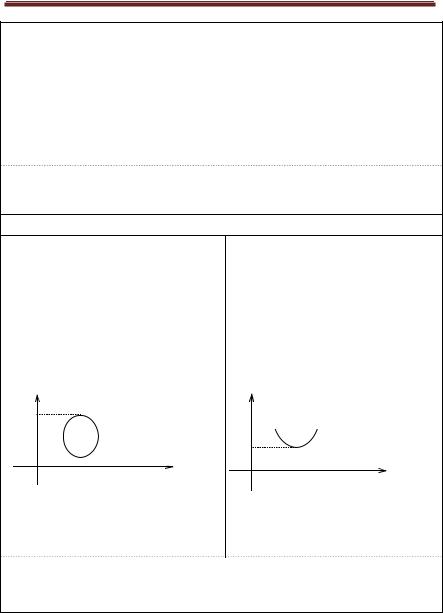
Функции и их графики
Монотонность
Функция f называется |
Функция f называется |
возрастающей на ( a , b ), если для |
убывающей на ( a , b ), если для |
любых x1 и x 2 из ( a , b ), |
любых x1 и x 2 из ( a , b ), |
удовлетворяющих неравенству |
удовлетворяющих неравенству |
x 2 > x1 , выполняется неравенство |
x 2 > x1 , выполняется неравенство |
f ( x 2 ) > f ( x1 ) . |
f ( x 2 ) < f ( x1 ) . |
|
|
Интервалы возрастания или убывания функции f называют интервалами ее монотонности, а саму функцию f называют монотонной на каждом из них
Экстремумы
Точка a из области определения функции f называется точкой максимума этой функции, если для всех x из достаточно малой окрестности этой точки выполняется неравенство f ( a ) >f ( x ) .
Значение функции f в точке максимума называется максимумом этой функции.
y
f(a) |
|
xmax=a |
||
|
ymax=f(а) |
|
||
|
|
|
||
|
|
|
|
|
|
|
|
x |
|
0 |
a |
|
||
В точке максимума возрастание функции сменяется ее убыванием.
Точка b из области определения функции f называется точкой минимума этой функции, если для всех x из достаточно малой окрестности этой точки выполняется неравенство f ( b ) <f ( x ) .
Значение функции f в точке минимума называется минимумом этой функции.
y
xmin=b ymin=f(b)
f(b)
0 |
b |
x |
В точке минимума убывание функции сменяется ее возрастанием.
Точки максимума и минимума называют точками экстремума функции f, а значения функции f в точках экстремума называют экстремумами функции f .
36

Функции и их графики
Обратные функции
Пусть функция у = f (х) производит отображение множества D на множество Е.
Обратное отображение множества Е на множество D, при котором каждому y ÎЕ соответствует единственное число x ÎD , называется
обратной функцией f -1 .
Для взаимно обратных функций f и f -1 :
D ( f ) = E( f -1) , E( f ) = D ( f -1) .
Обратную функцию можно построить только для монотонной функции.
Построение формулы |
|
Построение графика |
|
обратной функции |
|
обратной функции |
|
1) равенство y =f ( x ) р а з р е ш и т ь |
Чтобы построить график функции |
||
относительно переменной x, т. е. |
|||
|
-1 |
||
найти x = f -1( y ) ; |
f |
, надо график функции f |
|
2) в равенстве x = f -1( y ) заменить x |
подвергнуть преобразованию |
||
на y, а y на x, т.е. записать |
симметрии относительно прямой |
||
y = x . |
|||
y = f -1( x ) . |
|||
|
|
|
|
ðДля функция y = x2 , x ≥ 0 построить обратную функцию.
1) Разрешим равенство y = x2 , x ≥ 0
относительно x. Получим x = y .
2)Заменим x на y и y на x. Получим y =  x .
x .
37

Функции и их графики
Графики основных элементарных функций
Линейная функция y = kx+b, D(y)=R
|
|
|
y |
|
|
|
|
y |
|
|
|
y |
|
|
|
|
y |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
|
b |
a |
||||||
|
|
|
0 |
|
|
|
|
|
0 |
b x |
|
|||||||||||||
|
|
|
|
|
x |
0 |
x |
|
|
|
|
|
|
|
|
|
|
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
b |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=tga<0 |
|
|
k=tga<0 |
|||||||
|
|
k=tga>0 |
|
k=tga>0 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
b<0 |
|
b>0 |
|
|
b<0 |
|
|
|
|
|
b>0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Общая степенная функция y = xa , a Î R , |
D(y)= R+ |
|||||||||||||||||
|
Степенная функция |
|
|
|
Степенная функция с целым |
|||||||||||||||||||
|
с натуральным показателем |
|
|
|
отрицательным показателем |
|||||||||||||||||||
|
y = xn , n Î N , D(y)= R |
|
|
|
y = x -n , a = -n , n Î N , |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(y)= (- ¥;0)È (0;+¥) |
||||||||||
* |
|
|
|
y = x2 |
|
|
|
* |
y = x -2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
0 1 |
x |
|
|
|
-1 |
0 |
1 |
|
|
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Степенная функция с дробным показателем |
|
|||||||||||||||
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
y = x 3/2 |
|
y |
|
|
y = x 1/2 |
y |
|
|
|
|
y = x -1/2 |
||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
x |
|
0 |
|
|
x |
0 |
|
|
|
|
|
x |
|||||||
|
1 |
|
1 |
1 |
|
|
||||||||||||||||||
38
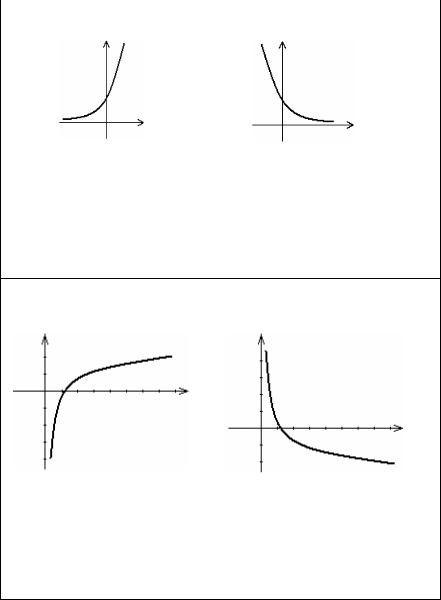
|
|
|
|
Функции и их графики |
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
Показательная функция y = ax, a > 0, a¹ 1 |
|
||||||
|
|
|
a > 1 |
|
|
|
|
0 < a < 1 |
|
|
|
|
|
y |
|
|
|
y |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
|
|
|
0 |
x |
|
|
1) D(y)=R, |
E(y)=R+ |
1) D(y)=R, |
E(y)=R+ |
|
|
||||
|
2) |
x 2 > x1 <=> a x 2 |
> a x 1 |
2) |
x 2 |
> x1 <=> ax2 < a |
x 1 |
|
||
|
3) |
lim a x |
= +¥ |
|
3) |
lim |
a x |
= 0 |
|
|
|
|
x®+¥ |
|
|
|
x ® +¥ |
|
|
|
|
|
|
lim a x = 0 |
|
|
|
|
|
|||
|
|
|
|
lim |
a x = +¥ |
|
|
|||
|
|
x ® -¥ |
|
|
|
x®-¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Функцию y = ex называют экспоненциальной, а её график – экспонентой.
|
|
Логарифмическая функция y =loga x, |
a >0, a ¹1 |
||||||||
|
|
|
a > 1 |
|
|
|
|
|
|
0 < a < 1 |
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
0 |
1 |
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
||
1) D(y)=R+ , |
E(y)=R |
|
|
|
+ |
|
E(y)=R |
||||
2) |
x 2 > x1 <=> loga x 2 > loga x1 |
|
1) D(y)=R , |
|
|||||||
|
2) |
x 2 > x1 <=> loga x 2 < loga x1 |
|||||||||
3) |
lim |
log |
a x |
= +¥ |
|
3) |
lim |
log |
a |
x = -¥ |
|
|
x ® +¥ |
|
|
|
|
|
x ® +¥ |
|
|
|
|
|
lim |
log |
a x |
= -¥ |
|
|
lim |
log |
a |
x |
= +¥ |
|
x ® + 0 |
|
|
|
|
|
x ® +0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функцию y = log e x называют логарифм натуральный и обозначают y= ln x.
39

Функции и их графики
Тригонометрические функции
Функция синус: y = sin x |
|
Функция косинус: y = cos x |
|||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
- |
3π |
y |
|
π |
3π |
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
-π |
0 |
|
π |
2π |
x |
|
|
|
|
0 |
|
|
|
|
x |
|||||||||
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
1) |
D(y)=R |
|
|
|
|
|
1) |
D(y)=R |
|
|
|
|
|
|
|||||||||||
2) |
E(y)=[−1;1] (функция синус |
2) |
E(y)=[−1;1] (функция косинус |
||||||||||||||||||||||
|
ограниченная) |
|
|
|
|
|
|
ограниченная) |
|
|
|
|
|
||||||||||||
3) |
sin(−x) = − sin x (нечётная) |
3) |
cos(−x) = cos x (чётная) |
|
|
||||||||||||||||||||
4) |
T =2π (основной период) |
|
4) |
T0 =2π (основной период) |
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
lim sinx не существует |
|
5) |
lim cosx не существует |
|||||||||||||||||||||
|
x®±¥ |
|
|
|
|
|
|
|
|
|
|
|
x®±¥ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Функция тангенс: y = tg x |
|
Функция котангенс: y = ctg x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
x |
|
|
-π 0 |
|
π 2π x |
||||||||
- |
3π |
- |
π π |
3π |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) |
D(y): x ≠ |
p |
+πn, nÎZ |
|
1) |
D(y): x ≠ πn, nÎZ |
|
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) |
E(y)=R (функция тангенс |
2) |
E(y)=R (функция котангенс |
||||||||||||||||||||||
неограниченная) |
|
|
|
|
|
неограниченная) |
|
|
|
|
|
||||||||||||||
3) |
tg(−x)= − tg x (нечётная) |
|
3) |
сtg(−x)= − сtg x |
(нечётная) |
||||||||||||||||||||
4) |
T0 =π (основной период) |
|
4) |
T0 =π (основной период) |
|||||||||||||||||||||
5) |
lim |
tg x = -¥ |
|
|
|
|
|
5) |
lim ctgx = +¥ |
|
|
|
|
|
|
||||||||||
|
x® |
p |
+0 |
|
|
|
|
|
|
|
|
|
|
|
x®+0 |
|
|
|
|
|
|
||||
|
2 |
|
tg x = +¥ |
|
|
|
|
|
|
lim ctg x = -¥ |
|
|
|
|
|
||||||||||
|
lim |
|
|
|
|
|
|
x®-0 |
|
|
|
|
|
|
|||||||||||
|
x® |
p |
-0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
