
Высшая Математика / Справочники / Справ_2013_08
.pdf
Арифметика и алгебра
Проценты
Процентом называется сотая часть числа, т.е. 1% = 0,01.
Чтобы число процентов выразить в виде дроби, достаточно число процентов разделить на 100:
5% = |
5 |
|
= 0 ,05 |
|
|
|
30% = |
30 |
= 0 ,3 |
|
|
||||||||
|
|
|
|
|
|
||||||||||||||
100 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|||||
|
Основные типы задач на проценты |
||||||||||||||||||
Нахождение p % от числа a |
|
ð |
Найти 40 % от 200. |
||||||||||||||||
a - 100 % |
|
|
|
|
|
|
a × p |
|
|
|
|
|
|
40 × 200 |
|||||
x - p % |
|
|
|
x = 100 |
|
|
|
|
x = |
|
|
|
|
= 80 |
|||||
|
|
|
|
|
|
100 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нахождение числа |
|
ð |
3 % вклада в сбербанк |
||||||||||||||||
|
составляют 150 грн. Какова сумма |
||||||||||||||||||
по его проценту |
|
||||||||||||||||||
|
вклада? |
|
|
|
|
|
|||||||||||||
a - p% |
|
|
x = a ×100 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x-100% |
|
|
|
|
|
|
p |
|
|
x = |
150 ×100 |
= 5000 (грн.) |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
Нахождение процентного |
|
ð |
При плановом задании 50 |
||||||||||||||||
|
автомобилей в день завод выпустил 55 |
||||||||||||||||||
отношения двух чисел |
|
||||||||||||||||||
|
автомобилей. На сколько процентов он |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
a - 100 % |
|
x = |
p |
|
выполнил план? |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
× 100% |
|
|
55 × 100 |
|
|
|||||||||
p - x % |
|
a |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
x = |
|
|
= 110 % |
|||||||
|
|
|
|
|
|
|
|
|
|
50 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Формула сложных процентов |
|
|
|
|
|
|
|
|
|
|
|
||||||||
æ |
|
|
|
p |
|
ön |
|
ð |
Вкладчик положил в банк |
||||||||||
Аn = A × ç1 |
+ |
|
|
|
÷ , |
|
|||||||||||||
è |
|
|
100 ø |
|
|
20000 грн. под 14% годовых. Сколько |
|||||||||||||
А – первоначальная величина |
|
денег будет на счете вкладчика через 3 |
|||||||||||||||||
вклада; |
|
|
|
|
|
|
|
|
года? |
|
|
|
|
|
|
|
|
|
|
n – срок вклада; |
|
|
|
|
|
|
|
|
A3 = 20000(1 + 0,14)3 = 29630,88 (грн.) |
||||||||||
p – ежегодно начисляемое число |
|
||||||||||||||||||
процентов; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аn – величина вклада через n лет. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|

Арифметика и алгебра
Числовые неравенства
Если |
a - b > 0 , |
Если a - b < 0 , |
Если |
a - b = 0 , |
|
то |
a > b |
то |
a < b |
то |
a = b |
|
|
|
|
|
|
Свойства
1.Если a > b , то b < a
2.Если a > b и b > c , то a > c
3. |
Если a > b , то êéac > bc, |
c > 0 |
|
ëac < bc, |
c < 0 |
4. |
Если a > b , то a + c > b + c, c Î R |
|
5. |
Если a > b, c > d ( a,b,c,d > 0 ) , то ac > bd |
|
6.Если a > b и c > d , то a + c > b + d
7.Если a > b и c < d , то a - c > b - d
8. |
Если a > b |
( a > 0, b > 0 ) , то an > bn , n Î N |
||||
9. |
Если a > b |
( ab > 0 ) , то |
1 |
< |
1 |
|
a |
||||||
|
|
|
|
b |
||
ð Доказать, что a +b ³ ab, a ³ 0, b ³ 0.
2
Доказательство. Составим разность между левой и правой частями неравенства и установим ее знак:
a + b - ab = a + b - 2 ab = ( a - b )2 . |
||
2 |
2 |
2 |
Очевидно, что ( a -
a -  b )2 ³ 0.
b )2 ³ 0.
2
Следовательно, неравенство справедливо.
12

|
|
|
|
|
|
|
|
|
Арифметика и алгебра |
|
||||
|
|
|
|
|
|
|
|
Степени действительных чисел |
|
|||||
|
|
Определения |
|
|
|
|
Свойства |
|
||||||
1. |
|
an = a ×a ×K×a |
|
|
|
|
|
|
||||||
|
|
|
|
|
14243 |
1. ar1 × ar2 = ar1 +r2 |
6. 1r =1 |
|
||||||
|
|
|
|
|
|
|
|
n |
|
|||||
n Î N , n ¹ 1, a Î R |
r1 |
|
|
|
|
|
||||||||
2. |
|
|
a1 = a, |
a Î R |
2. ar = ar1 |
-r2 ,a ¹ 0 |
7. 0r = 0, r > 0 |
|
||||||
|
|
a 2 |
|
|
|
|
|
|||||||
3. |
|
a 0 = 1, a ¹ 0 |
3. (ar1 )r2 = ar1 ×r2 |
8. (-1 k) = íì+1, k = 2n,n ÎN |
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
-n |
|
|
|
|
|
î-1, k = 2n -1 |
||||
4. |
|
|
a |
|
|
= an , |
4. (a × b)r = ar × br |
9. (- a)2n > 0, a > 0 |
||||||
|
|
|
a ¹ 0, n Î N |
æ a |
ör |
a r |
|
|
||||||
|
|
m |
|
n |
|
m |
|
5. ç |
÷ = |
b |
r |
10. (- a)2n-1 < 0, |
a > 0 |
|
5. |
a |
n |
= |
a |
, a ³ 0 |
è b |
ø |
|
||||||
|
|
|
r ,r1 ,r2 Î R ,b ¹ 0 |
|
|
|||||||||
n Î N , n ¹1, m Î N |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||
6. |
|
- m |
= |
|
1 |
,a > 0 |
|
|
|
|
|
|
||
a |
n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n am |
|
|
|
00 – не имеет смысла |
|
|||
n Î N , n ¹1, m Î N |
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Формулы сокращенного умножения |
|
|||||
(a ± b)2 = a 2 ± 2ab + b2 |
|
a 2 - b2 = (a - b)(a + b) |
квадрат суммы и разности двух чисел |
разность квадратов |
|
|
|
|
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac |
|
|
|
|
|
(a ± b)3 = a3 ± 3a2b + 3ab2 ± b3 |
– куб суммы и разности |
|
|
|
|
a3 ± b3 = (a ± b)(a2 m ab + b2 ) |
– сумма и разность кубов |
|
Формула |
бинома |
Ньютона |
(a + b)n = an + nan-1 × b + |
n(n - |
1) |
an-2b2 + |
n(n -1)(n - 2) |
an-3b3 + ... + bn |
|
|
|
|||
1× 2 |
1× 2 ×3 |
|
|||
13

Арифметика и алгебра
Корни n-й степени
Корнем n-й степени из действительного числа а называется такое число b,
n-я степень которого равна а, т.е. |
n a = b Û bn = a, n ÎN , n ¹ 1 |
|||
|
|
|
|
|
Если а >0, то: |
|
|
Принято считать, что символу |
|
1. |
2n+1 a > 0 |
|
|
|
|
|
2 n a , а >0, соответствует только |
||
2. |
2n+1 - a < 0 |
|
|
|
|
|
одно положительное значение. |
||
|
|
|
|
|
3. |
2n - a – не существует |
|
Его называют арифметическим. |
|
|
n 0 = 0 |
2 a = a |
|
|
|
|
|
|
|
Арифметические корни
Арифметическим корнем n-й степени из числа а ( a ³ 0 ) называют неотрицательное число b, n-я степень которого равна а
1. (n |
|
)n = a, a ³ 0 |
Свойства |
|
|
|||||||
|
4. n m a = nm a , a ³ 0 |
|||||||||||
a |
||||||||||||
2. (n am )k = n a mk , a ³ 0 |
5. n ab = n a n b, a ³ 0, b ³ 0 |
|||||||||||
3. |
n |
a |
m |
= |
nk |
a |
mk |
, a ³ 0 |
a |
= |
n a |
|
|
|
|
|
|
6. n |
, a ³ 0, b > 0 |
||||||
|
|
|
|
|
|
|
|
|
|
b |
|
n b |
|
|
|
|
|
|
|
|
|
|
Следствия |
|
|
1. |
|
a2 = a , a Î R |
4. x ×2n a = 2n x2n ×a , x > 0, a ³ 0 |
|||||||||
2. 2n a2n = a , a Î R |
5. x × 2n a = -2n x2n × a , x < 0, a ³ 0 |
|||||||||||
3. 2n+1 a2n+1 = a, a Î R |
6. n am ×r as = nr amr+sn , a ³ 0 |
|||||||||||
14

Арифметика и алгебра
Логарифмы
Логарифмом числа b (b > 0) по основанию a (a > 0, a ¹ 1) называется показатель степени, в которую надо возвести основание a, чтобы получить b.
Обозначение: loga b ,
b – подлогарифмическое выражение, a – основание логарифма.
log10 a = lg a – десятичный логарифм loge a = lna – натуральный логарифм
aloga b = b, |
a > 0, |
|
|
|
a ¹1, |
|
b > 0 (основное логарифмическое тождество) |
||||||||||||||
В частности: |
elnb = b, |
b > 0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
loga a = 1, |
a > 0, |
|
|
|
a ¹ 1 |
(логарифмическая единица) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
loga 1 = 0, |
a > 0, |
|
|
a ¹ 1 |
(логарифмический ноль) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства |
|
|
|
||||
1. |
logc (ab)= logc a + logc b, |
c > 0, |
c ¹ 1, |
a > 0, |
b > 0 |
||||||||||||||||
2. |
log |
|
æ a ö |
= log |
|
|
a - log |
|
b, |
c > 0, |
c ¹ 1, |
a > 0, |
b > 0 |
||||||||
|
ç |
÷ |
|
|
|
||||||||||||||||
|
|
c |
è b ø |
|
c |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
||
3. |
log |
|
ak = k ×log |
|
a, |
c > 0, |
c ¹ 1, |
a > 0 |
|
|
|
||||||||||
|
c |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
logb a = |
logc a |
|
, |
|
c > 0, c ¹ 1, a > 0, |
b > 0, |
b ¹ 1 |
|||||||||||||
logc b |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. |
logb a × loga b = 1 или logb a = |
1 |
|
, |
a > 0, |
a ¹ 1, b > 0, b ¹ 1 |
|||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
loga b |
|
|
|
|
||
6. |
logbn a |
m |
m |
|
|
|
|
|
|
a > 0, b > 0, |
b ¹ 1 |
|
|
||||||||
|
= n logb a , |
|
|
||||||||||||||||||
15

Арифметика и алгебра
|
Сравнение степеней |
|
Сравнение корней |
||||
1. |
Если a > b ³ 0 и r > 0 , |
1. |
Если a > b ³ 0 , то n a > n b |
||||
|
то ar |
> br |
|
||||
|
|
|
|
||||
2. |
Если a > b > 0 и r < 0 , |
2. |
Если a >1, то 1 < n a < a |
||||
|
то a |
r |
< b |
r |
|
||
|
|
|
|
|
|
||
3. |
Если a >1 |
и r2 > r1 , |
3. |
Если 0 < a <1, то a < n a < 1 |
|||
|
то ar2 > ar1 |
|
|||||
|
|
|
|
||||
4. |
Если 0 < a <1 и r2 > r1 , |
4. |
n a + b £ n a + n b , a ³ 0,b ³ 0 |
||||
|
то ar2 |
< ar1 |
|
|
|
||
Сравнение логарифмов
1. |
Если x2 > x1 > 0 и a >1, то loga x2 > loga x1 |
|
|
||||||||||
2. |
Если x2 > x1 > 0 и 0 < a <1, то loga x2 < loga x1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Средние величины и их сравнение |
|
|||
1. |
|
a + b – среднее арифметическое двух чисел |
(a > 0, |
b > 0) |
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
(a > 0, |
b > 0) |
2. |
|
|
|
ab |
– среднее геометрическое двух чисел |
||||||||
3. |
|
|
|
2 |
|
|
– среднее гармоническое двух чисел |
(a > 0, |
b > 0) |
||||
|
|
1 |
+ 1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
a |
|
|
|
|
|
|
|
|||||
|
|
|
b |
|
|
|
|
|
|
|
|||
4. |
|
|
|
a2 + b2 |
– среднее квадратическое двух чисел |
(a > 0, b > 0) |
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
a £ |
2 |
1 |
£ ab £ a + b £ a 2 + b 2 |
£ b (a > 0 , b > 0 , a £ b ) |
||||||
|
|
|
|
1 |
+ |
2 |
2 |
|
|
|
|||
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16

Арифметика и алгебра
Прогрессии
Арифметическая |
Геометрическая |
|
|
÷ a1 ,a2 ,a3 ,K |
÷÷ b1 ,b2 ,b3 ,K |
an+1 = an + d , n Î N |
bn+1 = bn ×q, n Î N |
a1 – первый член прогрессии |
b1 ¹ 0 – первый член прогрессии |
d – разность прогрессии |
q ¹ 0 – знаменатель прогрессии |
|
|
Свойства
an =a1 +d( n -1) |
|
|
|
|
|
b = b qn-1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|||
характеристическое свойство |
характеристическое свойство |
|||||||||||||||||||||
a = |
an-1 + an+1 |
|
|
|
|
|
b 2 = b |
n-1 |
×b |
n+1 |
||||||||||||
|
|
|
||||||||||||||||||||
n |
|
|
2 |
|
|
|
|
|
|
|
|
n |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сумма первых n членов |
|
|
сумма первых n членов |
|||||||||||||||||||
|
|
a1 |
+ an |
|
|
|
|
|
|
|
|
|
b (1 - qn ) |
|
|
|||||||
Sn = |
×n |
|
|
|
Sn = |
1 |
|
|
|
|
|
, q ¹ 1 |
||||||||||
1 - q |
|
|
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Sn = b1 × n, q = 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
формула для разности |
формула для знаменателя |
|||||||||||||||||||||
прогрессии |
|
|
|
|
|
|
|
прогрессии |
||||||||||||||
d = an+1 - an |
|
|
|
|
|
|
|
q = |
|
bn +1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
bn |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
если n + m = k + p , то |
|
|
если n + m = k + p , то |
|||||||||||||||||||
a +a =a +a |
p |
|
|
|
|
bn × bm = bk ×bp |
||||||||||||||||
n m |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||||||||||||
сумма последовательных |
если |
|
q |
|
<1, то прогрессия |
|||||||||||||||||
|
|
|||||||||||||||||||||
натуральных чисел от 1 до n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
бесконечно убывающая и ее сумма |
||||||||||||||||||||||
|
|
|
n(n +1) |
|
|
|||||||||||||||||
S = |
|
|
|
|
|
|
|
|
S = |
b 1 |
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
1 - q |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17

Арифметика и алгебра
Многочлен n-й степени от одной переменной
P |
(x)= a xn + a xn-1 + ...+ a |
n-1 |
x + a |
n |
, |
a |
¹ 0, a |
i |
Î R, i = |
0, n |
|
|
n |
0 |
1 |
|
|
0 |
|
|
|
|
|||
P (x)= ax2 + bx + c, a ¹ 0, b ¹ 0, c ¹ 0 |
– квадратный трехчлен |
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
P1(x)= ax + b, |
a ¹ 0, b ¹ 0 |
|
|
|
|
– линейный двучлен |
||||||
Если Pn (x0 )= 0 , то x0 – корень многочлена Pn (x)
Делимость многочленов
Разделить многочлен Pn (x ) на многочлен Qm (x) (n ³ m )– это значит найти такие многочлены M n -m (x) и R(x ), для которых выполняется равенство Pn (x)= Qm (x)× Mn-m (x)+ R(x).
Теорема Безу. Остаток от деления многочлена Pn (x ) на двучлен x -a равен Pn (a ).
Следствие. Если x = x0 есть корень многочлена Pn (x ), то многочлен
Pn (x ) делится нацело на x - x0 .
Наибольшее число действительных корней многочлена Pn (x ) совпадает с его степенью n, причем, в этом случае:
Pn (x)= a0 (x - x1 )(x - x2 )...(x - xn )
В частности: ax2 + bx + c = a(x - x1 )(x - x2 )
Алгебраические уравнения
Алгебраическим уравнением n-й степени с одним неизвестным называют уравнение вида
a0 x n + a1 x n -1 + ... + an -1 x + an = 0, a0 ¹ 0, ai Î R, i = 0, n
Если алгебраическое уравнение n-й степени с целыми коэффициентами имеет целые корни, то они содержатся среди делителей свободного члена
18

Арифметика и алгебра
Квадратное уравнение ax2 + bx + c = 0, a ¹ 0
x |
= - b ± |
D , |
где D = b2 |
- 4ac – дискриминант квадратного трехчлена |
|||||||||||||||||||||||||||||||||||||||||
1,2 |
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Если D > 0 , то |
|
|
|
|
|
|
|
Если D = 0 , то |
|
|
|
|
|
|
|
Если D < 0 , то |
|
|
|||||||||||||||||||||||||||
x1 ¹ x2 (корни |
|
|
|
|
|
|
|
|
x1 |
= x2 |
= - |
|
b |
|
|
(корни |
|
|
|
уравнение |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действительных |
||||||||||||||||||||||||
действительные и |
|
|
|
|
|
2a |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корней не имеет |
|
|
|||||||||||||||||||||||||
разные) |
|
|
|
|
|
|
|
|
|
|
действительные и |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
равные) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Частные случаи квадратного уравнения |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
ax 2 + 2kx + c = 0 |
|
|
|
|
|
|
|
x 2 + px + q = 0 (приведенное |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
квадратное уравнение) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
x1,2 = - k ± k 2 - ac |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x1,2 = - |
p |
± |
|
p 2 |
|
- q |
|
|
|
||||||||||||||||||||||||||
|
|
D |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||
|
|
= k |
2 |
- ac |
³ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
= p |
2 |
|
- q ³ |
0 |
|
|
|
|
|
|
|||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема |
Виета |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Если x2 + px + q = 0 , то |
|
|
|
|
|
|
|
|
|
Если |
|
ax 2 + bx + c = 0 , то |
||||||||||||||||||||||||||||||||
|
|
ì x |
1 + x 2 = - p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï x1 + x 2 = - |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|||||||||||||||||||||||||
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
î x 1 × x 2 = q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï x1 × x 2 |
|
= |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выделение полного квадрата |
|
из квадратного трехчлена |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
æ |
|
|
|
b |
|
|
|
c |
ö |
æ |
|
|
|
|
|
|
|
b |
|
|
|
b2 |
|
|
|
|
b2 |
|
|
|
c |
ö |
|
|
|
|
|||||
ax2 + bx + c = a ç x2 |
+ |
|
|
x + |
|
÷ = aç x2 |
+ |
2 |
|
|
|
x + |
|
|
|
- |
|
|
|
|
+ |
|
|
÷ = |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
è |
|
|
|
a |
|
|
|
a |
ø |
ç |
|
|
|
|
|
|
2a |
4a |
|
|
|
|
4a |
|
|
|
a |
÷ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|||||||||||||||
|
æ |
b ö |
2 |
|
æ c |
|
|
|
b2 ö |
æ |
|
b |
ö |
2 |
|
|
4ac - b2 |
|
|
|
æ |
|
|
|
|
b ö |
2 |
D |
|||||||||||||||||
= a ç x + |
|
÷ |
+ a |
ç |
|
- |
|
|
|
÷ = a ç x + |
|
|
|
|
÷ |
+ |
|
|
|
|
|
|
= a ç x + |
|
|
|
÷ |
- |
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
è |
2a ø |
|
|
ç |
|
|
|
4a |
÷ |
è |
|
2a ø |
|
|
|
|
4a |
|
|
|
|
è |
|
|
|
|
2a ø |
|
4a |
|||||||||||||||
|
|
|
è a |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
19
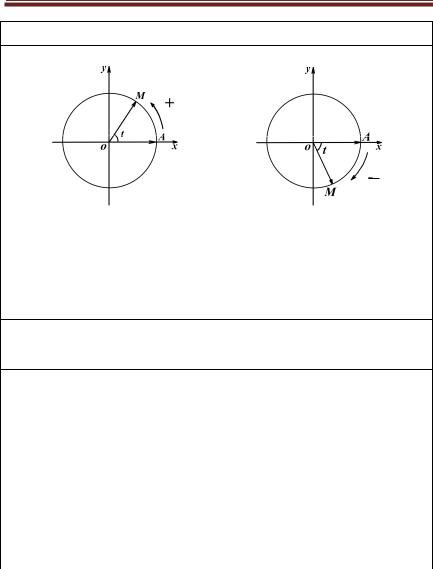
Тригонометрия
Понятие угла в тригонометрии
Углом (в тригонометрии) называют меру поворота подвижного радиусавектора относительно положительного направления оси Ох.
Если поворачивать радиус-вектор из исходного положения по часовой стрелке, то угол поворота t < 0, а если против часовой стрелки, то угол поворота t > 0
t Î(- ¥; + ¥)
Полный угол – это мера минимального поворота, при котором конечное положение радиуса – вектора совпадает с исходным
Углы измеряют в градусах и радианах
1 градус – это центральный угол, |
1 радиан – это центральный угол, |
|||||||
составляющий 1/360 часть полного |
опирающийся на дугу окружности, |
|||||||
угла. |
|
|
|
|
длина которой равна радиусу этой |
|||
Полный угол содержит 360 о |
окружности. |
|||||||
Полный угол содержит |
||||||||
|
|
|
|
|
||||
1° – один градус |
|
|
¢ |
|
|
|
|
|
1° = 60 |
|
|
2p R |
= 2p » 6,28 радиан |
||||
¢ |
¢ |
= 60 |
¢¢ |
|
|
|||
|
|
|
||||||
1 – одна минута |
1 |
|
|
|
R |
|||
¢¢ |
1° = 3600 |
¢¢ |
|
|||||
1 – одна секунда |
|
|
|
|
||||
20
