Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Справ_2013_08

.pdf

Скачиваний:

Добавлен:

11.02.2016

Размер:

31.43 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Прямая на плоскости

Основные уравнения прямой на плоскости

Прямая, проходящая через точку M0 (x0 , y0 )

r ( )

перпендикулярно вектору n = A;B :

A(x - x0 )+ B (y - y0 )= 0

r	= (A; B)
n	= (A; B)
(l)	M0 (x0 , y0 )

Общее уравнение прямой:

Ax + By + C = 0

Частные случаи общего уравнения прямой

Прямая проходит через начало координат:

Ax + By = 0

Ось y -ов:

x = 0

Ось x -ов:

y = 0

x = a

y = b

x = a

y = b

Уравнение прямой с угловым коэффициентом:

(l)

y = kx + b, k = tga

Прямая проходит через начало координат:

y = kx

Прямая, проходящая через т.М 0

в заданном направлении

(l)

(если k – фиксированное), или пучок прямых, проходящих

M 0 (x0 , y0 )

через т. М 0 :

y - y0 = k(x - x0 )

Уравнение прямой

Прямая, проходящая через две

«в отрезках на осях»: (l)

заданные точки M1 (x1 , y1 )и M2 (x2 , y2 ):

= 1

x - x1

y - y1

2 - x1

y2 - y1

a b

Угол между двумя прямыми

= (A1

,B1 )

1. (l1 ): A1 x + B1 y +C1 = 0, n1

×n

(l2 ): A2 x + B2 y +C2

= 0, n2 = (A2 ,B2 )

cosj =

× n

2. (l1 ): y = k1 x +b1

k1 - k2

tgj =

1 + k1k2

): y = k x +b

(l1 )|| (l2 ):

k1 = k2

(условие параллельности)

(l1 )^ (l2 ):

k2 = -1 / k1

(условие перпендикулярности)

Плоскость

Основные уравнения плоскости

Плоскость, проходящая через точку M0 (x0 , y0 , z0 ),

перпендикулярно вектору	r
перпендикулярно вектору	n = (A;B;C ):
A(x - x0 )+B(y - y0 )+C(z -z0 )= 0		w

r	= (A, B, C )
n

M 0 (x0 , y0 , z0 )

Общее уравнение плоскости: Ax + By + Cz + D = 0

Частные случаи общего уравнения плоскости

Плоскость проходит через начало координат:

Ax+ By +Cz = 0

Плоскость параллельна той оси, название

Ax + By + D = 0

Ax + Cz + D = 0

которой отсутствует в уравнении:

By + Cz + D = 0

Плоскость

yOz :

x = 0

Плоскость параллельна той

x = a

Плоскость

xOz :

y = 0

координатной плоскости,

y = b

название которой

Плоскость

xOy :

z = 0

z = c

отсутствует в уравнении:

Уравнение плоскости

Уравнение плоскости, проходящей

«в отрезках на осях»:

через три фиксированные точки

M1 (x1 , y1 , z1 ) , M2 (x2 , y2 ,z2 ), M3 (x3 , y3 , z3 ):

x - x1 y - y1 z - z1

= 1

a	b	c	0	b y	x2 - x1	y2 - y1	z2 - z1 = 0

x a	x3 - x1 y3 - y1 z3 - z1

Угол между двумя плоскостями

(w1 ): A1 x + B1 y + C1 z + D1 = (w2 ): A2 x + B2 y + C2 z + D2 =

cosj =

n1 × n2

или

||) w(

: )

r	= (A1 , B1 ,C1 )
0, n1	= (A1 , B1 ,C1 )
r	= (A2 , B2 ,C2 )
0, n2	= (A2 , B2 ,C2 )
cos j	=	A1 A2 + B1 B2 + C1C 2
cos j	=	+ B 2	+ C 2	× A2	+ B 2	+ C 2
	A2	+ B 2	+ C 2	× A2	+ B 2	+ C 2
	1	1	1	2	2	2

(условие параллельности)

(w1 )^ (w2 ): A1 A2 + B1 B2 + C1C2 = 0 (условие перпендикулярности)

Прямая в пространстве

Основные уравнения прямой в пространстве

Общие уравнения прямой:

(l ): ìí A1 x + B1 y + C1z + D1 = 0, îA2 x + B2 y + C2 z + D2 = 0,

r		= (A1 , B1 ,C1 )					w1	(l)
n1
r		= (A , B		,C		)		w2
n	2		2		2
		2

Канонические уравнения прямой:

M 0 (x0 , y0 , z0 )

(l)

x - x0

y - y0

z - z0

(m, n, p)

S =

Уравнение прямой, проходящей через

две фиксированные точки

Параметрические уравнения прямой:

M1 (x1 , y1 , z1 )

и M2 (x2 , y2 ,z2 ):

ìx = x0 + mt

M1(x1, y1, z1 )

(l)

= y0 + nt

í y

M2 (x2 , y2 , z2 )

= z0 + pt

î z

x - x1

y - y1

z - z1

x2 - x1

y2 - y1 z2 - z1

Угол между двумя прямыми

(l ):

x - x1 =

y - y1 = z - z1 , S = (m ,n , p )

r r

S1 × S

cosj =

x - x2

y - y2

z - z2

= (m

)

, S

,n , p

Угол между прямой и плоскостью

(l ): x - x0 = y - y0 = z - z0 , S = (m ,n, p)
			r
m	n	p	r
			r
(w): Ax + By + Cz + D = 0, n = (A, B,C )
	r	r
	S × n		, q +j = p
sin j = cos q = r		r	, q +j = p	w
	S × n		2	w

r
n	(l)	r
n	(l)
r
		S
q	j
	j

Кривые линии в декартовых и полярных координатах

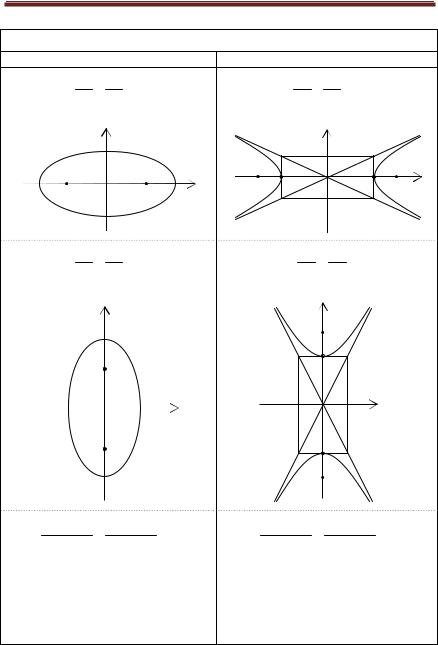
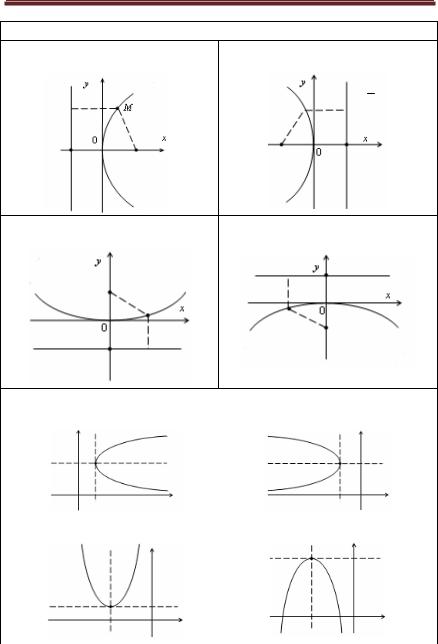
Кривые 2–го порядка (канонические уравнения)

Эллипс

Гипербола

y 2

= 1

x 2

y 2

= 1

a 2

a2 - b2 = c2 , a ³ b > 0

a 2 + b 2 = c 2 , a > 0, b > 0

B2 (0;b )

А1 (- а;0)

А2 (а;0)

А1

А2

F1 (- с;0)

(с;0 )

F1 (- с;0 )

F2 (с;0 )

B1 (0;-b)

y 2

= 1

x 2

a 2

= 1

b 2 - a 2 = c 2 , b ³ a > 0

a 2 + b 2 = c 2 , a > 0, b > 0

F2 (0; с )

B2 (0;b )

F2 (0; с )

А1 (- а;0)

А2 (а;0)

A1 (- a;0)

A2 (a;0 )

F1 (0;-с )

B1 (0;-b)

F1(0;-с)

(x - x0 )2

(y - y0 )2

(x - x0 )2

(y - y0 )2

= 1

a 2

= 1

a 2

Оси эллипса проходят через его

Оси гиперболы проходят через её

центр (x0,y0)

параллельно осям

центр (x0,y0) параллельно осям

координат.

Кривые линии в декартовых и полярных координатах

Парабола

y2 = 2 px, p > 0

y2 = -2 px , p > 0

х = р

	p					æ		p		ö
x = -		æ p				F ç	-		;0	÷
					ö	F ç	-	2	;0	÷
					ö	è		2		ø
2		Fç		;0	÷
2		Fç	2	;0	÷
		è	2		ø

x2 = 2 py, p > 0					x 2 = -2 py,	p > 0
							у =		р
æ		p ö						2
æ		p ö
F ç	0;		÷
F ç	0;	2	÷
è		2	ø
					æ		p ö
					Fç	0;-		÷
					è		2	ø
			у = -	р
			2

Парабола с вершиной в т. С (х0,у0)

(y - y0 )2 = 2 p(x - x0 )			(y - y0 )2 = -2 p(x - x0 )
y				y
	C		C
O	x		O	x
(x - x0 )2 = 2 p(y - y0 )			(x - x0 )2 = -2 p(y - y0 )
	y		C	y
	C		O	x
	O	x

Кривые линии в декартовых и полярных координатах

Параметрические уравнения линий в декартовых координатах

Циклоида

Полукубическая парабола

= t

= a(t

- sint )

ïx

Û y

= x

ïx

, a > 0

- cost )

ïy = t 3

ïy = a(1

2pa

Астроида

ïx = a cos

, a > 0

= t

ïx

Û y

3 = x 2

î y = a sin

= t

îy

Окружность		Эллипс		Гипербола
ìx = R cost	,	ìx = a cost	,	ìx = a cht
í	,	í	,	í	,
î y = R sint		î y = b sint		î y	= b sht
R > 0		a > 0, b > 0		a > 0, b > 0
0 £ t < 2p		0 £ t < 2p		-¥ < t < +¥

Кривые линии в декартовых и полярных координатах

Уравнения кривых в полярных координатах

Полярная система координат на плоскости задается некоторой точкой О, называемой полюсом, и осью Op, называемой полярной осью.

Полярными координатами точки M называют упорядоченную пару чисел (r ;j ), где r = OM – полярный радиус точки M (расстояние от полюса О до точки M), j – полярный угол точки M (угол между полярной осью и

направленным отрезком OM ).

Если совместить полярную систему координат с декартовой прямоугольной системой координат так, чтобы полюс совпал с началом координат, а полярная ось – с положительным направлением оси Ox , то получим формулы, устанавливающие связь между этими двумя системами координат:

	x = r cosj , y = r sinj .

Кардиоида	Лемниската Бернулли
r = a(1 + cosj) , a > 0	r = a cos2j , a > 0

Окружность

x 2 + y 2 - ax = 0 Û r = a cosj

x 2 + y 2 - by = 0 Û r = b sinj

æ a

b ö

C ç

, R

, a

> 0

C ç

, R =

, b > 0

è 2

2 ø

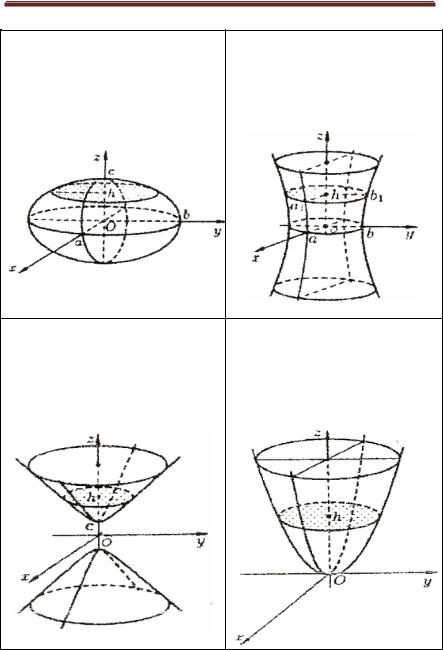
Поверхности 2-го порядка

Эллипсоид

Однополостный гиперболоид

x 2

y 2

z 2

x 2

y 2

z 2

= 1 ,

a 2

b 2

c 2

a 2

b 2

c 2

a > 0, b > 0, c > 0

Двуполостный гиперболоид							Эллиптический параболоид
	x 2	+	y 2	-	z 2	= -1,		x 2	+	y 2	= z,
	a 2		b 2
					c 2			2 p		2 q
	a > 0, b > 0, c > 0							p > 0, g > 0

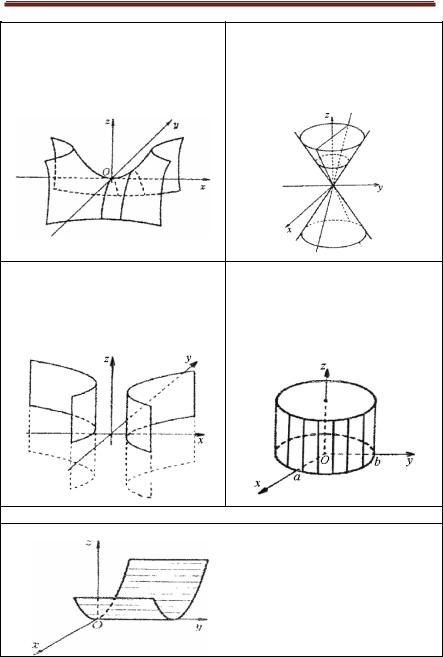
Поверхности 2-го порядка

Гиперболический параболоид

Конус 2-го порядка

x 2

y 2

= z,

= 0 ,

2 p

p > 0, g > 0

a > 0, b > 0, c > 0

Гиперболический цилиндр					Эллиптический цилиндр
	x 2		y 2			x 2		y 2
		-		= 1 ,			+		= 1 ,

	a 2		b 2			a 2		b 2
	a > 0, b > 0					a > 0, b > 0

Параболический цилиндр

x 2 = 2 pz ,

p > 0

Комплексные числа

Понятие комплексного числа

Комплексным числом z (КЧ z) называется выражение вида z = x + i y ,

где х и у – действительные числа, i – так называемая мнимая единица, определяемая равенством i 2 = - 1 .

Эту форму записи комплексного числаz называют алгебраической. При этом число x называют действительной частью комплексного числа z и обозначают Re z (от латинского realis – действительный), а число y называют мнимой частью комплексного числаz и обозначают Im z (от латинского imaginarius – мнимый).

Заметим, что при y = 0 получают частный случай комплексного числа–

действительное число x, а при x = 0 – чисто мнимое число y i .

Множество всех комплексных чисел обозначают С.

Алгебраическая форма комплексного числа z

Определения

Действия

z 2 = x 2 + iy 2

z1 ± z2 = ( x1 ± x2 ) + i( y1 ± y2 )

z1 = x1 + iy1

z1 × z2 = (x1 x2 - y1 y2 )+ i (x1 y2 + x2 y1 )

def

ìx

= x

z × z = x

+ y

z1 = z2 Û

î y1

= y2 þ

+ y

+ i

- x

сопряженное КЧ:

z 2

x 22

+ y 22

x 22

+ y22

= x - iy

Для комплексных чисел понятия «больше» и «меньше» не установлены!

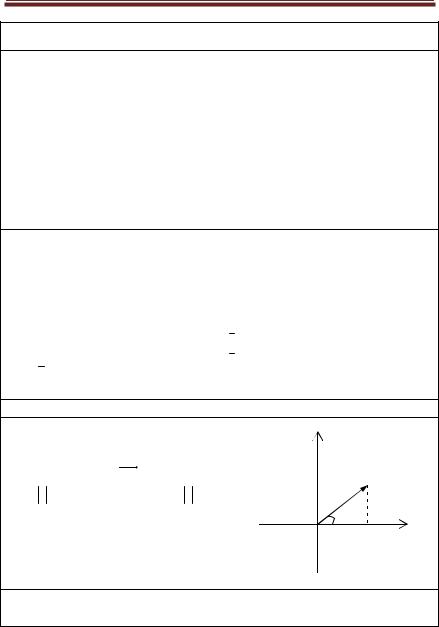
Геометрическое представление комплексных чисел

КЧ z – это точка М(x, y)

ось х-ов – действительная ось ось y-ов – мнимая ось

КЧ z – это вектор OM :

r = z – модуль КЧ z , 0 < z < +¥;

j = Argz – аргумент КЧ z,

-¥ < Argz < +¥ ;

argz – главное значение аргумента КЧ z ,

-p < arg z £ p.

M(x,y)

r y

	j
O	x	x

Тригонометрическая форма комплексного числа z: z = r(cosj + i sinj )

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в папке Справочники

#
11.02.201681.92 Кб21ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ.doc
#
11.02.2016357.89 Кб19Компл_числа.doc
#
11.02.201631.43 Mб27Справ_2013_08.pdf
#
11.02.2016115.71 Кб19таблицы_производ.doc