теория вероятности

ЛЕКЦИЯ 1.

Тео́рия вероя́тностей— раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероя́тность (вероятностная мера) —численная мера возможности наступления некоторого события.

Один из разделов теории вероятности это комбинаторика. Характерная примета в задачах из области комбинаторики – вопрос в них обычно можно сформулировать так, чтобы он начинался со слов: «Сколькими способами...».

Элементы комбинаторики

Пусть есть множество, которое состоит из n элементов. Обозначим его

Un.

Перестановкой из n элементов называется заданный порядок во множестве Un.

Примеры перестановок:

1)распределение n разных должностей среди n людей; 2)распределение n разных предметов в одном ряду.

Сколько разных перестановок можно образовать во множестве Un? Число перестановок обозначается Pn (читается Р из n).

Чтобы вывести формулу числа перестановок, представим себе n ячеек, пронумерованных числами 1,2...n. Все перестановки будем образовывать, располагая элементы Un в этих ячейках. В первую ячейку можно занести каждого из n элементов (иначе: первую ячейку можно заполнить n разными способами). Заполнив первую ячейку, можно n-1 способом заполнить вторуя ячейку (иначе: при каждом способе заполнение первой ячейки находится n-1 способов заполнения второй ячейки). Таким способом существуют n(n-1) способов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти n-2 способов заполнения третьей ячейки, откуда получаем, что три ячейки можно заполнить n(n-1)(n-2) способами. Продолжая этот процесс, получим, что число способов заполнения n ячеек равняется

n n 1 n 2 ...321. Отсюда

Pn = n(n - 1)(n - 2)...321

Число n(n - 1)(n - 2)...*3*2*1, то есть произведение всех натуральных чисел от 1 к n, называется "n-факториалом" и обозначается n!. Отсюда Pn =n!

Пример. 5!  5 4 3 2  120 .

Un и необходимо образовать упорядоченное подмножество множества Un, которое содержит к элементов (то есть образовать размещение). Делаем это так:

Задачи на подсчет числа подмножеств конечного множества называются комбинаторными.

ЛЕКЦИЯ 2.

События и операции над ними.

Пространство элементарных исходов.

Основным понятием теории вероятностей является множество всех возможных результатов данного случайного эксперимента.

Определение . Пространством элементарных исходов называется множество  , содержащие все возможные взаимоисключающие результаты данного случайного эксперимента. Элементы множества  называются случайными исходами и обозначаются буквой w .

Любое не пустое множество  можно считать пространством элементарных исходов какого-то случайного эксперимента.

Определение. Событиями называются подмножества множества  . Говорят, что произошло событие А, если эксперимент завершился одним

из элементарных исходов, входящих в множество А.

Значит, элементарный исход – это мельчащий неделимый результат эксперимента, а событие может состоять из одного или нескольких исходов.

Напоминаю, что конечные и счетные множества можно задавать перечислением их элементов.

Например, множество  1,2,3,...,100- множество, состоящее из первых 100 натуральных чисел. Несчетные множества обычно задают указанием свойства, которым обладают все элементы множества. Например, множество

  w  R, w2  9- множество всех действительных чисел находящихся между -3 и 3.

Примеры.

1. Один раз подбрасываем игральную кость. Пространство элементарных исходов  1,2,3,4,5,6. Элементарные исходы здесь это количество выпавших очков.

Событие A 1,2 произойдет, если выпадет 1 или 2 очка.

Событие B 1,3,5 произойдет, если выпадет нечетное количество очков. Событие C 6 произойдет, если выпадет 6 очков.

2. Подбрасываем две игральные кости. Будем считать их различными и назовем одну из них первой, другую - второй. Пространством элементарных

исходов будем называть множество пар чисел i, j , где i - количество очков

выпавших на первой кости, а j - на второй кости. В этом множестве 6*6=36 элементарных исходов и все они равновозможные.

Событие А – на первой кости выпадет одно очко – записывается так

A  (1,1);(1,2);(1,3);(1,4);(1,5);(1,6)

Событие В – на второй кости выпадет два очка – записывается так

B  (1,2);(2,2);(3,2);(4,2);(5,2);(6,2)

Событие С – сумма выпавших очков равна 4- записывается так

C (1,3);(2,2);(3,1)

Операции над событиями

В теории вероятностей те же операции над событиями, как и в теории множеств. События и действия над ними иллюстрируются с помощью диаграмм Венна: достоверные события изображаются с помощью прямоугольника, элементарные случайные события – точками прямоугольника, случайное событие областью внутри него.

Определение. Объединением A  B событий А и В называется событие, состоящее в том, что произошло хотя бы одно из событий А или В.

Определение. Пересечением A  B событий А и В называется событие, состоящее в том, что произошли сразу оба события и А и В.

Определение. Дополнением А\В события В до события А называется событие, состоящее в том, что произошло А, но не произошло В.

Определение. Противоположным (или дополнительным) к событию А называется событие A   \ A , состоящее в том, что событие А не произошло.

Выделим среди подмножеств два особых события.

Определение. Достоверным называется событие, которое обязательно произойдет в результате эксперимента, т.е. единственное событие, включающее все элементарные исходы – событие  .

Определение. Невозможным называется событие, которое не может

произойти в результате эксперимента, т.е. событие не содержащее ни одного элементарного исхода – пустое множество - Ш.

Отсюда   Ш, A  A  Ш, A  A   . Объединение и пересечение событий связаны соотношениями двойственности:

A  B  A  B, A  B  A  B

Определение. События называются несовместимыми (несовместными) если наступление одного из них исключает наступление любого другого. В противном случае события называются совместимыми (совместными).

Например, получение студентом оценок 3,4,5 на одном экзамене события несовместимые, а на трех разных экзаменах совместимые.

Определение. События называются равновозможными, если в результате испытания по условиям симметрии ни одно из этих событий не является объективно более возможным.

Определение. Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти, хотя бы одно из них.

Например, событие, состоящее в том, что в семье с двумя детьми:

А – в семье два мальчика; В – в семье мальчик и девочка; С – в семье две девочки – являются единственно возможными.

Определение. Несколько событий образуют полную группу (полную систему), если они являются единственно возможными и несовместными исходами испытания.

Это означает, что в результате испытания должно произойти одно и только одно из этих событий.

Вероятностное пространство.

Случай конечного или счетного числа исходов.

Для построения полной и законченной теории случайного эксперимента теории вероятностей, кроме введенных понятий случайного эксперимента, элементарного исхода, пространство элементарных исходов, события, введем аксиому (пока еще для случая конечного или счетного пространства

элементарных исходов). Каждому элементарному исходу wi множества  отвечает некоторая неотъемлемая числовая характеристика Pi шансов его

появления - вероятность результата wi и, причем

P1 P2 .... Pn ...   Pi 1

wi 

Отсюда следует, что 0  Pi 1 для всех i .

Вероятность любого события А определяется как сумма вероятностей всех элементарных исходов, которые способствуют событию А. Обозначим ее Р(А).

Отсюда следует, что 1) 0  Pi 1

2)P( )=1;

3)P(Ш)=0.

Будем говорить, что задано вероятностное пространство, если заданное пространство элементарных исходов  и определенное соответствие

wi  P(wi )  Pi .

ЛЕКЦИЯ 3.

Классическое определение вероятности.

Вычислять вероятности P(wi ) можно, используя априорный подход, который заключается в анализе специфических условий данного эксперимента (до проведения самого эксперимента). Возможная ситуация, когда пространство элементарных событий состоит из конечного числа N элементарных событий, причем случайный эксперимент таков, что вероятности осуществления каждого из этих N элементарных событий одинаковы.

Примеры таких случайных экспериментов: подбрасывание симметричной монеты, бросания правильной игральной кости, случайное вытаскивание игральной карты из потасованной колоды.

В силу аксиомы вероятности каждого элементарного результата в этом

1

случае равняются N . Из этого следует, что если событие А содержит N A

В данном классе ситуаций вероятность события определяется как отношение числа благоприятных исходов к общему числу всех возможных исходов.

Пример. Из набора, который содержит 10 одинаковых на вид электроламп, среди которых 4 бракованих, случайным образом выбирается 5 ламп. Какая вероятность, что среди избранных ламп будут 2 бракованные?

В первую очередь отметим, что выбор любой пятерки ламп имеет одинаковую вероятность. Всего существует C105 способов составить такую

пятерку, то есть случайный эксперимент в данном случае имеет равновероятностных исходов. Сколько из этих исходов удовлетворяют условию "в пятерке две бракованных лампы", то есть сколько исходов входит в событие?

Каждую пятерку можно составить так: выбрать две бракованных лампы,

что можно сделать числом способов C42 . Каждая пара бракованных ламп может встретиться столько раз, сколькими способами ее можно дополнить тремя не

бракованными лампами, то есть C63 раз. Следовательно число пятерок, что

Статистическое определение вероятности.

Рассмотрим случайный эксперимент, который заключается в том, что подбрасывается игральная кость, сделанная из неоднородного материала. Ее центр веса не находится в геометрическом центре. В этом случае мы не можем считать последствия (выпадение единицы, двойки, и так далее) равновероятностными. Из физики известно, что кость чаще будет падать на ту грань, что ближе к центру веса. Как определить вероятность выпадения, например, трех ? Единственное, что можно сделать, это подкинуть эту кость n раз (где n-достаточно большое число, скажем n=1000 или n=5000), подсчитать

число выпадений трех n3 и считать вероятность результата, который

заключается в выпадении трех, n3 n - относительная частота выпадения трех. Аналогичным образом можно определить вероятности других

элементарных исходов — единицы, двойки, четверки, и так далее Теоретически такой образ действий можно оправдать, если ввести статистическое определение вероятности.

Вероятность P(wi ) определяется как предел относительной частоты

появления результата wi в процессе неограниченного увеличения числа случайных экспериментов n, то есть

где mn (wi ) – число случайных экспериментов (из общего числа n случайных экспериментов), в которых зарегистрированное появление

элементарного исхода wi .

Геометрическая вероятность

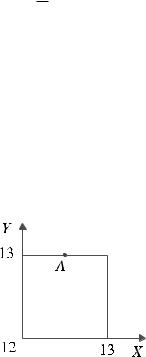
В одном специальном случае дадим определение вероятности события для случайного эксперимента с счетным множеством исходов.

Если между множеством  элементарных исходов случайного

эксперимента и множественным числом точек некоторой плоской фигуры  (сигма большая) можно установить взаимно-однозначное соответствие, а также можно установить взаимно-однозначное соответствие между множественным числом элементарных исходов, благоприятных событию А, и множественным

числом точек плоской фигуры (сигма малая), что есть частью фигуры  , то

, где s — площадь фигуры , S — площадь фигуры  . Пример. Два мужчины обедают в столовой, которая открыта с 12 до 13

часов. Каждый из них приходит в произвольный момент времени и обедает в течение 10 минут. Какая вероятность их встречи?

Пусть x — время прихода первого в столовую, а у — время прихода второго .

Можно установить взаимно-однозначное соответствие между всеми парами чисел (x;y) (множеством исходов) и множественным числом точек квадрата со стороной, ровной 1, на координатной плоскости, где начало координат отвечает числу 12 по оси X и по осе Y, как изображено на рисунке.

Здесь, например, точка А отвечает результату, который заключается в том, что первый пришел в 12.30, а второй - в 13.00. В этом случае, по-видимому, встреча не состоялась.

Если первый пришел не позже второго ( y  x ), то встреча состоится при условии 0  y x 1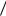6 (10 мин.- это 1/6 часы).

Если второй пришел не позже первого ( x  y ), то встреча состоится при

условии 0  x y 1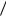6 . Между множеством исходов, благоприятных встрече, и множеством точек области , изображенной на рисунке в заштрихованном виде, можно установить взаимно-однозначное соответствие.

области можно определить как разницу единицы и суммарной площади двух

25 11

треугольников, изображенных на рисунке. Отсюда следует p  1 36  36

ЛЕКЦИЯ 4.

Непрерывное вероятностное пространство.

Как уже говорилось раньше, множество элементарных исходов может быть более, чем счетным (то есть бесчисленным). В этом случае нельзя считать любое подмножество  множества событием. Чтобы ввести определение случайного события, рассмотрим систему (конечную или счетную) подмножеств пространства элементарных исходов  .

Вслучае выполнения трех условий:

1) принадлежат этой системе;

2)из принадлежности А этой системе выплывает принадлежность A

этой системе;

3) из принадлежности Ai и Aj следует принадлежность Ai  Aj (объединение) этой системе, такая система подмножеств называется алгеброй.

Пусть  - некоторое пространство элементарных исходов. Убедимся в том, что две системы подмножеств:

Пусть A1 и A2 принадлежат некоторой алгебре.

Подмножество А несчетное множество элементарных исходов  является событием, если оно принадлежит некоторой алгебре.

Сформулируем аксиому, названную аксиомой О.М. Колмогорова.

Каждому событию отвечает неотрицательное и не больше единицы число P(А), которое имеет название вероятность события А, причем