Лекция № 4. Кривые на эллипсоиде вращения..

Вопросы лекции:

1. Взаимные нормальные сечения.

2. Геодезическая линия.

1. Взаимные нормальные сечения.

Н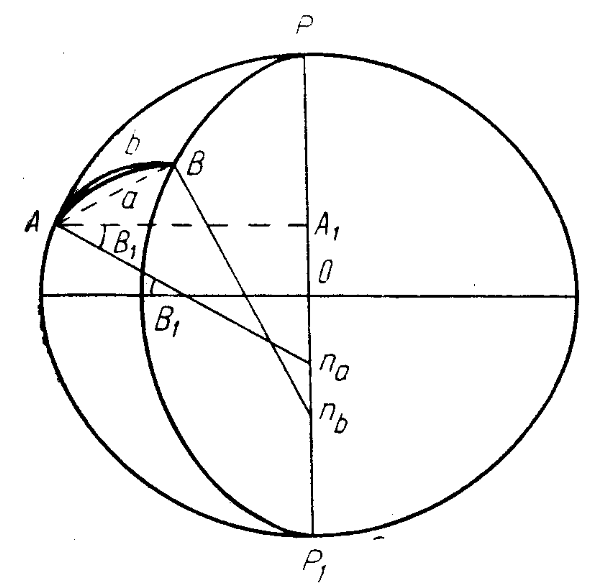ормали к поверхности эллипсоида, проведенные из двух точек с разными широтами, пересекаются с его малой полуосью в разных точках. Действительно:

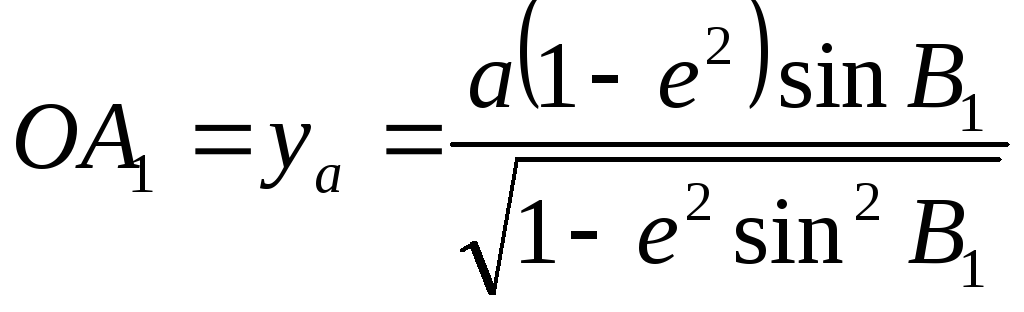
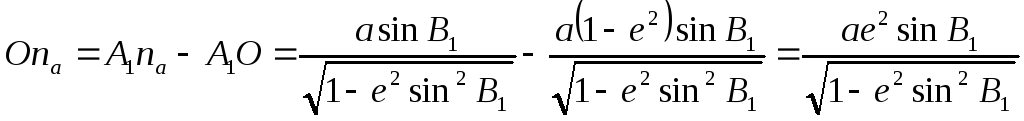
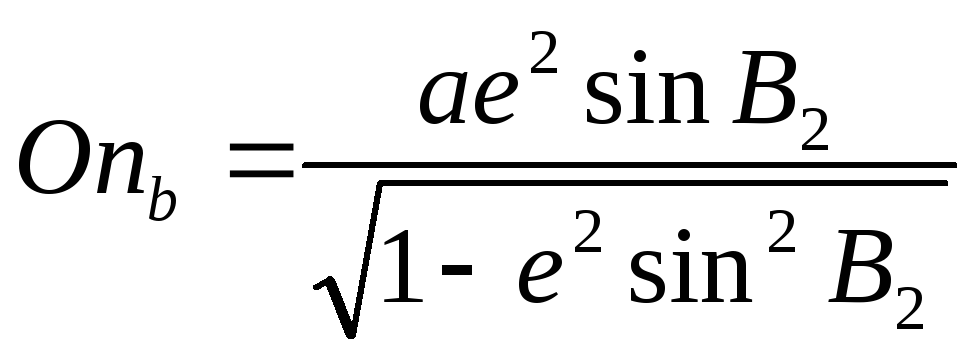
так как В₂>В₁ то On_b>On_a, т.е нормаль к поверхности эллипсоида, проведенная в точке А, имеющей меньшую широту, чем точка В, пересекает малую ось ближе к центру эллипсоида, чем нормаль, проведенная в точке В.

Таким образом , эти нормали представляют собой две перекрещивающиеся в пространстве, но не пересекающиеся прямые (если А и В не лежат на одном меридиане).

Плоскость, проведенная через точки А, n_a и В, в которой лежит нормаль Аn_a будет нормальной плоскостью в точке А, проходящей через точку В. В пересечении с поверхностью эллипсоида она даст кривую АаВ, которая называется прямым нормальным сечением в точке А на точку В.

Плоскость, проведенная через точки В, n_b и А является плоскостью нормального сечения из точки В на точку А; эта плоскость пересечётся с плоскостью нормального сечения из точки А на В по хорде АВ, но на поверхности эллипсоида даст другую кривую ВbА , не совпадающую с кривой АаВ. Таким образом нормальное сечение АаВ из точки А на точку В не совпадает на поверхности с нормальным сечением ВbА из точки В на точку А. Эти две кривые АаВ и ВbА называются взаимно обратными нормальными сечениями.

Если установить в точке А выверенный теодолит таким образом, чтобы его вертикальная ось совпала с нормалью; тогда при наведении на точку В визирная плоскость совпадёт с плоскостью проходящей через точки А, n_a, В или с плоскостью прямого нормального сечения из А на В и её пересечение с с поверхностью эллипсоида даст кривую АаВ. При наблюдении из точки В на точку А визирная плоскость теодолита пересечёт поверхность эллипсоида по кривой ВbА, не совпадающей с кривой АаВ.

Е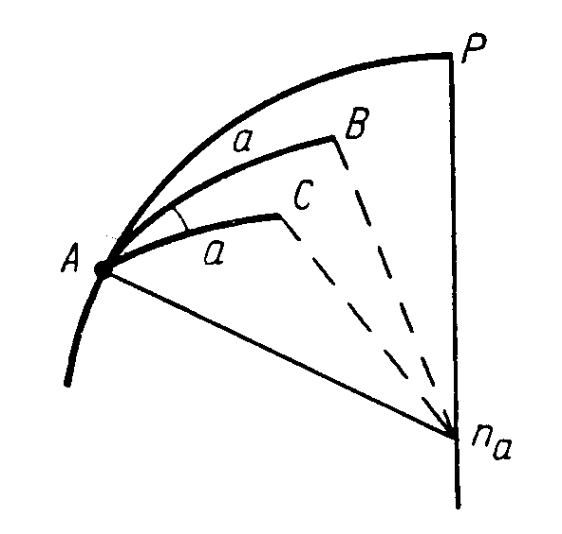сли из точки А при помощи теодолита наблюдать, кроме точки В, ещё и точку С; в этом случае визирная плоскость инструмента пересечёт поверхность эллипсоида по кривой АаС, которая будет прямым нормальным сечением из точки А на точку С. Измеренный горизонтальный угол в точке А между направлениями на В и С будет мерой двухгранного угла ВАСn_a между нормальными плоскостями в А, проходящими через точки В и С. Таким образом измеряемые в триангуляции углы треугольников на поверхности эллипсоида являются углами между прямыми нормальными сечениями в данной точки.

На следующем рисунке изображены пункты триангуляции А,В и С, между которыми проведены прямые и обратные сечения. Измеренные горизонтальные углы на пунктах А, В и С будут равны углам между касательными в соответствующих вершинах к кривым:

• в точке А к кривым АаС и АаВ,

• в точке В к кривым ВвА и ВвС,

• в точке С к кривым СсВ и СсА.

Несовпадение прямых и обратных сечений (двойственность нормальных сечений) приводят к тому, что измеренные горизонтальные углы на трёх пунктах не образуют на поверхности эллипсоида замкнутой фигуры; фигура получается «разорванной». Эту неопределённость в образовании треугольников можно устранить, если их вершины соединить геодезическими линиями.