Лекция № 5. Решение геодезических треугольников.

Вопросы лекции:

1. Виды геодезических треугольников.

2. Решение сферических треугольников по теореме Лежандра.

3. Решение сферических треугольников по способу аддитаментов.

1. Виды геодезических треугольников.

Триангуляция как основной метод построения геодезической сети на земной поверхности состоит из различного вида треугольников, вершинами которых являются геодезические пункты. Измеренные на этих пунктах угловые и линейные величины исправляются различного рода поправками, учитывающими инструментальные погрешности и влияние внешней среды.

Для математической обработки измеренных величин в триангуляции в настоящее время применяют два принципиально различающихся друг от друга метода.

В первом методе уравниваются совместно все измеренные в треугольниках величины: горизонтальные углы, зенитные расстояния и длины сторон. Триангуляционная сеть в этом случае рассматривается как пространственное построение в виде своеобразного многогранника, гранями которого являются плоские треугольники.

Во втором методе уравнивания геодезической сети все геодезические пункты проектируются на поверхность земного эллипсоида по нормалям к этой поверхности. Проекции геодезических пунктов соединяются геодезическими линиями.

Треугольники на поверхности эллипсоида, образованные геодезическими линиями, называются сфероидическими треугольниками.

Уравниванию подлежит геодезическая сеть, состоящая из сфероидических треугольников.

Для получения элементов сфероидического треугольника необходимо перейти от измеренных горизонтальных углов (или направлений) и прямолинейных сторон пространственного треугольника к соответствующим углам и сторонам сфероидического треугольника. Затем посредством решения сфероидического треугольника найти неизмеренные длины сторон.

С целью упрощения вычислений возникает необходимость замены поверхности эллипсоида более простой поверхностью шара.

Поверхность эллипсоида не развёртывается на шаре, т.е. её невозможно наложить всеми точками на поверхность шара так, чтобы расстояния между точками не изменились. На практике обычно приходится иметь дело с треугольниками, стороны которых не превышают 40÷50 км и в редких случаях достигают 70÷80 км. Вследствие близости земного эллипсоида к сфере различия в элементах сферических и сфероидических треугольников в триангуляции невелики и ими пренебрегают. При больших расстояниях учитывают возникающие искажения углов и длин линий по соответствующим формулам. Таким образом, вычисление триангуляции сводится к решению сферических треугольников, которые решаются с использованием теоремы Лежандра или способом аддидаментов.

2. Решение сферических треугольников по теореме Лежандра.

Если стороны плоского и сферического треугольников соответственно равны, то углы плоского треугольника равны углам сферического треугольника, уменьшенным на одну треть сферического избытка.

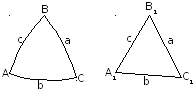
Сумма углов сферического треугольника равна:

(А+В+С) = 180º + ε

где ε – сферический избыток треугольника

Р – площадь треугольника

R – средний радиус кривизны сферического треугольника

Углы плоского треугольника определяются по формулам:

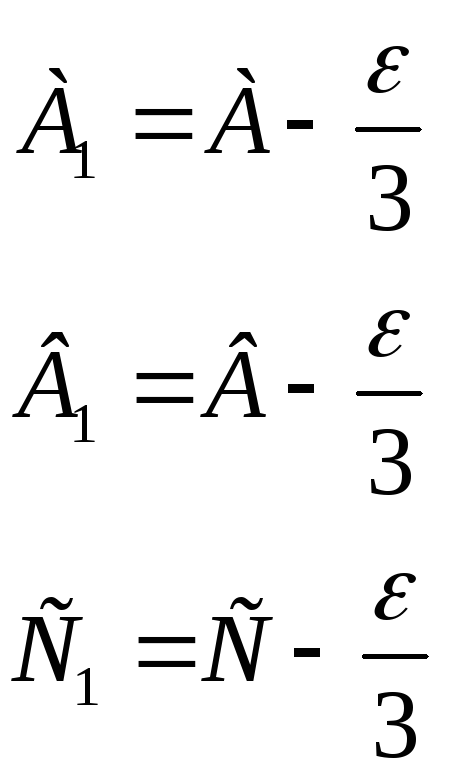
Углы А₁, В₁, С₁ называют плоскими приведенными углами.

Площадь плоского треугольника можно вычислить по формуле:

тогда:

В этих формулах сферический избыток по любым двум сторонам. Но эти формулы можно преобразовать так, чтобы сферический избыток был функцией только одной стороны. Рассматривая сферический треугольник как плоский можно записать:

А+В+С=180°

С учётом этого сферического избытка можно привести к виду:

Так как для плоского треугольника:

то:

Аналогично можно найти:

Используя эти соотношения можно вывести ещё одну группу формул сферического избытка:

Формулы:

обладают одинаковой точностью. В триангуляции 1 класса сферический избыток вычисляется с точностью до 0,001″.

Если стороны сферического треугольника меньше 90км., то при вычислении сферического избытка различием между сферическими углами и их приведенными значениями можно пренебречь.

При больших расстояниях переход к плоским приведенным углам совершается по формулам:

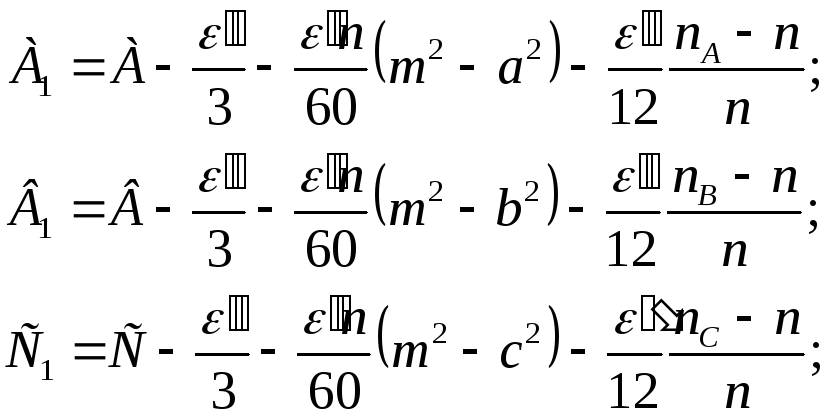
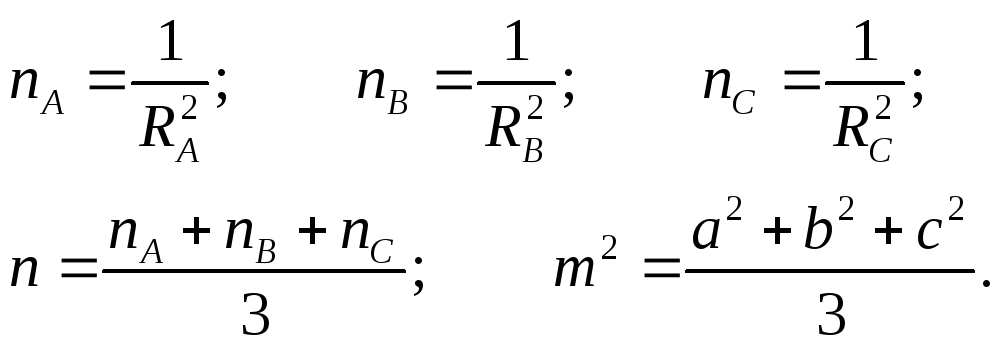
где: n_A, n_B, и n_C – Гауссова кривизна вершин треугольника АВС. Треугольники при этом рассматриваются как сфероидические. Суммарное значение поправок меньше 0,001″,если стороны треугольника не превосходят 200 км.

Более точная формула для сферического избытка имеет вид:

При вычислении сферического избытка поправочный член следует учитывать, если стороны треугольника больше 90 км.

Если стороны треугольника близки или больше 90 км, сферический избыток следует вычислять двумя приближениями: сначала получить приближённое значение сферического избытка по формуле: и по нему вычислить приближённое значение приведенного плоского угла . С этим приближенным значением угла сферический избыток вычисляется по формуле

Порядок вычислений при решении сферических треугольников по трём углам и одной стороне:

1. Вычисляется сферический избыток треугольника.

2. От углов сферического треугольника переходят к приведенным значениям углов плоского

3. Решая треугольник как плоский, по исходной стороне вычисляют его искомые стороны.

Решение сферического треугольника по трём сторонам.

При использовании теоремы Лежандра по трём сторонам треугольники следует решать как плоские, принимая стороны сферических треугольников прямолинейными, а к вычисленным таким образом углам треугольников прибавлять поправки равные .

В этом случае формулы для вычислений углов плоского треугольника будут иметь вид:

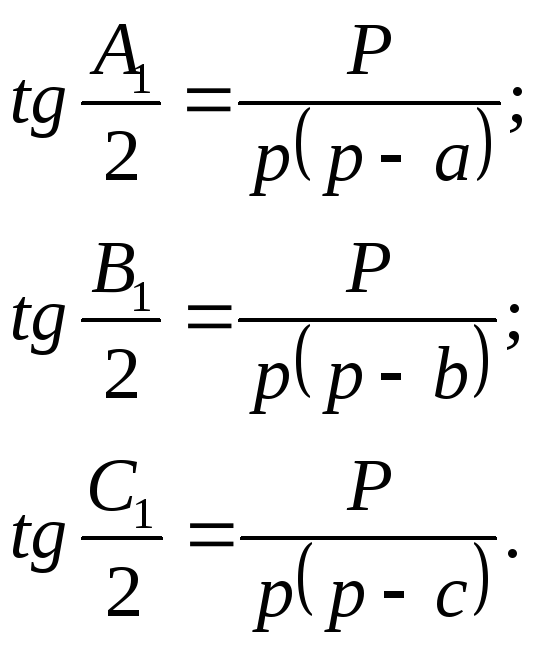
где Р – площадь, а р – полупериметр треугольника АВС:

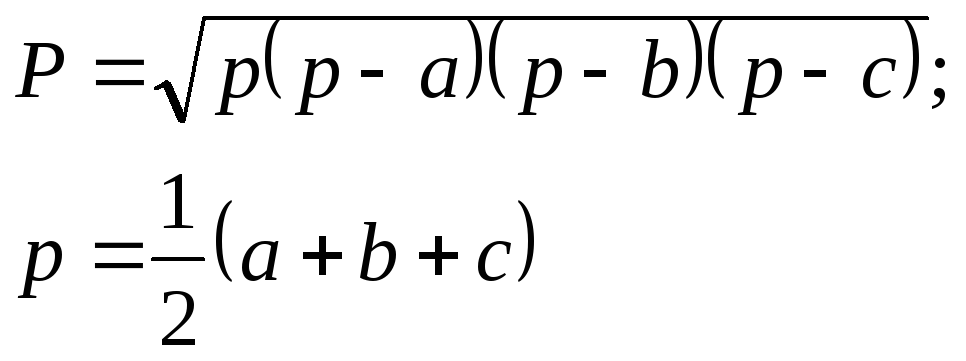
Углы сферического треугольника вычисляются по формулам:

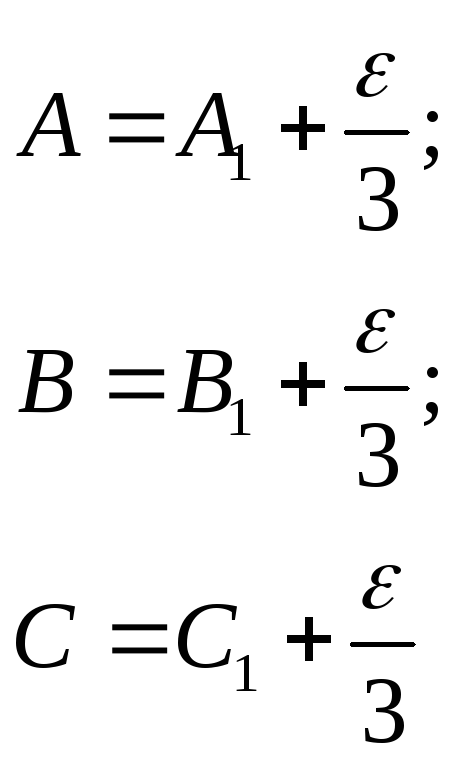
Формула для вычисления сферического избытка:

Порядок вычислений при решении сферических треугольников по трём сторонам:

4. Вычисляется полупериметр и площадь сферического треугольника.

5. Решая треугольник как плоский, вычисляют приведенные значения углов треугольника.

6. Вычисляется сферический избыток треугольника.

7. От приведенных значений углов плоского треугольника переходят к углам сферического треугольника.