Входные данные по индивидуальному варианту
Таблица 1 – Входные данные
|
№ варианта |
Вариант данных файла данных |
Варианты данных на входе модели (из файла данных) |
Варианты данных на выходе модели (из файла данных) |
Вариант к заданию 1 |
Вариант стат. модели (задание 2.1) |
Вид динам. моделей (задание 3.4) |
Динам. характеристики (задание 3.5) |
|
7 |
1 |
х1, х3, х4, х5 |
y3 |
a), f), h) |
g) |
ARMAX, BJ |
c) |
Задание 1. Анализ статистических характеристик объекта по данным пассивного эксперимента и выбор структуры модели
Определить среднее, медиану, дисперсию, среднеквадратическое отклонение на всех параметров на входе и выходе.
load C:\Users\Devil\Desktop\kurs\dan1.txt
x1=dan1(:,2); x2=dan1(:,4); x3=dan1(:,5); x4=dan1(:,6); y=dan1(:,12);
Среднее значение
>> mean(x1) ans = 87.0833
>> mean(x2) ans = 68.1500
>> mean(x3) ans = 59.9333
>> mean(x4) ans = 0.2833
>> mean(y) ans = 20.8167
Среднеквадратическое отклонение
>> std(x1) ans = 1.4531
>> std(x2) ans =1.1619
>> std(x3) ans =3.0077
>> std(x4) ans = 1.5081
>> std(y) ans = 0.9828
Дисперсия
>> sqrt(std(x1)) ans =1.2055
>> sqrt(std(x2)) ans =1.0779
>> sqrt(std(x3)) ans =1.7343
>> sqrt(std(x4)) ans =1.2280
>> sqrt(std(y)) ans =0.9913
Построить графики и гистограммы каждого параметра.
Графики
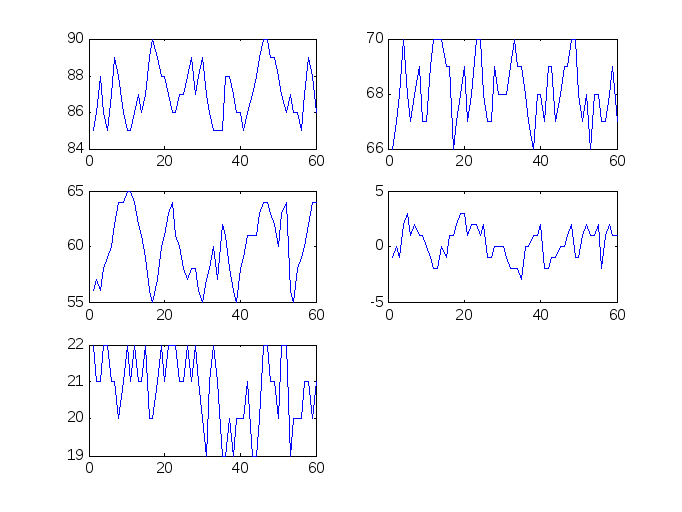
subplot(3,2,1),plot(x1)
subplot(3,2,2),plot(x2)
subplot(3,2,3),plot(x3)
subplot(3,2,4),plot(x4)
subplot(3,2,5),plot(y)
Рис. 1 – Графики параметров объекта на входе и выходе
Гистограммы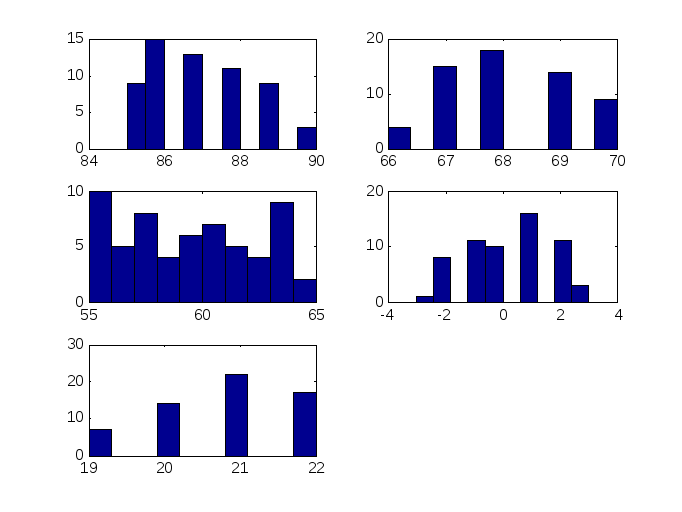
>> subplot(3,2,1),hist(x1)
>> subplot(3,2,2),hist(x2)
>> subplot(3,2,3),hist(x3)
>> subplot(3,2,4),hist(x4)
>> subplot(3,2,5),hist(y)
Рис. 2 – Гистограммы параметров объекта на входе и выходе
Вычислить матрицу коэффициентов корреляции параметров
>> z=[x1 x2 x3 x4 y];
>> corrcoef(z)
ans =
1.0000 -0.0176 -0.0103 0.2520 -0.1078
-0.0176 1.0000 0.3182 -0.1214 0.2323
-0.0103 0.3182 1.0000 0.0453 0.2940
0.2520 -0.1214 0.0453 1.0000 0.1843
-0.1078 0.2323 0.2940 0.1843 1.0000
1.4.a. Оценить стационарность данных за критерием серий.
function seria(x,n)
medx=median(x);
v=x-medx;
s=1;
for i=2:n
if (v(i).* v(i-1)<0)
s=s+1;
end;end;
if ((s>24) & (s<37))
disp ('стационарен за критерием серий')
else
disp ('не стационарен за критерием серий')
end;
>> seria(x1,60)
не стационарен за критерием серий
>> seria(x2,60)
не стационарен за критерием серий
>> seria(x3,60)
не стационарен за критерием серий
>> seria(x4,60)
не стационарен за критерием серий
>> seria(y,60)
не стационарен за критерием серий
Вывод: Оценив стационарность данных по критерию серий Вальда –Вольфовица, определил, что все входные и выходные параметры не стационарны.
1.4.f. Оценить нормальность закона распределения за критерием Колмогорова
function kal(x,n)
k=fix(1+3.31+log10(n));
mx=mean(x);
s=std(x);
f=hist(x,k);
p=f./n;
ff=zeros(1,k+1);
for i=1:k
ff(i+1)=f(i).*p(i);
end;
dx=max(x)-min(x)./k;
for i=1:k+1
xk(i)=min(x)+(i-1).*dx;
end;
sx=(xk-mx)./s;
for i=1:k+1
f(i)=quad('exp(-t.^2)/2',0,sx(i));
end;
ft=0.5+f(i)./sqrt(2.*pi);
Kn=max(abs(ft-ff).*sqrt(n))
if(Kn<1.35)
disp('нормальный закон распределения')
else
disp('не нормальный закон распределения')
end;
>> kal(x1,60) Kn = 23.8051 не нормальный закон распределения
>> kal(x2,60) Kn =36.5859 не нормальный закон распределения
>> kal(x3,60) Kn =16.5755 не нормальный закон распределения
>> kal(x4,60) Kn =27.8072 не нормальный закон распределения
>> kal(y,60) Kn =57.2418 не нормальный закон распределения
Вывод: Оценив нормальность закона распределения за критерием Колмогорова, определил, что все параметры распределены не по нормальному закону распределения.
1.4.h. Определить оптимальный шаг квантования и длину реализации экспериментальных данных
MY=[x1 x2 x3 x4 y];
tmax(MY,60,4)
function [tmax,delta]=tmax(MX,n,m)
tmax=zeros(m+1,1);
zk=[MX(:,1) MX(:,m+1)];
R=covf(zk,n-1);
Ryy=R(1,:);
plot(Ryy)
tmax(1)=0;
for i=1:n-1
if abs(Ryy(i)>=0.05*Ryy(1))
tmax=i;
end;end;
for k=1:m
zk=[MX(:,1) MX(:,m+1)];
R=covf(zk,n-1);
Rxx=R(1,:);
tmax(k+1)=0;
for i=1,n-1
if (abs(Rxx(i)>=0.05*Rxx(1)))
tmax(k+1)=i;
end;end;end;
tomax=max(tmax);
tomin=min(tmax);
treal=tomax*16;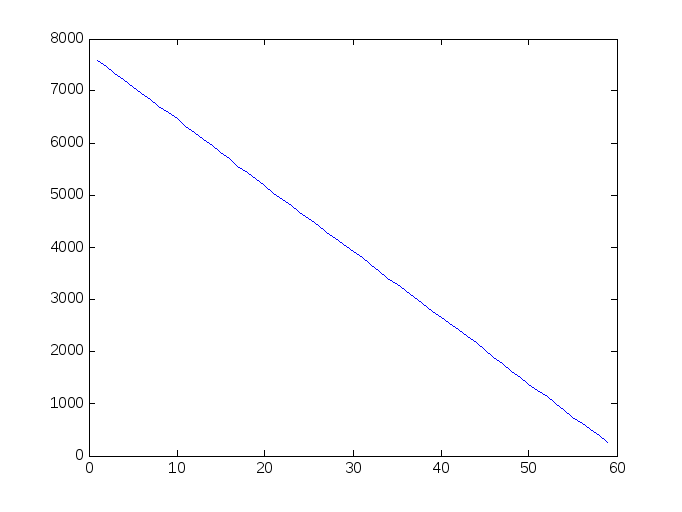
delta=tomin/10;
treal
delta
tmax(MY,60,4)
treal =912
delta = 0.1000
ans = 57 1 1 1 1
Рис.3 График ковариационной матрицы
Вывод: Определил оптимальный шаг квантования и длину реализации экспериментальных данных. Время реализации 0,1с., шаг квантования 912.