Рух центра маси механічної системи

Для системи, яка складається з матеріальних точок, положення центра маси механічної системи (радіус-вектор ) визначається виразом

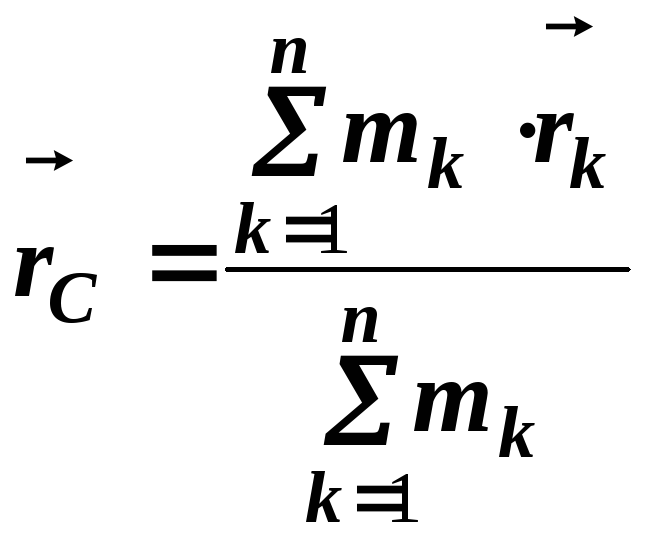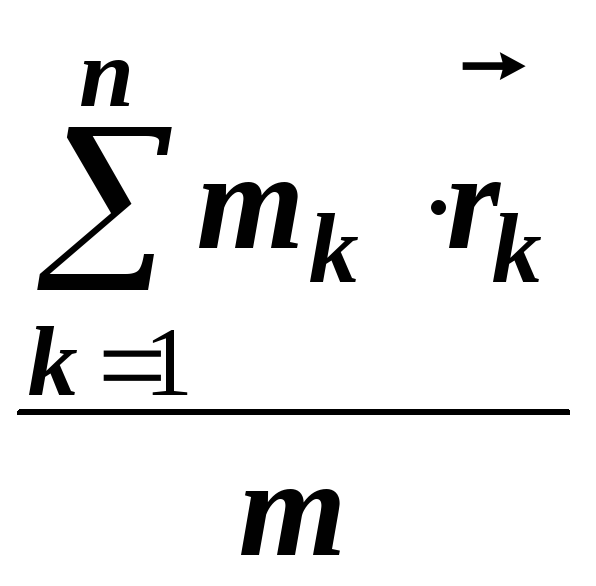= , (1)

де – радіус-вектори матеріальних точок, що входять до системи.

Виходячи з визначення головного вектора зовнішніх сил, можна показати, що центр маси механічної системи рухається як вільна матеріальна точка, маса якої дорівнює сумі мас всіх елементів системи () і на яку діє сила, що дорівнює головному вектору зовнішніх сил

= . (2)

Остання формула є математичним записом теореми про рух центра маси механічної системи, в якому – прискорення центра маси.

Векторне рівняння (1.2) еквівалентне трьом скалярним:

, , , (3)

в яких , та – компоненти вектора швидкості центра маси, а , та – координати центра маси.

З наведеної теореми випливають наступні наслідки:

1) внутрішні сили не змінюють характер руху центру маси системи;

2) якщо головний вектор зовнішніх сил дорівнює нулю, то центр маси системи рухається рівномірно та прямолінійно, або знаходиться в стані спокою, тобто

, (4)

де – початкова швидкість центра маси. Якщо = 0, то

, (5)

тобто центр маси системи не змінює свого положення в просторі;

3) якщо проекція головного вектора зовнішніх сил на деяку нерухому вісь (наприклад, ) дорівнює нулю, то проекція швидкості центра маси системи на цю вісь не змінюється(), і якщо = 0, то

, (6)

тобто центр маси системи не змінює свого положення відносно осі .

Методика розв’язання задач

1) Визначити тіла, що входять до механічної системи.

2) Визначити зовнішні сили, що діють на систему.

3) Якщо всі зовнішні сили паралельні, обрати систему координат і одну з осей (наприклад, ) спрямувати перпендикулярно до лінії їхньої дії. В проекції на цю вісь диференціальне рівняння руху центра маси приймає вигляд

= 0, (7)

де – координата центра маси.

4) Двічі інтегруючі (1.7) за умовою, що у початковий момент часу центр маси системи знаходився в стані спокою, знаходимо що

= = const. (8)

5) Рівняння (1.8) еквівалентно рівнянню

,

звідки отримуємо

= 0, (9)

в якому – абсолютні зміщення елементів системи. Ці зміщення можуть бути знайдені як алгебраїчні суми абсолютного зміщення одного з тіл (основного) та зміщень інших тіл відносно нього. З рівняння (9) визначаємо –абсолютне зміщення основного тіла.

6) Якщо зовнішні сили діють з рівнодійною вздовж осі , то теорема про рух центра маси дає

= = , (10)

де – абсолютне прискорення кожного тіла. Беремо другі похідні від абсолютних зміщень кожного тіла за умовою, що = 0 і отриманий вираз (1.10) визначає силу .

Приклад 1. Призма 3 (рис. 1) масою = 12 кг з закріпленим на ньому електродвигуном ( = 5 кг) та блоком ( = 1 кг) може ковзати вздовж горизонтальної поверхні без тертя. Два вантажі, маси яких = 4 кг та = 3 кг можуть ковзати по гладким поверхням призми, які утворюють кути = 45º та = 60º з горизонтом, бо з’єднані мотузками з двигуном та блоком . Електродвигун (радіуси шківів якого = 15 см та = 5 см), зв’язаний з блоком (радіуси шківів якого = 20 см та = 10 см), неперехресною пасовою передачею. В момент часу = 0 вал електродвигуна починає обертатися за законом рад. Знайти:

1. Закон зміщення призми від часу.

2. Реакцію упорів, які утримують призму в закріпленому стані.

3. Обчислити зміщення призми і реакцію упору на момент часу = 1 с.

Додатному напряму обертання відповідає обертання валу двигуна проти руху стрілки годинника. Вагою мотузок та пасу нехтувати і вважати їх нерозтяжними.

Розв’язання. В даному випадку механічна система складається з п’яти елементів. Зовнішніми силами є сили тяжіння, а також нормальна реакція горизонтальної площини, які спрямовані вертикально. Введемо декартову систему відліку (дивись рис.1), спрямувавши вісь горизонтально. Тоді сума проекцій усіх зовнішніх сил на вісь дорівнює нулю і, згідно з теоремою про рух центра маси механічної системи, з урахуванням того, що в початковий момент часу система знаходиться у стані спокою, маємо

= 0, (1)

де – абсолютні зміщення елементів системи вздовж осі .

Абсолютні зміщення тіл 1, 2, та знайдемо як алгебраїчну суму їхніх зміщень відносно призми та абсолютного зміщення призми = відносно нерухомої системи координат. Будемо вважати, що призма змістилася праворуч від початкового положення (рис.2). Електродвигун та блок не зміщуються відносно призми, тому

= = = . (2)

Для визначення зміщень першого та другого тіла відносно призми, треба визначити на який кут повернувся вал двигуна протягом часу і в якому напрямі відбулися відповідні лінійні зміщення тіл 1 і 2.

Додатнім напрямом обертання валу двигуна ми вважаємо його обертання в напрямі проти руху стрілки годинника (рис. 1.4). В такому випадку тіло 1 рухається ліворуч вниз. З врахуванням передачі між електродвигуном А та блоком , останній обертається також проти напряму руху стрілки годинника і тіло 2 рухається по похилій площині догори ліворуч. Модуль відносного зміщення тіла 1 вздовж похилої площини знайдемо як

= ,

тоді абсолютне зміщення першого тіла вздовж осі визначиться як

= – . (3)

Блок за той самий проміжок часу повернеться на кут проти руху стрілки годинника, який ми знайдемо за умовами нерозтяжності пасової передачі та відсутності ковзання між блоками та пасом

= ,

звідки знайдемо кут повороту блока

.

Це дає можливість визначити модуль відносного зміщення тіла 2 вздовж похилої площини

= ,

та знайти абсолютне зміщення другого тіла вздовж осі

= – . (4)

Підставимо (2), (3), (4) в (1) і отримаємо

= 0.

Якщо розкрити дужки та провести алгебраїчні перетворення, то дістанемо

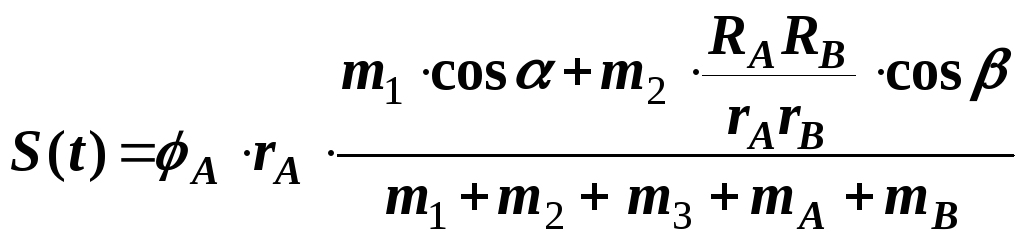. (5)

Отриманий вираз дає зміщення тіла 3 в будь-який момент часу. Підставляючи умови задачі в формулу (5) на момент часу = 1 с отримуємо

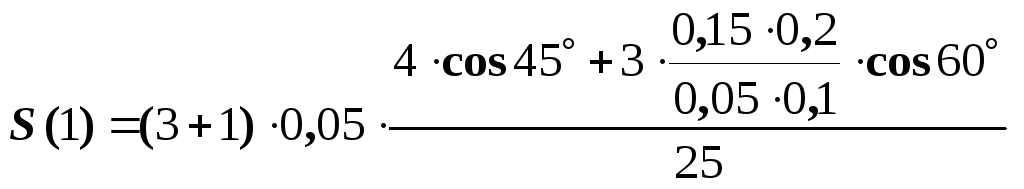= 0,09 (м).

Для відповіді на друге запитання перепишемо закон руху центра маси механічної системи у вигляді, який визначає реакцію упору

, (6)

При наявності упорів тіло 3 не рухається, отже

= = 0. (7)

Візьмемо другі похідні від (3) та (4) і, з урахуванням (7), для реакції упору отримаємо

=

= =

= . (8)

Знайдемо другу похідну по часу від :

, (рад/с²),

і, підставляючи в (8) дані задачі на моменту часу = 1 с, знайдемо

= – 1,2 (Н).

Відповідь: м, (1) = 0,09 м, = , (1) = – 1,2 Н.