4.2 Послідовний коливальний контур

Розрахункова схема послідовного навантаженого контура наведена на рис. 4.9.

а) б)

а) розгалужений, б) нерозгалужений

Рисунок 4.9 – Послідовний навантажений коливальний контур

Вихідні дані: V_m=110 B; L=0.3*10^-3 Гн; R=60 Ом; C=0.25*10^-9 Ф; R_H=60 кОм.

4.2.1 Визначаємо кутову резонансну частоту ω_p та хвильовий опір ρ:

ω_p=,

де L, C – еквівалентні індуктивність і ємність контура

С_ЕКВ= 0,5С+0,5С=С

(кОм)

4.2.2 Добротність ненавантаженого Q та навантаженого опором R_H контура:

де внесений опір R_ВH:

(Ом)

4.2.3 Розрахунок межових частот та смуги пропускання для навантаженого і ненавантаженого контура.

Верхня і нижня частоти смуги пропускання ненавантаженого контура:

де затухання контура d дорівнює:

Відносна смуга пропускання:

Для навантаженого контура смуга пропускання збільшиться:

Верхня і нижня межові частоти смуги пропускання навантаженого контура:

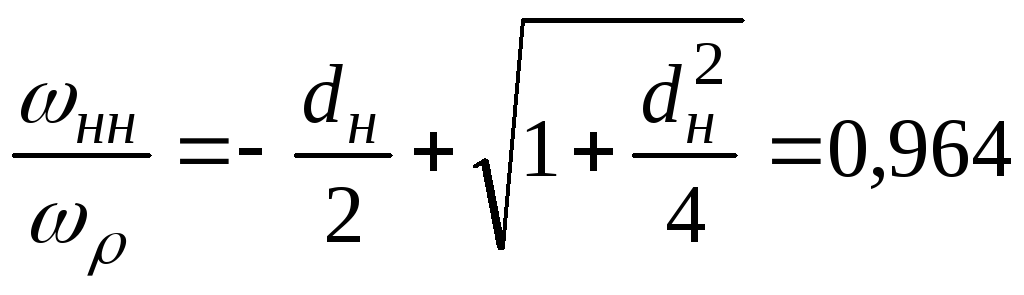
4.2.4 Комплексний вхідний опір для ненавантаженого і навантаженого контура.

При резонансі :

(Ом)

На границях смуги пропускання коливального контура активні та реактивні опори рівні за величиною . Відповідно і фазовий зсувміж напругою на затискачах кола та струмом складає

- де - узагальнене розстроюванням контуру

,

де .

Для навантаженого контуру:

Комплексний опір для межових частот:

де

4.2.5 Визначаємо комплексним методом струм і напругу на всіх ділянках навантаженого контуру для верхньої частоти, при умові

За законом Ома: при

На верхній межовій частоті , тоді початкова фаза напруги мережі теж буде дорівнювати, тобто

Комплексна амплітуда струму:

Комплексна напруга (рис. 4.9) :

(В), де

Струм у навантаженні:

Струм в ємності (рис. 4.9):

Комплексна напруга на ділянці bd:

Комплексна напруга на індуктивності:

4.2.6 Миттєві значення струмів та напруг, знайдені в п. 4.2.5:

;

;

;

;

;

;

4.2.7 Векторна діаграма напруг та струмів для верхньої межової частоти навантаженого контура подана на рис. 4.10.

Обираємо масштаби напруг та струмів:

Рисунок 4.10 – Векторна діаграма напруг та струмів.

4.2.8 Побудова резонансної кривої струму (АЧХ) I/I_P:

Модуль струму I дорівнює:

де - узагальнене розстроюванням контура

Розділивши знайдений струм на значення струму при резонансі:

отримуємо нормовану величину струму:

При малих розстроюваннях контура:

Розрахункові дані для побудови АЧХ і ФЧХ навантаженого і ненавантаженого коливального контурів наведені в таблиці 4.2.

Таблиця 4.2 – Розрахункові дані для побудови АЧХ і ФЧХ.

							град	град
0,8	-0,2	-7,3	-5,48	54,3	0,135	0,18	-82,2	-79,7
0,85	-0,15	-5,48	-4,1	31	0,18	0,24	-79,7	-76,3
0,9	-0,1	-3,65	-2,73	14,3	0,26	0,34	-74,7	-69,9

Продовження таблиці 4.2

							град	град
0,95	-0,05	-1,88	-1,36	4,3	0,48	0,59	-61,2	-53,7
	0	0	0	1	1	1	0	0
1,05	0,05	1,82	1,36	4,3	0,48	0,59	61,2	53,7
1,1 p	0,1	3,65	2,73	14,3	0,26	0,34	74,7	69,9
1,15	0,15	5,48	4,1	31	0,18	0,24	79,7	76,3
1,2	0,2	7,3	5,48	54,3	0,135	0,18	82,2	79,7

Для побудови фазочастотної характеристики (ФЧХ) скористуємося узагальненим розстроюванням контура :

Фазовий кут:

Розрахункові дані наведені в таблиці 4.2.

За результатами розрахунків на рис. 4.10 побудована АЧХ, а на рис. 4.11 побудована ФЧХ.

Рисунок 4.11 – Амплітудно-частотна характеристика: 1 – для ненавантаженого контура; 2 – для навантаженого.

Рис. 4.12 – Фазочастотна характеристика: 1 – для ненавантаженого контура; а 2 – для навантаженого.