Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Волгоградский государственный медицинский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Anisimov_Tretyakova.pdf

Скачиваний:

598

Добавлен:

09.02.2016

Размер:

3.59 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 178 9 10 11 12 13 14 15 16 17 > Следующая >>>

ψ(x) = A e−ikx ,

(2.15)

где k =	2m		(E −U (x)) .
	h	2
	h

Это решение прямого физического смысла не имеет. Следует иметь ввиду, что волновая функция должна удовлетворять стандартным условиям: однозначность, конечность, непрерывность вместе с первой производной. Она удовлетворяет условию нормировки.

∫−∞∞	ψ(x)	2dx =1	(2.16)

Если выполнить интегрирование по всем возможным местоположениям частицы, то вероятность превратится в вероятность достоверного события, поэтому волновая функция нормирована на единицу.

Подынтегральное выражение имеет физический смысл. Это плотность вероятности стационарного состояния, которая равна

w(x) =		ψ(x)		2 = ψ(x)ψ* (x),	(2.17)

где ψ*(x) - комплексно сопряженное значение ψ-функции. Для

одномерного случая вероятность обнаружить частицу в интервале [x; x+dx] определяется формулой

dW = w(x)dx (2.18)

Для одномерного случая вероятность обнаружить частицу в интервале [a; b] определяется формулой

b
W ([a;b]) = ∫\| ψ(x) \|2 dx.	(2.19)

Средние значения физических величин

Если известна волновая функция, описывающая состояние частицы в определенный момент времени, то среднее значение (математическое ожидание) физической величина А, характеризующее поведение частицы, выражается формулой

A = ∫ψ*A ψ dV.	(2.20)
V

Для одномерного случая, если х меняется от 0 до l.

l
A = ∫ψ*A ψ dx.	(2.21)
0

Например, среднее значение координаты х микрочастицы

x = ∫x ψ2dx .

Аналогично, среднее значение х3

x3 = ∫x3 ψ2dx .

2.2.Примеры решения задач

Задача 2.1. Найти длину волны де Бройля для 1) электрона, летящего со скоростью v = 106 м/с; 2) α-частицей, движущейся со скоростью, равной наиболее вероятной скорости при температуре 0°С (273 К); 3) шарика массой 106 кг, движущегося со скоростью 1 м/с? В каком из этих случаев необходимо учитывать волновые свойства частиц?

Решение. Для определения длины волны воспользуемся формулой де Бройля. λ = hp

1.Оценим λe для электрона.

			6,62 10	−34	= 7,3 10−10	o
λ	e	=				м = 7,3А.
			9,1 10−31 106

2. Определим λα для α-частицы (ядра атома гелия, 4 нуклона mα = 4 1,67 10−27 кг)

λα = mαhvнв

найдем из формулы для наиболее вероятной скорости скорость

движения α-частицы: vнв =

2RT

2kT

mα

Подставив это значение, найдем

λα =

6,62 10−34

= 0,93Å.

2mαT

1,38

10−23

1,67 10−27 2,73 102

3. Для шарика массой 10-3 кг

6,62 10−34

−21

λш =

= 6,62

Å.

10−3

Волновые свойства частиц можно обнаружить в опытах по дифракции. Явление дифракции наблюдается, если длина волны

соизмерима с размерами препятствия. Обнаружить дифракцию для волн, связанных с движением шарика невозможно, так как шарик является макроскопическим объектом и его движение описывается законами классической механики.

Задача 2.2. Доказать, что скорость движения нерелятивистских микрочастиц v равна групповой скорости vгр волн де Бройля.

Решение. Групповая скорость волн

v =

dω

d(hω)

гр

dk d(hk ) dp

Поскольку E = p2 2m ,то

d (p2 2m)

2pdp

= v = v .

2mdp

гр

Задача 2.3. Используя понятие волны де Бройля применительно к электрону в атоме водорода, вывести постулат Бора о квантовании момента импульса электрона.

Решение. Покажем, что в стационарной боровской орбите укладывается целое число длин волн де Бройля

n = 2λπr , λ = mvh .

Поэтому

n = 2πr mv , отсюда mvr = nh = nh. h 2π

Что и требовалось доказать.

Задача 2.4. Во время наблюдения дифракции электронов при рассеянии их от кристалла (опыты Девиссона и Джермера) угол скольжения электронного пучка θ = 30°. Постоянная кристаллической решетки d = 3 Å. Пренебрегая преломлением электронных волн определить энергию электронов при которых наблюдаются два первых максимума отражения.

Решение. Угловое положение максимумов при дифракции электронов (как и рентгеновских лучей) определяется с помощью формулы Вульфа-Бреггов

2d sinθ = nλ.

Считая длиной волны де Бройля, λ = h m0v = h p, получим

2d sinθ = nhp . Отсюда p = 2dnhsinθ .

Кинетическая энергия нерелятивистского электрона связана с его импульсом соотношением

W =			p2	=	n2h2	.
	2m				8d 2m sin2 θ

	0				0
Принимая n1= 1, n2 = 2, находим энергию
W1 =					12 (6,62 10−34 )2		=16,7эВ.
		8(3 10−10 )2 9,1 10−312,5 10−1 1,6 10−19
W2 =					22 (6,62 10−34 )2		= 66,9эВ.
			8(3 10−10 )2 9,1 10−312,5 10−1 1,6 10−19

Задача 2.5. Определить длину волны де Бройля для движущегося электрона, если известно, что масса m его на 1% больше массы покоя m0.

Решение.			Электрон	релятивистский,			следовательно,
m = m0		= m + 0,01m =1,01m . Так как			λ =	h	, то находим
e	v2	0	0	0	c	m2	− m2
	v2				c	m2	− m2
1− c2							0
							0
скорость	электрона		v = с 1−(m m)2 = 4,2 107			м/с.,	а длина волны
			e	0

электрона равна λ = 1,7 10-11 м = 0,17 Å.

Задача 2.6. Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью, ширина которой b = 0,1 мм. Определить скорость электрона, если известно, что на экране, отстоящем от щели на расстоянии l = 50см, ширина центрального дифракционного максимума x =80мкм.

Решение. Так как электроны обладают волновыми свойствами, воспользуемся формулой для дифракции на щели. Согласно условию

задачи	электроны,				A
попадающие	на	первый

дифракционный максимум,					B
отклоняются	в	пределах b				x
угла ϕ (рис 2.2).
Его	границы		–	l
минимумы		первого

порядка.	Линейное			Рис. 2.2.
расстояние между		ними	-
x . Условие минимума при дифракции от щели bsinϕ= kλ. Из						ОАВ

найдем tgϕ = x2l ≈sinϕ ≈ ϕ, так как ϕ мал. Следовательно, при k = 1

2xl = λb = mvbh , так как λ = mvh . Отсюда получим

v =	2hl				2 6,62 10−34 0,5				6
			=							=9 10 м/с.
	xmb			8	−5		−31	10	−4
					10	9,1 10
Задача		2.7.			Найти		неопределенность координаты				x : 1) для
электрона с энергией 1							эВ и скоростью v = 6 107 см/с,				найденной с

точностью 10%; 2) для маленькой капли массой m =5 10−7 г, диаметром

d = 0,1мм, движущийся со скоростью v =10−2 см/с, измеренной с точностью 10%.

Решение. Электрон с энергией 1 эВ нерелятивистский.

Неопределенность	скорости	электрона	vx = 6 104 м/c.
Неопределенность координаты электрона

x ≈

6,62 10−34

−7

= 0,019 10

м=19A.

m v

6,28 9,1 10

−31

Это значительно больше размеров атома (1 Å).

vx =10−5м/c.

Неопределенность

скорости

капли

Неопределенность координаты капли

x ≈

6,62 10−34

−20

−10

= 2,1 10

м= 2,1 10

m vx

6,28

−10

−5

5 10

Это во много раз меньше диаметра капли.

Задача 2.8. Оценить неопределенность в угловой координате ϕ момента импульса электрона L в атоме водорода.

Решение. В соответствии с постулатом Бора момент импульса электрона в атоме водорода квантуется L = mvr = nh. Момент импульса

L и угловая координата ϕ – сопряженные физические величины.

Соотношение неопределенности для них имеет						вид	L ϕ≥h. Для
оценки в случае, если	L = L то ϕ≈	h	=	h	=	1 .	Для основного
		L		nh
						n

состояния атома водорода n = 1, тогда ϕ =1рад=57,3°. Это значит,

что говорить об определенной траектории электрона в невозбужденном атоме водорода нельзя.

Задача 2.9. Кинетическая энергия электрона в атоме водорода Т = 10эВ. Используя соотношение неопределенности, оценить минимальные размера атома.

Решение. Неопределенности координаты и импульса связаны соотношением r p ≥ h. Если атом имеет линейный размер l, то можно

считать			r = l 2.	Неопределенность импульса не должна превышать
самого		импульса.		Тогда l ≥ 2h p .		Импульс связан с кинетической
энергией соотношением p = 2mT . Следовательно,
l	=	2h	=	2 6,62 10	−34	=1,24 10−10	o
							м =1,24A.
	min	2mT 6,28		2 9,1 10−31 10 1,6 10−19

Задача 2.10. Используя соотношение неопределенности, оценить ширину энергетического уровня в атоме водорода, находящемся: 1) в

возбужденном состоянии, где время жизни τ =10−8с; 2) в основном состоянии, где время жизни τ = ∞.

Решение. Неопределенность времени жизни не должна

превышать

самого

времени

жизни,

τ = τ.

Из соотношения

неопределенности E τ≥ h получим для оценки

Eτ ≈ h. Здесь

E -

ширина энергетического уровня или энергетическая зона.

Если τ =10−8с, то

E ≈

1,05 10−34

−26

−8

10−8

=1,05 10

Дж

= 7 10

эВ.

U(x)

Если, τ = ∞, то

E = 0.

Задача 2.11. Частица находится в

III

одномерной

прямоугольной

потенциальной

яме с бесконечно высокими стенками и

шириной

(Рис.2.3). Найти

возможные

значения

энергии,

выражения

для

собственных

функций

частицы

распределение

вероятности

обнаружения

Рис. 2.3.

частицы по ширине ямы.

Решение. По условию задачи

U(x) = 0 при 0 < x < l; U(x) = ∞ при x ≤ 0, x ≥ l.

Все пространство -∞ < х < ∞ разобьем на три области: I, II, III. Поскольку потенциальная яма имеет бесконечно высокие стенки, то электрон не может выйти за ее пределы, т.е. вероятность обнаружить электрон в областях I и III равна нулю: |ψ1(x)|2 = 0 и |ψ3(x)|2 = 0.

Граничные условия непрерывности волновой функции ψ в точках x1 = 0 и x2 = l имеют вид

ψ1(0) = ψ2(0) = 0; ψ2(l) = ψ3(l) = 0.

Запишем уравнение Шредингера для электрона в области II

d 2ψ2 + 2m Eψ2 = 0. dx2 h2

Здесь

k2 = 2hmE2 .

С учетом введенного обозначения уравнение Шредингера запишем в виде

d 2ψ22 + k2ψ2 = 0.

Его решение будем искать в виде

ψ2(x) = Asin(kх) + Вcos(kх),

где A и B - некоторые постоянные, определяемые из граничных условий. Используя граничные условия при x = 0 получим, что константа B = 0. Подставляя x = l, находим ψ2(l) = 0, то есть Asin(kl) = 0. Поскольку A ≠ 0, то sin(kl) = 0. Тогда

k l = nπ,

где n = 1,2,3… Откуда находим возможные значения энергии электрона

Еn = π2h2 n2.

2ml2

Таким образом, граничные условия выполняются лишь для дискретного ряда значений энергии En. Следовательно, из решения уравнения Шредингера следует, что частица, находящаяся в потенциальной яме, может иметь только дискретный спектр энергий.

Теперь решение уравнения Шредингера можно записать в виде ψ2(x) = Asin(kl), или подставив значения k = nπ/l, получим

ψ2 (х) = Аsin(

nπ

х).

Постоянную A найдём из условия нормировки на единицу:

∫l

ψ2 (x)

2dx =1.

sin

nπ

2 l

2πn

∫An

x dx = An ∫

1−cos

x dx =

An l =1.

Следовательно, An = 2/l . Для волновой функции ψ2 получим нормированное выражение

ψ2 =	2 sin(	πn x).
	l	l

Плотность вероятности обнаружения частицы в состояниях, описываемых найденной ψ–функцией, по определению равна

w = dWdx

Вероятность dW обнаружить частицу в интервале dx равна

dW = wdx = ψ(x)ψ*(x)dx = ψ2 dx = 2sin2 (nπxl)dx . l

ψ(x), ψ* (x) - комплексно сопряженные значения ψ(x)-функции.

Состояния электронов, описываемые этой функцией, являются стационарными состояниями. На рис. 2.4 приведены графики: (а) - значений энергии En, (б) - волновых функций ψn(x) и (в) - плотностей распределения вероятности wn(x) = |ψn(x)|2.

E	n			ψ	(x)			w (x)
	n			n				n
		n=3
		n=2
		n=1	x				x	x
0			x				x	x
0
		a)			б)			в)
				Рис. 2.4
График		w	(x)= ψ	(x)2 = ψ		n	(x)ψ*n (x)	характеризует
		n	n			n

распределение вероятности обнаружения частицы внутри ямы при различных значениях энергии частицы. Как видно из рисунка, в низшем энергетическом состоянии n =1 (основное состояние) с наибольшей вероятностью можно найти частицу около середины ямы, а вероятность найти ее у стенок равна нулю. Этот результат резко отличается от того, который можно ожидать для макроскопической частицы. Классическую частицу с равной вероятностью можно найти в любом месте пространства.

Задача 2.12. Показать, что спектр энергии свободной частицы с периодической ψ-функцией непрерывен.

Решение. Для свободной частицы волновая функция имеет вид ψ(x)= Aeikx , где k -волновое число. Если на концах участка длиной l

ψ-функция имеет одинаковое значения, то есть является

периодической,

то

ψ(x)= ψ(x +l)

(квантование

на длину

периодичности).

Следовательно

Aeikx = Aeik (x+l ).

Это

означает, что

eikl =1. Используя формулу Эйлера, получим

eikl = coskl +sinkl =1;

isinkl = 0; coskl =1.

Следовательно,

kl = 2πn; k =

2πn

; k2

4π2 n2

2mE

Откуда получим выражение для энергии частицы

E =

n2h2

, где n =1,2,3...

2ml2

Если частица имеет макроскопические размеры, то несмотря на малую массу частицы, спектр энергии практически непрерывен. Расстояние между энергетическими уровнями:

E = h2 ((n +1)2 − n2 )= h2 (2n +1)≈ 0 . 2ml2 2ml2

Задача 2.13. Моноэнергетический поток электронов с энергией Е падает на низкий ( E >U0 ) потенциальный барьер бесконечной ширины

(рис.2.5).

Записать стационарные уравнения Шредингера. Представить вид их решения. Найти коэффициенты отражения и прозрачности барьера.

Решение. Движении

электронов происходит в двух

областях:

1) U = 0(х < 0)

2) U =U0 (x ≥ 0)

Уравнения Шредингера для

этих областей:

′′

2mE

ψ1 = 0 (m – масса

ψ1 +

электрона)

Рис. 2.5.

2m(E −U0 )

ψ′2′ +

ψ2 = 0

2mE

2m(E −U0 )

Учитывая, что

= k2

где k1, k2 - волновые числа, решения уравнений Шредингера представим в виде:

(x)= a eik1x +b e−ik1x (x < 0)

(x)

= a eik2x

+b e−ik2x (x > 0)

где а и b - амплитуды волн.

Слагаемые правой части функции ψ(x) можно рассматривать

как суперпозицию двух волн (прямой и отраженной), но так как в

области 2 нет отраженной волны, то b = 0. Значит ψ

(x)= a eik2x

Воспользуемся условием непрерывности ψ-функции и ее первой

производнойψ′на границе раздела:

ψ1

(x = 0)= ψ2

(x = 0) a1

+b1 =a2

ψ1′

(x = 0)= ψ′2

(x = 0) ik1

(a1 −b1)=ik2a2

(k1 + k2 )

a1 =

1+ k

(k1 − k2 )

b1 =

−

Коэффициент отражения R равен отношению интенсивностей отраженной и падающей волн, а те в свою очередь пропорциональны квадратам амплитуд:

R= b1 2 = k1 − k2 2

a1 k1 + k2

Коэффициент прозрачности:

		− k2		2		4k1k2
k1
D =1− R =1−					=
	k	+ k	2			(k + k	2	)2
1						1

D всегда больше нуля.

Задача 2.14. Моноэнергетический поток электронов с энергией Е

падает на высокий ( E <U0 )

потенциальный барьер бесконечной ширины (рис.2.6). Записать уравнения Шредингера, представить вид их решения. Найти распределение плотности вероятности w(x).

I Е II

0 х

Рис. 2.6.

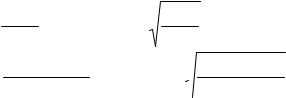
Решение. Стационарные уравнения Шредингера для областей 1

и 2:

′′	+	2mE	ψ1 = 0; k1 =	2mE
ψ1	+	h2	ψ1 = 0; k1 =	h2

ψ′2′ − 2m(Uh02 − E) ψ2 = 0; k2= 2m(Uh02 − E)

Решение уравнений:

ψ1(x)= a1eik1x +b1e−ik1x

ψ2 (x)= a2ek2x +b2e−k2x

Так как при

x → ∞, слагаемое a eik2x

→∞, а это нарушение

свойства ограниченности функции ψ2 (x). Тогда a2 = 0 и

(x)= b e−k2x .

Используем

свойства

непрерывности

функций и их

производных:

ψ1

(x = 0)= ψ2

(x = 0) a1

+b1 =b2

ψ1′

(x = 0)= ψ′2

(x = 0) ik1

(a1 −b1)= −k2b2

a −b =−1 k2

b , но

−1

= i , то есть a −b =i k2

i k

Решаем систему двух уравнений, получим

+i k

b1 =

−i k

Из этих выражений следует, что a1 и b1- комплексно сопряженные числа. Их можно представить в виде, не связанном с b2 :

a1 =aeiϕ

b1 = ae−iϕ; ϕ = const

Используя уравнения Эйлера:

a1 =a(cosϕ+isinϕ), b1 = a(cosϕ−isinϕ)

b2 = a1 +b1 = 2acosϕ

Тогда решения уравнений Шредингера:

ψ1(x)= aeiϕeik1x + ae−iϕe−ik1x =aei(k1x+ϕ) + ae−i(k1x+ϕ) =

=a[cos(k1x + ϕ)+ isin(k1x + ϕ)+ cos(k1x + ϕ)−isin(k1x + ϕ)]= 2a cos(k1x + ϕ).

Это косинусоида.

ψ2 (x)= b2e−k2x = 2acosϕ e−k2x .

Это экспонента.

Плотность вероятности электронов вдоль оси х:

w(x)= ψ(x)2

w1(x)= 4a2 cos2 (k1x + ϕ), при x = 0 w1(0)= 4a2 cos2 ϕ

w2 (x)= 4a2 cos2 ϕ e−2k2x , при x = 0 w2 (0)= 4a2 cos2 ϕ

w1(0)= w2 (0)

Графическая интерпретация ψ(x) и w(x)

w(x)

ψ(x)

0	х	0	х
Рис. 2.7.		Рис. 2.8.

Задача 2.15. Частица с массой m и энергией E налетает слева на высокий ( E <U0 ) потенциальный барьер конечной ширины l

(рис.2.9).
а)	Найти		коэффициент
прозрачности		барьера		D для
частицы (m, E)
б)	вычислить		вероятность
прохождения			через	барьер
U0	=10 эВ	и		l =10−8 см

электрона (E = 5 эВ) и протона

(E = 5 эВ).

в) Записать вид функции w(x)

III

0 х

Рис. 2.9.

Решение. Запишем стационарные уравнения Шредингера для трех областей ( x < 0; 0 ≤ x ≤ l; x > l ) области 1 и 3:

	′′		2mE	ψ1,3	= 0; k =		2mE
ψ1,3 + h2							h2
ψ′2′ +			2m(E −U0 )			ψ2 = 0; k2=		2m(E −U0 )

			h2					h2
Решения этих уравнений:
ψ	(x)= a eikx +b e−ikx
	1	1			1
ψ	2	(x)= a ek2x +b e−k2x
		2			2
ψ	3	(x)= a eik (x−l )
		3					ψ3 (x)
Волновой				функции				только одно слагаемое,	так как в
области 3 частица может двигаться только слева направо.									ψ-функций
Для нахождения соотношений между амплитудами

воспользуемся условиями непрерывности ψ-функций и их первых производных.

ψ1(0)= ψ2 (0) a1 +b1 =a2 +b2

(l)= ψ

(l) a ek2l +b e−k2l = a

ψ1′(0)= ψ′2 (0) ik

(a1 −b1)= k2 (a2 −b2 )

ψ′2 (l)= ψ′3(l) k2 (a2ek2l −b2e−k2l )

= ika3

+b =a

−b =

−b )

Выразим

через a3 ,

так

как коэффициент прозрачности

Для этого, во-первых. решим систему, исключив

барьера D = a

−i =1 i .

b1 . Учтем сначала, что

2a1 =i kk2 (b2 − a2 )+ a2 +b2 =i kk2 b2 −i kk2 a2 + a2 +b2 = a2 1−i kk2 +b2 1+i kk2

1−i

Вторая система:

k2l

−k2l

a2e

+b2e

= a3

k2l

−k2l

k2 (a2e

−b2e

)=ika3

или

a2ek2l +b2e−k2l = a3

a2ek2l −b2e−k2l = kik a3

Исключим вычитанием a2

b2e−k2l +b2e−k2l = a3 − ik a3 k2

−k2l

a3 1

− k

2b2e

= a3 1−

; b2

−k2l

Теперь исключим сложением

k2l

2a2e = a3 +

= a3 1

a3 1

2ek2l

Тогда a1 = f (a3 )

1−

k2l

−k2l

Так как k2l >>1 и e−1k2l = ek2l , то первым слагаемым этой суммы можно пренебречь, то есть

1−

e 2

a ≈

Коэффициент прозрачности барьера D:

−2k

2 e

D = a

≈

Так как

k =

, то

U0 − E

−2l

D ≈ Ce h

		16			k2
2m(U0	−E )	16			k2
2m(U0	−E )	, где C =			k2			≈1
						2
					k	2	2
						2
				+		2
			1	+		2
					k2

Для электрона De ≈ 0,267 вероятность проникновения через барьер существенна, а для протона De ≈10−47 ничтожно мала.

Задача 2.16. На пути электрона с длиной волны де Бройля

λ =1,5A находится потенциальный барьер высотой U0 = 40 эВ. Определить длину волны де Бройля после прохождения барьера.

Решение. Движение электронов в направлении х разбиваем на две области. В области I х < 0 U (x)= 0, поэтому электрон движется как свободная частица. Уравнение Шредингера в области I имеет вид

ψ1′′+ k12 ψ1 = 0,

где

k = 2mE h2 =

2π λ ,

λ =1,5A. Отсюда найдем энергию

электрона

(6,62 10−34 )2

E =

4π2h2

= 66,9эВ.

2mλ21

2 9,1 10−31 (1,5 10−10 )2 1,6 10−19

Для области II х > 0 U (x) = U0 уравнение Шредингера имеет вид

ψ′2′ + k22ψ2 = 0, где k2 =

2m(E −U0 ) h2 = 2π λ2 . Отсюда найдем

λ2 =

2πh

2m(E

−U0 )

2m(E −U0 )

6,62 10

−34

2 9,1 10−31(66,9 − 40) 1,6 10−19 = 2,37A.

Задача 2.17. Поток моноэнергетических электронов с энергией Е = 149 эВ падает на высокий прямоугольный потенциальный барьер бесконечной ширины высоты U0 = 150 эВ (см. рис 2.6). Рассчитать относительную вероятность нахождения электрона на расстояниях:

о	о	о	о
x1 =1А, x1	=1А, x2	= 5А, x3	=10А от границы барьера.

Решение. Оценим относительную вероятность обнаружения частицы в области II при указанных в условиях задачи значениях х. Относительная вероятность рассчитывается по формуле

| ψ2 |2 a22 = e−2k2х , где k2 = 2m(U0 − E) h2 .

При заданной разности U0 – Е = 1 эВ = 1,6 10-19 Дж и m = 9,1 10-31 кг получим:

x1 =1А; e−2k2х1 = e−1,028 = 0,358

x2 = 5А; e−2k2х2 = e−5,2 = 0,005

x3 =10А; e−2k2х3 = e−10,28 = 3,43 10−5.

С увеличением х вероятность обнаружения частицы в области II экспоненциально убывает.

2.3.Задачи для самостоятельного решения

2.18.Вычислить длину волны де Бройля электрона, движущегося со скоростью v = 7,4 108 см/с.

2.19.Найти отношения длин волн де Бройля электрона и протона, прошедших ускоряющую разность потенциалов U =1000B.

2.20. Заряженная частица, ускоренная разностью потенциалов

U0 = 200Bимеет длину волны де Бройля λ = 0,0202A. Найти массу

частицы, если известно, что ее заряд численно равен заряду электрона. 2.21. Вычислить длины волн де Бройля электрона λ1 , протона λ2

иатома урана 238 U λ3 , имеющих кинетическую энергию T = 100 эВ.

2.22.Какую энергию E необходимо дополнительно сообщить

электрону, чтобы его длина волны де Бройля уменьшилась от λ1 =1,0A

до λ2 = 0,5A.

2.23. На грань кристалла никеля падает пучок электронов. Кристалл поворачивают так, что угол скольжения меняется. Когда этот угол равен θ = 64°, наблюдается максимальное отражение электронов, соответствующее максимуму первого порядка. Приняв расстояние

между атомными плоскостями d = 2A , определить скорость электронов.

2.24. При	увеличении	энергии электрона	на	E = 200 эВ его
длина волны	де Бройля	изменилась в	η= 2	раза. Найти

первоначальную длину волны электрона.

2.25. Найти длину волны де Бройля молекул водорода, движущихся с наиболее вероятной скоростью в газе при температуре

Т = 20°С.

2.26. Протон с длиной волны λ2 =1,7пм упруго рассеялся под

углом 90° на первоначально покоившейся частице, масса которой в n = 4 больше массы протона. Определить длину волны λ1 рассеянного

протона.

2.27. Поток моноэнергетических электронов падает нормально на диафрагму с узкой щелью шириной b = 2 мкм. Найти скорость

электронов, если на экране, расположенном от щели на расстоянии l = 50 см ширина центрального дифракционного максимума

x = 0,36 мм.

2.28.Найти кинетическую энергию электронов Т, падающих нормально на диафрагму с двумя узкими щелями, если на экране,

отстоящем от диафрагмы на l = 75 см расстояние между соседними максимумами x = 7,5 мкм. Расстояние между щелями d = 25 мкм.

2.29.Узкий пучок моноэнергетических электронов падает под углом скольжения θ = 30° на естественную грань монокристалла алюминия. Расстояние между соседними кристаллическими плоскостями, параллельными этой грани монокристалла, d = 0,2 нм.

При каком ускоряющем напряжении U0 наблюдается максимум зеркального отражения? Известно, что следующий максимум

зеркального отражения возникает при увеличении ускоряющего напряжения в η= 2,25 раза.

2.30.Пучок электронов с кинетической энергией Т = 180 эВ падает нормально на поверхность монокристалла никеля. В

направлении,	составляющем угол α	= 55° нормалью к поверхности,
наблюдается	максимум отражения	четвертого порядка. Найти

межплоскостное расстояние d, соответствующее этому отражению.

2.31.Электрон движется по окружности радиуса R = 0,5 см в однородном магнитном поле с индукцией В = 8 мТл. Определить длину волны де Бройля для электрона.

2.32.Определить длину волны де Бройля для электрона находящегося на второй орбите атома водорода.

2.33.С какой кинетической энергией движется электрон, если длина волны де Бройля равна его комптоновской длине волны?

2.34.Релятивистская частица с массой m движется с кинетической энергией T. Найти длину волны де Бройля частицы.

2.35.Вычислить волну де Бройля релятивистских электронов, подлетающих к катоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра равна

λк =10пм.

2.36. При каких значениях кинетической энергии электрона и протона ошибка в вычислении длины волны де Бройля по нерелятивистской формуле не превышает 1%?

2.37.	Пучок электронов, ускоренный разностью потенциалов
U0 =133B	падает под углом θ = 45° на естественную грань

монокристалла серебра. При этом вертикально отраженный пучок образует максимум третьего порядка. Межплоскостное расстояние

d = 2A . Найти внутренний потенциал серебра. Внутренний потенциал кристалла U0 = Aвых е .

2.38. Какова энергия нейтрона Т, имеющего длину волны

λ = 2A ? При какой температуре T1 его энергия при тепловом равновесии имела бы эту величину?

2.39. Оценить кинетическую энергию, которой должны обладать на выходе из ускорителя электроны, для того, чтобы они могли в экспериментах по рассеянию эффективно использоваться для исследования внутренней структуры объектов с линейными размерами

	o	(атом),	2) λ =10−15 м(атомное ядро). Во втором
порядка 1) l ≈1A		(атом),	2) λ =10−15 м(атомное ядро). Во втором
случае считать,		что	электрон релятивистский, то есть
	hc
λ =	T (T + 2m c2 ).
	0

2.40.В опытах по дифракции электронов на поликристаллической фольге найдено, что диаметр дифракционного кольца, соответствующего отражению первого порядка от плоскостей с межплоскостным расстоянием d, равен D = 3 см. Расстояние от фольги до экрана l =15 см. Энергия электронов равна Т = 200 эВ. Найти величину d.

2.41.Пучок электронов с энергией Т проходит через тонкую поликристаллическую золотую фольгу, а затем попадает на фотопластинку. Области почернения на пластинке имеют форму концентрических колец с центрами на оси пучка. Рассчитать радиусы

первого и второго колец, если расстояние от фольги до пластинки l = 10 см, d = a 2 , где постоянная решетки a = 2,88 10−10 м.

2.42.Оценить наименьшие ошибки с которыми можно


определить	скорость		электрона	v1 , протона	v2 и шарика v3
массой m = 1 мг,			если их координаты установлены с
неопределенностью		x =1 мкм.
2.43. Оценить неопределенность скорости электрона						v в атоме
водорода,	полагая	размер атома		l = 0,1 нм,	x ≈ l 2.	Сравнить

полученное значение v со скоростью электрона v1 на первой

боровской орбите 2.44. В некоторый момент область локализации свободного

электрона x0 = 0,1 нм. Оценить ширину области локализации этого электрона x спустя промежуток времени t = 1c. Масса электрона

m= 9,1 10−31 кг.

2.45.Во сколько раз длина волны де Бройля λ меньше неопределенности ее координаты x , которая соответствует относительной неопределенности импульса в 1%.

2.46. Предполагая, что неопределенность координаты x движущейся частицы равна длине волны де Бройля λ, определить

относительную неопределенность импульса	p p этой частицы.
2.47. Оценить, имеет ли смысл понятие траектории электрона в
камере Вильсона, летящего со скоростью	v = 1 км/с , если толщина

следа x ≈10−1мм.

2.48.Оценить минимальную кинетическую энергию Тmin электрона, локализованного в области размером l = 0, 1 нм.

2.49.Электрон с кинетической энергией Т = 10 эВ локализован в области l = 0, 1 мкм. Найти относительную неопределенность

скорости электрона. Считать x = l2.

2.50.Оценить кинетическую энергию нуклона в ядре, полагая радиус ядра r ≈10−13 cм.

2.51.Частица массы m локализована в области размером l. Оценить кинетическую энергию T частицы, при которой ее относительная неопределенность будет около 0,01.

2.52. Используя соотношение неопределенности

x p ≈ h

оценить низший энергетический уровень электрона в атоме водорода. Принять x ≈ l2, где линейный размер атома l = 0, 1 нм .

2.53.	Приняв, что минимальная	энергия	нуклона в	ядре
Е = 10 МэВ, оценить линейные размеры ядра.
2.54.	Атом испустил фотон с	длиной	с длиной	волны
λ = 0,58 мкм	за время τ =10−8c. Оценить неопределенность			x с

которой можно установить координату фотона в направлении его движения, а также относительную неопределенность λλ его длины

волны.

2.55. Типичное время жизни τ возбужденных ядер имеет порядок 10−12 c . Найти неопределенность энергии E (в МэВ) испускаемых γ- лучей.

2.56. Свободно движущаяся нерелятивистская частица имеет относительную неопределенность кинетической энергии TT .

Оценить, во сколько раз неопределенность координаты x такой частицы больше ее волны де Бройля λ.

2.57. Оценить относительную ширину спектральной линии ωω, если время жизни атома в возбужденном состоянии τ ≈10−8c, а длина волны излучаемого фотона λ = 0,6мкм.

2.58. Написать стационарное уравнение Шредингера для линейного гармонического осциллятора. Учесть, что сила, возвращающая частицу в равновесие F = −bx , где b - коэффициент пропорциональности, х - смещение.

2.59.Написать уравнение Шредингера для свободного электрона, движущегося в положительном направлении оси х со скоростью v.

2.60.Основное состояние электрона в электростатическом поле

ядра атома водорода описывается радиальной волновой функцией

− r

R(r) = A e r1 , где A - некоторая постоянная, r1 - первый боровский

радиус. Найти расстояние r от электрона до ядра, при котором плотность вероятности w(r) имеет максимальное значение.

2.61. Состояние частицы описывается волновой функцией ψ(x) = A exp(–αx2), где α - положительная постоянная. Найти нормировочный коэффициент A.

2.62.Найти нормировочный коэффициент A для волновой функции ψ(x) = A sin(k x), которая удовлетворяет граничным условиям

ψ(a) = ψ(b) = 0.

2.63.Основное состояние электрона в электростатическом поле

ядра		атома			водорода			описывается		радиальной	волновой
функциейR(r) = A exp(− r r1 ),								где A	-	некоторая	постоянная,
r1 =	4π ε0h2			-	первый боровский				радиус. Найти		вероятность
		m å2

обнаружения электрона в области r ≥ 2r1.
		2.64. Радиальная волновая функция некоторой частицы имеет
видR(r) =			A			r
				exp	−		, где r - расстояние от этой частицы до силового
			r
						a

центра, A и a - постоянные. Определить коэффициент A.

2.65.Электрон находится в возбужденном состоянии,

		r	−	r
				2r
	−		е	1	,
		2r
описываемом радиальной волновой функцией: R(r) = A 1
		1

где r1 - радиус первой боровской орбиты. Найти нормировочный коэффициент А.

2.66.Электрон находится в возбужденном состоянии,

			r	−	r
					2r
описываемом радиальной волновой функцией:		−		е	1	,
			2r
	R(r) = A 1
			1

где r1 - радиус первой боровской орбиты. Найти значение r, при котором плотность распределения вероятности w(r) имеет максимальное значение.

2.67. Частица массой m находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти энергию частицы E в стационарном состоянии, описываемом волновой функцией, пропорциональной sin kx , где k - заданная постоянная, x - расстояние от одного края ямы.

2.68. Частица массой m находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти: 1) массу частицы, если ширина ямы l и разности энергий третьего и второго энергетических уровней равна E ; 2) квантовое число n энергетического уровня частицы, если интервалы энергии до соседних

сним верхнего и нижнего уровней относятся как η:1, где η=1,4.

2.69.Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками

шириной l.	Найти вероятность W обнаружения частицы		в области
l 3 < x < 2l 3.
2.70. Частица массой m находится в основном состоянии в
одномерной	прямоугольной потенциальной яме	с	бесконечно

высокими стенками. Максимальное значение линейной плотности вероятности нахождения частицы равно wmax. Найти ширину ямы l и энергию частицы в этом состоянии.

2.71. Электрону в потенциальной яме шириной l	отвечает
волновое число k = πn l, n =1,2,3.... Используя связь	энергии

электрона E с волновым числом k получить выражение для собственных значений энергии En .

2.72. Частица находится в потенциальной яме с бесконечно высокими стенками. Найти отношение разности соседних

энергетических	уровней	к энергии частицы в трех случаях: 1) n = 3;
2) n = 10; 3)	n → ∞.	Пояснить физический смысл полученных

результатов.

2.73. Электрон находится в прямоугольной потенциальной яме с бесконечно высокими стенками шириной l = 0,5 нм. Найти (в эВ) наименьшую разность Emin энергетических уровней электронов.

2.74. Собственная функция, описывающая состояние частицы,
имеет вид	ψn	(x)= C sin(nπx l).		Используя		условия	нормировки,
определить постоянную С.
2.75. Решение уравнения Шредингера для бесконечно глубокой
потенциальной		ямы	можно		записать		в	виде
ψ(x)= C eikx	+ C	e−ikx , где k =	2mE h2		. Используя граничные условия
1	2
и условия	нормировки		определить 1)			коэффициенты		C1 и C2
2) собственные значения энергии				En	3) выражение для собственной
нормированной		ψ-функции.

2.76.В одномерной потенциальной яме шириной l находится электрон. Вычислить вероятность W обнаружения электрона на первом энергетическом уровне в интервале l/4, равноудаленном от стенок ямы.

2.77.Вычислить отношение вероятностей W1 W2 нахождения

электрона на первом и втором энергетических уровнях в интервале l/4, равноудаленном от стенок ямы.

2.78. Электрон находится в прямоугольной потенциальной яме с бесконечно высокими стенками шириной l . Определить среднее значение координаты электрона (0 < x < l).

2.79. Зная	решение	уравнения	Шредингера		для			низкого
потенциального	барьера	ψ (x)= A eik1x + B e−ik1x			, ψ	2	(x)= A e−k2x
		1	1	1		2		2

определить из условия непрерывности ψ-функций и их производных

на границе барьера отношение амплитуд B1 A1 и A2 A1 .
2.80. Зная отношение		амплитуд B1		A1 = (k1 − k2 ) (k1 + k2 )		для
волны,	отраженной от барьера и		A2 A1 = 2k1	(k1 + k2 )	для проходящей
волны,	найти выражения	для	коэффициента		отражения	R и

коэффициента прохождения D.

2.81.На пути электрона с длиной волны де Бройля λ1 =1A находится потенциальный барьер высотой U0 =120 эB. Определить длину волны де Бройля λ2 после прохождения барьера.

2.82.Электрон с энергией E =100 эВ падает на потенциальный барьер высотой U0 = 64 эВ. Определить вероятность W того, что

электрон	отразиться от	U(x)
барьера.	I	U(x)	II

2.83. Определить коэффициент преломления

волн де Бройля на границе T потенциальной ступени (рис. 2.10). Кинетическая

60	0	x

Рис. 2.10.

энергия протонов T =16 эВ, а высота потенциальной ступени - U0 = 9 эВ.

2.84.Коэффициент отражения протона от потенциального барьера R = 2,5 10−5 . Определить, какой процент составляет высота барьера U0 от кинетической энергии Т подающих на барьер протонов.

2.85.Вывести формулу связывающего коэффициент преломления n на граница низкого потенциального барьера и коэффициент отражения R от него.

2.86.Электрон с энергией E =10 эВ падает на прямоугольный

потенциальный барьер. Определить высоту барьера U0 , при которой

показатель преломления волн де Бройля n численно равен коэффициенту отражения R.

2.87.Кинетическая энергия электрона в два раза превышает высоту потенциального барьера. Определить коэффициент отражения R и коэффициент прохождения D электронов для барьера.

2.88.Коэффициент прохождения электронов через низкий потенциальный барьер равен коэффициенту отражения D = R. Определить, во сколько раз кинетическая энергия Т электронов больше высоты потенциального барьера U0 .

2.89.Вывести формулу, связывающую коэффициент прохождения D электронов через потенциальный барьер и коэффициент преломления n волн де Бройля.

2.90.Коэффициент прохождения протонов через потенциальный барьер D = 0,8. Чему равен показатель преломления n волн де Бройля на границе барьера?

2.91.Вычислить коэффициент прохождения D электронов с

энергией		E =100 эВ		через			потенциальный		барьер с	высотой
U0	= 99,75 эВ.
	2.92. Для областей I					и II	высокого потенциального барьера (см.
рис.		2.6)	волновые					функции	имеют	вид
ψ	(x)= A eik1x + B e−ik1x , ψ			2	(x)= A e−kx .			Используя	непрерывность ψ-
1	1	1				2

функций и их первых производных на границе барьера, найти отношения амплитуд A2 A1 .

2.93. Электрон проходит через прямоугольный потенциальный барьер шириной d = 0,5 нм. Высота барьера больше энергии электрона на 1%. Вычислить коэффициент прозрачности D для случаев

1) E =10 эВ; 2) E =100 эВ.

2.94. Ширина прямоугольного барьера. d = 0,2 нм. Разность энергий U0 − E =1 эВ. Во сколько раз изменится вероятность

прохождения электрона через барьер, если разность энергий возрастет

в10 раз?

2.95.При какой ширине d прямоугольного потенциального барьера коэффициент прозрачности для электронов D = 0,01. Разность энергий U0 − E =10эВ.

2.96.Электрон с энергией Е движется в положительном направлении оси х. При каком значении U0 − E , выраженном в эВ

коэффициент прозрачности D = 0,001, если ширина барьера d = 0,1 нм? 2.97. Электрон с энергией E = 9 эВ движется в положительном

направлении оси х. Оценить вероятность W того, что электрон пройдет через потенциальный барьер, если его высота U0 =10 эВ и ширина

d = 0,2 нм.
2.98. Прямоугольный	потенциальный барьер имеет ширину
d = 0,1 нм. При какой	разности энергий U0 − E вероятность

прохождения электрона через барьер W = 0,99.

3. Основы квантовой физики атомов

3.1.Основные понятия и законы

Теория Бора для атома водорода и водородоподобных ионов

Первый постулат Бора: существуют некоторые стационарные состояния атома водорода, находясь в которых он не излучает энергии. Этим стационарным состояниям соответствуют вполне определенные (стационарные) орбиты, по которым движется электрон.

Второй постулат Бора: при переходе атома из одного стационарного состояния в другое испускается или поглощается квант энергии. Излучение происходит при переходе электрона в атоме из состояния с большей энергией в состояние с меньшей энергией

Еn - Еm = Е = hν. (3.1)

Третий постулат Бора: в стационарном состоянии атома, когда электрон находится на с орбите с энергией En, момент импульса электрона принимает дискретные значения, удовлетворяющие условию:

Ln = mvr = nh, где n = 1,2,3,…	(3.2)
Здесь m – масса электрона, v - скорость электрона,	r - радиус его

орбиты, n - главное квантовое число (номер энергетического уровня), h - постоянная Планка.

Целое число n равно количеству длин волн де Бройля для электронов, укладывающихся на длине стационарной орбиты, т.е.

отношению длины окружности к длине волны де Бройля.										(3.3)
	2πr	=	2πrmv			= mvr			= n.	(3.3)
		=		h		= mvr			= n.
	λ			h				h
Второй закон Ньютона для							электрона в атоме или ионе с Z ≥1
(He+ Z=2, Li++ Z=3) имеет вид					2		2			(3.4)
				Ze	2		2			(3.4)
	F =			Ze			=	mvn	,
	F =			4πε r2			=	r	,
				4πε r2				r
				0 n				n

Из (3.2) и (3.4) получим энергию электрона, находящегося на n-ой

боровской орбите:	2		4	(3.5)
	2			(3.5)
En = −	mZ	e		1	.




8ε2h2				n2
	0

Скорость электрона, находящегося на n-ой боровской орбите:

(3.6)

2ε0h

Радиус орбиты

ε0h2

(3.7)

r =

n2.

πmZ

Обобщенная сериальная формула Бальмера-Ридберга

= Z

Rλ

−

(3.8)

ν = Z

Rν

−

где Rλ =1,097 107 м−1, Rν = Rλc = 3,288 1015 с−1 - постоянные Ридберга, ni

– номер энергетического уровня, с которого электрон переходит в спектре испускания, nf - номер энергетического уровня, на который электрон переходит в спектре испускания (nf < ni).

В атоме водорода переход на энергетический уровень n = 1 – соответствует серии Лаймана, n = 2 - серии Бальмера, n = 3 - серии Пашена, n = 4 - серии Бреккета (рис. 3.1).

0 -0,38 -0,54

-0,85 -1,51

-3,4

-13,6

En/Z2 (эВ)

Пашена

Бальмера

серия Лаймана

n=∞ n=6

n=5 n=4

n=3

n=2

n=1

Рис. 3.1.

Энергия ионизации – это та энергия, которую необходимо сообщить электрону, находящемуся в основном состоянии (в состоянии с наименьшей энергией), чтобы он перешел на бесконечно

удаленный уровень, т.е. атом превратился в ион. Для атома водорода энергия ионизации равнаEион = E∞ − E1 = 0 − (−13,6) =13,6эВ.

Атом водорода и водородоподобные ионы в сферических координатах. Квантовые числа

декартовых

координатах

неудобно

описывать

движение

электронов

атоме

водорода

водородоподобных ионов

(He+,

Li++).

Его

потенциальная

энергия

E = −

Ze2

зависит только

4πε0r

от расстояния электрона до

Рис.3.2.

ядра.

Поле

является

центрально-симметричным.

Поэтому для описания

движения

электрона

можно

выбрать

сферическую систему координат с центром, расположенным в ядре

(рис.3.2).

Здесь

x = rsin

θ sinϕ; y = rsinθ cosϕ

(3.9)

z = r cosθ; Ψ(x, y,z) = Ψ(r,θ,ϕ).

Уравнение Шредингера для стационарных состояний в

сферических координатах

∂

2 ∂Ψ

∂

∂Ψ

1 ∂2Ψ

sinϑ

sin

θ ∂ϑ

∂r

sin

θ ∂ϑ

∂ϑ

(3.10)

(E −U )Ψ = 0,

где Ψ = Ψ(r,θ,ϕ)- волновая функция, E - полная энергия частицы, U - потенциальная энергия частицы (являющаяся функцией координат).

Символическая запись Ψ -функции, описывающей	состояние
электрона и атома водорода
Ψn,l,m (r,θ,ϕ)	(3.11)

где n,l,m – квантовые числа: главное, орбитальное, магнитное.

Будем искать волновую функцию Ψ = Ψ(r)

в виде произведения

функций R(r)

только

от

радиуса и F(θ,ϕ)

только

от угловых

координат θ,ϕ.

Ψ(r)= R(r)F(θ,ϕ)

(3.12)

Подставляем это произведение в (3.10) и умножая все члены на

r2 RF .

Можем переписать уравнение в виде

1 d 2 dR

8π2m

Ze2

4πε0r

R dr

(3.13)

∂

∂F

∂2F

= −

sinθ

−

= λ,

F sin2

θ ∂ϕ2

F sinθ ∂θ

∂θ

Первая часть есть функция только от r , а вторая – только от

θ,ϕ, поэтому равенство их при всех значениях

r,θ,ϕ, и

возможно

лишь в том случае, если каждая из частей равенства есть постоянная величина, обозначенная здесь λ. таким образом, уравнение Шредингера распалось на 2 уравнения, которые можно записать в виде

1 d

8π2m

Ze2

E +

−

R = 0

(3.14)

4πε

r dr

∂

∂F

∂2F

+ λF

sinθ

= 0.

(3.15)

sin2

θ ∂ϕ2

sinθ ∂θ

∂θ

Так как решение трехмерного уравнения Шредингера зависит от

трех чисел n,l,m ,

то волновая функция

Ψ = Ψ(r,θ,ϕ)

может быть

представлена в виде произведения 3-х функций от каждой из сферических координат

Ψn,l,m (r,θ,ϕ)= Rn,l (r)Θl,m (θ)Φm (ϕ)	(3.16)
Здесь Θl,m (θ)Φm (ϕ)= F(θ,ϕ).
Подставляя в 3.15 функцию F(θ,ϕ) в виде	произведения

Θl,m (θ)Φm (ϕ) и умножая все члены на

sin2 θ

, можно переписать это

уравнение в виде

ΘΦ

1 d 2Φ

sinθ d

dΘ

sinθ

+ λsin

θ = −

= m

(3.17)

Φ dϕ2

Θ dθ

dθ

Здесь опять левая часть равенства есть функция только от θ, а правая – лишь от ϕ, следовательно, они могут быть равны друг другу при всех значениях θ и ϕ, если каждая из них есть постоянная,

обозначенная здесь как m2 .Уравнение 3.17 переходит поэтому в 2 уравнения

1 d

dΘ

sinθ

λ −

(3.18)

sin

Θ = 0

sinθ dθ

dθ

		d 2Φ	= −m2Φ.	(3.19)
		dϕ2

Решение последнего из уравнений
Функция Φ(ϕ)		Φ(ϕ)= eimϕ.		(3.20)
	для		ее однозначности	должна быть

периодической с периодом 2π, так как физически ϕ есть один и тот же угол, что и ϕ+ 2π. Такая периодичность будет иметь место, если параметр m равен любому целому числу, положительному или отрицательному, включая нуль:

m = 0, ±1, ± 2...

(3.21)

Решение уравнения (3.16) можно получить в виде

(θ,ϕ)= Pm

(θ)ei

ϕ.

(3.22)

Pm (θ)

l,m

представляют из себя шаровые функции. Некоторые (для

l ≤ 2) показаны в таблице

Fl,m (θ,ϕ)

const

ccosθ

csinθe±iϕ

c(3cos2 θ −1)

csinθcosθe±iϕ

csin2 ϕe±2iϕ

Перейдем к

решению уравнения (3.14) для радиальной части

волновой

функции

Ψ = Ψ(r),

обозначенной R(r). Постоянная

разделения λ в этом уравнении равна l(l +1). Поэтому

1 d

2 dR

8π2m

Ze2

l(l +1)

E +

−

R = 0

(3.23)

4πε

r dr

Выполнив дифференцирование в первом члене и вводя

обозначения

8π2m

πmZe

E = A,

= B ,

(3.24)

можем переписать

ε0h2

l(l +1)

d 2R

2 dR

+ A +

−

R = 0

(3.25)

r dr

Рассмотрим случай электрона, связанного с ядром, когда полная энергия отрицательна, т.е. E < 0 , при этом A < 0.

Подставляя сюда значения А и В убедимся, что это требование равносильно следующему

E =−	2π2mZ 2e4	1	= −	2π2mZ 2e4	1	,	(3.26)
	h2	(l +1)2		h2	n2

В последнем выражении n обозначает целое число, равное l +1, при этом n ≥1, n - главное квантовое число.

Таким образом, в области E < 0 спектр собственных значений энергии дискретный, и эти дискретные собственные значения энергии En совпадают с дискретными значениями энергии по Бору.

Этим собственным значениям энергии соответствуют собственные значения Ψ –функции, определенные целочисленными параметрами n,l,m

(r,θ,ϕ)= R

(r)Θ

(θ)Φ

(ϕ)= Ae−

l,m

eimϕ

n,l,m

n,l

(3.27)

l+i

l−

∑ ai

sin θ

∑

bi cosi

n−l−1

i=0

Целочисленные параметры n,l,m характеризуют состояние электрона в атоме и являются квантовыми числами.

Радиальная часть решения

−	r	n−l−1	2r	l+i
Rn,l (r)= Ae r0		∑ ai	2r		(3.28)
Rn,l (r)= Ae r0		∑ ai	r		(3.28)
		i=0	r
			0

характеризует распределение плотности вероятности электронного облака по радиусу, т.е. распределение плотности вероятности нахождения электрона. Квантовое число n определяет энергию электрона в атоме и может принимать значения 1, 2, 3…, ∞. Переход электрона в состояние с n = ∞ соответствует ионизации атома, электрон в этом случае становится свободным, энергия электрона в этом случае положительна и может принимать любые значения.

Момент импульса электрона, находящегося в состоянии, определяемом квантовыми числами n,l

L = h	l(l +1),	(3.29)
где l - орбитальное квантовое	число, которое может	принимать
значения 0, 1, 2 …n −1 (всего n значений).
Проекция вектора L на направление магнитного поля
Llz = mh,		(3.30)

где m - магнитное квантовое число. Число m может принимать значения 0, ±1, ±2 …±l (всего 2l +1 значений). Соотношение (3.30) отражает принцип пространственного квантования.

Состояние электрона в атоме определяется введенными квантовыми числами n,l,m . Если n =1, то орбитальное квантовое число l = 0, а магнитное квантовое число m = 0. Если n = 2, то орбитальное квантовое число может иметь 2 значения l = 0, l =1. При

этом магнитное квантовое число m может принимать такие значения: если l = 0, то m = 0, а если l =1, то m может принимать 3 значения - m = 0, ±1.

Таким образом, каждому значению энергии En (кроме E1) соответствует несколько волновых функций Ψn,l,m , отличающихся значениями квантовых чисел n,l,m . Например E2 , соответствует

четыре волновые функции Ψ2,0,0 , Ψ2,1,0 , Ψ2,1,−1 , Ψ2,1,1 . Это означает, что электрон в атоме водорода может иметь одно и то же значение энергии, находясь в различных состояниях.

Состояния с одинаковой энергией называют вырожденными, а число различных состояний с одинаковым значением энергии называется кратностью вырождения. Каждому уровню с главным квантовым числом n соответствует n состояний, отличающихся

квантовыми числами	l = 0,1, 2...n −1. Такое вырождение	имеется
только в кулоновском	поле ϕ = k e r . В свою очередь,	каждое

состояние с определенным l вырождено 2l +1 раз по значению m , поэтому общая кратность вырождения стационарного состояния

(стационарного уровня) с квантовым числом n будет ∑n−1 (2l +1)= n2 .

l=1
Так, состояние, относящиеся к различным	значениям
l = 0,1,2...принято обозначать соответственно буквами	s, p, d, f ...

латинского алфавита. Например, состояние с нулевым орбитальным

моментом	(l = 0) называют		s –состоянием, состояние с	l =1 p –
состоянием,		и т.д.. При n =1	имеется одно состояние 1s (l = 0, m = 0),
при n = 2	l	принимает 2 значения, (l = 0, l =1) поэтому		имеется 2

состояния 2s и 2p и т.д.

Рассмотрим спектр функций распределения электрона в водородоподобных атомных системах для различных значений орбитального квантового числа l и для значений главного квантового числа

В s –состоянии (l = 0, m = 0) волновая функция	сферически
симметрична, не зависит от углов θ, ϕ. При l > 0,	т.е. для p –

состояний, d–состояний и т.д. электронное облако уже не будет сферически симметрично, т.к. Ψ(r) будет зависеть от угла θ.

Вероятность того, что электрон находится в области объемом dV в окрестности точки с координатами r,θ,ϕ

dW =

(r,θ,ϕ)

2 dV ,

(3.31)

n,l,m

где

dV = r2 sin θdθdϕdr .

(3.32)

Ψ(r),

Нормированные собственные функции

отвечающие 1s –

состоянию и 2s –состоянию

(r)=

−r

(r)=

−

− r

(3.33)

a ,

2a ,

1,0,0

πa3

2,0,0

4 2πa3

где

качестве единицы

длины

принят

боровский

радиус

a =

4πε0h

= 52,9 пм. Или

e2m

(ρ)=

(r)

e−ρ,

(2 −ρ)e−2 ,

(3.34)

1,0,0

2,0,0

2π

где ρ = ra - безразмерная единица длины.

Вероятность dW найти электрон в атоме водорода находящимся в s –состоянии в интервале (r,r + dr) одинаков по всем направлениям

ми определяется формулой
dW = Ψn ,0,0 (r )2 4πr 2dr	(3.35)

Орбитальный магнитный момент электрона

μl = μ B l(l + 1), где l = 0, 1, 2 …(n -1),

(3.36)

а μB = 2emh = 0,927 10 − 23 Дж/Тл - магнетон Бора.

Многоэлектронные атомы. Спин электрона. Принцип Паули

Релятивистская квантовая теория постулирует, что кроме момента импульса, связанного с движением электрона вокруг ядра, электрон имеет собственный момент импульса, называемый спином.

Спин и спиновый магнитный момент электрона

Ls = h s(s +1), μs = 2μB s(s +1),

где s - спиновое квантовое число. Для электрона, протона и нейтрона s = 1/2, μB - магнетон Бора.

Квантовое число ms определяет проекцию спина на направление магнитного поля (ось Z)

Ls	Z = hms ,	(3.37)

где ms = ±s = ±1/2.

Таким образом, состояние любого электрона в атоме определяется набором 4-х квантовых чисел: n; l; m; ms..

В невозбужденном атоме электроны занимают состояния с возможно низкими значениями энергии. При распределении электронов по состояниям соблюдается принцип Паули, согласно которому в каждом состоянии может находиться не более одного электрона. Другими словами, в атоме не может быть двух электронов с одинаковыми наборами чисел n; l; m; ms.

При заданных значениях n, l существует 2(2l+1) различных состояний, при определенном n - 2 n2 различных состояний. Все состояния с определенным значением n образуют оболочку. Оболочки принято обозначать заглавными латинскими буквами:

n	1	2	3	4	…
Оболочка	K	L	M	N	…

К-оболочка содержат только s-состояния (l = 0), L–оболочка имеет s-(l = 0) и p-(l = 1) подоболочки и т.д. В соответствии с принципом Паули s-подоболочка может содержать не более 2 электронов, p-подоболочка – не более 6, К-оболочка может вместить не более 2 электронов, L–оболочка – не более 8 и т.д..

Значение	0	1	2	3	4	5
орбитального
квантового числа l
Спектроскопический	s	p	d	f	g	h
символ

Электронная конфигурация записывается следующим образом: число, стоящее слева перед спектроскопическим символом, означает главное квантовое число n, а сам спектроскопический символ отвечает тому или иному значению орбитального квантового числа l (например, обозначению 2p отвечает электрон с n =2 и l =1; 2p2 означает, что таких электронов в атоме 2, и т.д.).

В следующей таблице приведено распределение электронов по состояниям для ряда элементов периодической системы. В последней графе записана электронная конфигурация основного состояния.

Элемент	K		L		Электронная
	s	s		p	конфигурация
H	1	-		-	1s
He	2	-		-	1s2
Li	2	1		-	1s22s

Полный момент импульса электрона
Lj = h j(j +1),	(3.38)

где j – внутреннее квантовое число ( j = l + 1/2, l - 1/2) .

Момент импульса атома складывается из моментов всех электронов электронной оболочки. Для большинства атомов из

таблицы Менделеева характерна схема сложения моментов, называемая L–S-связью. Орбитальные моменты отдельных электроновr

складываются в результирующий орбитальный момент атома LL , спиновые моменты электронов – в спиновый момент атома LrS . Затем

результирующие моменты и складываются в полный момент атома
LrJ .
Полный орбитальный момент атома
LL = h L(L +1),	(3.39)
где L – полное орбитальное квантовое число.
Полный спиновой момент атома
LS = h S(S +1),	(3.40)
где S – полное спиновое квантовое число.
Полный момент импульса атома
LJ = h J(J +1),	(3.41)

где J – полное внутреннее квантовое число атома.

Символическое обозначение состояния атома 2S+1LJ . Эту запись

называют спектральным термом, где 2S+1 - мультиплетность. Вместо полного орбитального квантового числа L пишут символ в соответствии с таблицей:

Значение

Символ

Пример.

Терм

расшифровывается

следующим образом:

3/ 2

мультиплетность

2S+1=2,

следовательно

S=1/2,

символу P

соответствует L = 1, а J=3/2.

Магнитный момент атома

μJ = gμB J(J +1),

где g – множитель (или фактор) Ланде,

g =1+	J (J +1)+ S(S +1)− L(L +1)	.

	2J(J +1)

Проекция магнитного момента атома на направления внешнего магнитного поля (совпадающего с осью Z)

				μJ ,Z = gμBmJ ,
где mJ- полное магнитное квантовое число (mJ =J, J-1, …. –J) .
Правило отбора для квантовых чисел S, L, J, mS ,							mL ,mJ
S = 0;		mS = 0;
L = ±1;		mL = 0, ±1;
J = ±1;		mJ	= 0, ±1;			J = 0 → J = 0,		J = 0
Не осуществляются					переходы	J = 0 → J = 0,	а при	J = 0	-
переходы mJ	= 0 → mJ = 0.
Излучение атома происходит при переходе из верхнего
стационарного		уровня		в	нижнее.	При этом испускается		квант	c
энергией hνn n		= En	− En .
2	1		2	1

При записи соответствующих переходов, а также при построении схемы переходов следует учитывать правила отбора квантовых чисел, согласно которым L = ±1; mL = 0, ±1. На примере атома водорода:

Серия Лаймана возникает при переходе электрона с более высоких энергетических уровней n2 = 2, 3... на первый энергетический уровень n1 = 1 (1s -состояние). (см. рис. 3.1.)

Серия Бальмера возникает при переходе электрона в состоянии 2s, 2p (n1 = 2) с более высоких энергетических уровней (n2 > 2). На рис.

3.1показаны переходы, соответствующие сериям Лаймана и Бальмера

сучетом правил отбора ( L = ±1).

Используя спектроскопические обозначения можно записать: Серия Лаймана np →1s ;

ns → 2p

Серия Бальмера nd → 2p ; np → 2s

	Сила, действующая на атом в неоднородном магнитном поле,
		F	=	∂B	μ	(3.42)
	∂B	z		∂z		J ,z
где -	∂B	градиент магнитной индукции.
где -	∂z	градиент магнитной индукции.
	∂z

Решение квантовомеханической задачи о движущемся электроне в поле дает, что энергия состояния зависит от квантовых чисел n и l:

E = −	Za2Rhc	,	(3.43)
	(n −δ)2

Где δ- поправка, зависящая от квантового числа l. Поправку δ называют квантовым дефектом или ридберговской поправкой.

Величина δ для данного элемента убывает с увеличением l. Исходя из (3.43) можно получить выражение для длин волн

спектральных линий, излучаемых при переходе валентного электрона

1			1			1	(3.44)
1	2		1			1
λ	= Za	R	(nf −δf	)2	−	(ni −δi )2	,

Где индекс «f» относится к нижнему, а индекс «i» - к верхнему уровням перехода, ni – номер энергетического уровня, с которого электрон переходит в спектре испускания, nf - номер энергетического уровня, на который электрон переходит в спектре испускания.

Характеристическое рентгеновское излучение

Если один из электронов внутренней оболочки атома удален каким-либо внешним воздействием, например, ударом внешнего быстрого электрона, то на освободившееся место могут переходить электроны из других оболочек. При этом испускается излучение, лежащее в рентгеновском диапазоне.

Любой электрон внутренней оболочки находится в поле ядра с зарядом Ze и тех электронов, которые ближе к ядру. (Влиянием более удаленных от ядра электронов можно пренебречь, поскольку распределение отрицательного заряда близко к сферически симметричному). Энергию электрона в таком поле можно записать в виде

2	(3.45)
E = − Rhc(Z − σ)	,
n2

где поправка σ учитывает экранирующее действие внутренних электронов. Поскольку строение внутренних оболочек у всех атомов одинаковое, поправка σ практически не зависит от Z. Для электрона в K-оболочке σ ≈1, в L-оболочке σ ≈ 7,5.

При переходе электрона из одной внутренней оболочке на

другую испускается излучение с частотой и длиной волны (закон Мозли)

1		(Z −σf )2		(Z −σ	)2		(Z −σ )2		(Z −σ )2 (3.46)
	= R	2	−	i		= R	2	−	2
	= R		−	i		= R		−
λ				2
λ		nf		ni			nf		ni

<<< < Предыдущая 1 2 3 4 5 6 78 / 178 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.2016456.66 Кб4099-112.docx
#
09.02.2016928.47 Кб28adzhienko_v_l_red_ekonomika_chast_1.pdf
#
09.02.2016914.94 Кб187aleksandrovskii_yu_a_psihofarmakoterapiya.doc
#
09.02.2016473.6 Кб65anatom22034-itogovye_testy.doc
#
22.11.201955.19 Кб7Anatomiya_chel_1k_lech_rus_in_1sem.doc
#
09.02.20163.59 Mб598Anisimov_Tretyakova.pdf
#
30.08.2019332.47 Кб42apteka_1.docx
#
09.02.20161.28 Mб2529Attestatsia_proped_otvety.doc
#
14.11.2018498.18 Кб24averages.doc
#
09.02.2016760.98 Кб30bestref-122019.rtf
#
09.02.201672.19 Кб16Bilet.doc