
- •Лекция_8. Модели в переменных состояния
- •8.2. Схемы моделирования
- •8.5. Определение матричных передаточных функций
- •Преобразованные матрицы новой системы координат вычисляются по формулам:
- •Преобразованные матрицы в новой системе координат имеют вид:
- •8.7. Команды MatLab в матричных преобразованиях
Преобразованные матрицы новой системы координат вычисляются по формулам:

Пример 8.6.
Пусть дана система, матрицы
 ,
, и
и которой имеют вид:
которой имеют вид:
 ;
; ;
;
 .
.
В соответствии с уравнением состояния имеем систему скалярных уравнений:
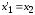 ;
; ;
;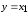 .
.
Структурная схема, соответствующая этим уравнениям, приведена ниже:

Рассмотрим невырожденное преобразование
координат, заданное матрицей
 :
:
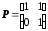 ,
, .
.
Преобразованные матрицы в новой системе координат имеют вид:
 ,
,
 ,
,
 .
.
Дифференциальные уравнения система,
соответствующие матрицам
 ,
, ,
, ,
приведены ниже:
,
приведены ниже:
 (8-22)
(8-22)
По системе уравнений (8-22) составим структурную схему (рис.8.12)

Записывая эквивалентную передаточную функцию по структуре рис.8.11 и рис.8.12 получаем один и тот же результат:
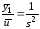 .
.
Этим примером еще раз подтвердим, что между матричными и структурными эквивалентными преобразованиями имеется соответствие, т.е. каждому структурному эквивалентному преобразованию соответствует невырожденное матричное преобразование.
Матрица перехода
 определяет матрицы
определяет матрицы ,
,
 ,
, в новом базисе. При переходе к новому
базису не будем (по возможности)
использовать специальные обозначения
для матриц, записанных в разных базисах.
Формулу преобразования будем понимать
как формулу присваивания одним и тем
же матрицам их значений в разных базисах
и для обозначения операции присваивания
будем пользоваться символом:
в новом базисе. При переходе к новому
базису не будем (по возможности)
использовать специальные обозначения
для матриц, записанных в разных базисах.
Формулу преобразования будем понимать
как формулу присваивания одним и тем
же матрицам их значений в разных базисах
и для обозначения операции присваивания
будем пользоваться символом:
 .
.
Матрицы связанные последним соотношением, определяются как подобные. У этих матриц равны характеристические многочлены, определители и собственные значения. Передаточные функции, связывающие выходные сигналы с входными сигналами, у подобных матриц так же одинаковы.
Как уже указывалось, для конкретной системы можно предложить неограниченное количество моделей в переменных состояния. Желательно так выбрать базис, чтобы матрицы были "удобны", т.е. их легко можно было получить, их удобно использовать при доказательстве теорем, с их помощью просто создать схемы моделирования, а, главное, результаты моделирования просто переносить на физическую модель. Этим требованиям удовлетворяют модели созданные в базисах:
- управляемое каноническое представление (УКП);
- идентификационное каноническое представление (ИКП).
Запись матриц в форме УКП осуществляется относительно просто по дифференциальному уравнению, характеристическому уравнению или передаточной функции.
Пример 8.7.
Дано дифференциальное уравнение системы:
 .
.
Введем обозначения:
 ,
,
 ,
,
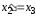 ,
,
 .
.
Отсюда легко получить матрицу
 ,
,
 и
и в формуле УКП:
в формуле УКП:
 ,
, ,
, .
.
Полученные матрицы показывают, что их элементы просто связаны с коэффициентами дифференциального уравнения.
Если первая часть дифференциального уравнения имеет производные от входного воздействия, т.е. числитель передаточной функции определяется некоторым многочленом:

то УКП форма имеет вид:
 ,
, ,
, .
.
Каноническое представление удобно для
моделирования, так как матрицы
 и
и имеют минимальное число ненулевых
элементов (рис.8.13).
имеют минимальное число ненулевых
элементов (рис.8.13).

Идентификационное каноническое представление тех же матриц записывается как:
 ,
,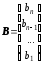 ,
, .
.
Структурная схема моделирования в форме ИКП приведена на рис.8.14.

Сравнение матриц
 ,
,
 ,
, записанных в базисах УКП и ИКП, показывает
пути преобразования матриц. Например,
если уравнения записаны в форме УКП
(матрицы имеют подстрочный символу),
а следует перейти к форме ИКП (матрицы
имеют подстрочный символи), то
необходимо:
записанных в базисах УКП и ИКП, показывает
пути преобразования матриц. Например,
если уравнения записаны в форме УКП
(матрицы имеют подстрочный символу),
а следует перейти к форме ИКП (матрицы
имеют подстрочный символи), то
необходимо:
- чтобы получить матрицу необходимо транспонировать матрицу
необходимо транспонировать матрицу ,
т.е.
,
т.е. ;
;
- чтобы получить матрицу необходимо транспонировать матрицу
необходимо транспонировать матрицу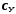 ,т.е.
,т.е. ;
;
- чтобы получить матрицу необходимо транспонировать матрицу
необходимо транспонировать матрицу ,
т.е.
,
т.е. .
.
Переход от базиса УКП к базису ИКП относится к широко используемому, но частному случаю.
В общем случае необходимо уметь любую
матрицу и любой вектор записывать в
разных базисах. Переход к новому базису
осуществляется с помощью матрицы
перехода
 ,
которая, согласно теореме, единственна
и вычисляется по формуле
,
которая, согласно теореме, единственна
и вычисляется по формуле
 (8-23)
(8-23)
где,
 - пара матриц, заданных в исходном базисе;
- пара матриц, заданных в исходном базисе; - пара матриц, заданных в новом
(преобразованном) базисе.
- пара матриц, заданных в новом
(преобразованном) базисе.
Применим эту теорему для определения
матрицы перехода
 от базиса, определяющего матрицы
от базиса, определяющего матрицы ,
,
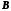 ,
, в форме УКП (обозначим эти матрицы через
в форме УКП (обозначим эти матрицы через ),
к базису, определяющему эти матрицы в
форме ИКП (обозначим матрицы через
),
к базису, определяющему эти матрицы в
форме ИКП (обозначим матрицы через ).
).
.

Так как
 ,
а
,
а ,
то матрица перехода от базиса УКП к
базису ИКП принимает вид:
,
то матрица перехода от базиса УКП к
базису ИКП принимает вид:
 .
.
Пример 8.8.
Даны матрицы системы в форме УКП:
 ;
; ;
; .
.
Записать эти матрицы в форме ИКП.
Для этого
воспользуемся выражением (8-23) и определим
матрицу перехода
 .
Числитель (8-23) определяется выражениями:
.
Числитель (8-23) определяется выражениями:
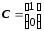 ;
; .
.
Следовательно,
 .
.
Определяем знаменатель выражения (8-23):
 ;
;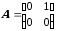 ;
; ;
;
 .
.
Матрица перехода
 определяем как:
определяем как:
 ;
; .
.
Имея матрицу
перехода, определяем матрицы
 ,
,
 ,
,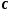 в форме ИКП по формулам:
в форме ИКП по формулам:
 ;
; ;
;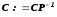 .
.
Подставляя
значения
 и
и ,
получаем:
,
получаем:
 ,
,
 ,
,
 .
.
Эти же матрицы
можно получить, используя свойства
перехода от базиса УКП к базису ИКП, то
есть, транспортируем матрицу
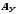 ,
а для получения вектора
,
а для получения вектора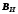 транспортируем вектор строку
транспортируем вектор строку (вектор строка
(вектор строка задана в форме УКП), а для получения
вектора
задана в форме УКП), а для получения
вектора транспортируем вектор столбец
транспортируем вектор столбец ,
который также задан в форме УКП.
,
который также задан в форме УКП.
Для осуществления преобразования подобия решим еще один пример.
Пример 8.9.
Заданы матрицы
 и
и ,
которые следует записать в форме УКП.
,
которые следует записать в форме УКП.
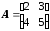 ,
, . (8-24)
. (8-24)
Для
получения матрицы преобразования
 (выражение (8-19)) следует знать матрицы
(выражение (8-19)) следует знать матрицы и
и
 в двух базисах - исходном и УКП. Исходная
матрица задана, а матрицы в форме УКП
получаем через характеристический
многочлен:
в двух базисах - исходном и УКП. Исходная
матрица задана, а матрицы в форме УКП
получаем через характеристический
многочлен:
 .
.
Каноническое представление матриц
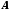 и
и
 в форме УКП имеет вид:
в форме УКП имеет вид:
 ,
, .
.
 ;
; . (8-25)
. (8-25)
Матрицы
 и
и
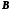 в старом базисе определяются выражением
(8-24), а для их определения в новом базисе
определим матрицу перехода
в старом базисе определяются выражением
(8-24), а для их определения в новом базисе
определим матрицу перехода как:
как:
 . (8-26)
. (8-26)
Определяем составляющие выражения (8-26)
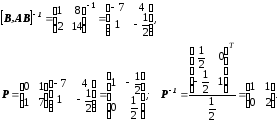
Осуществим проверку. Матрица
 должна приводить матрицу
должна приводить матрицу и
и
 к каноническому виду (форме УКП):
к каноническому виду (форме УКП):
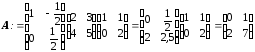 ,
,
 . (8-27)
. (8-27)
Как видно
из этого примера, преобразования подобия,
даже для простой системы, связано с
громоздкими расчетами. В MatLabимеется командаss2ss,
осуществляющая преобразования подобия
при заданной матрицы .
Применение этой команды значительно
упрощает расчеты и будет проиллюстрировано
на конкретных примерах.
.
Применение этой команды значительно
упрощает расчеты и будет проиллюстрировано
на конкретных примерах.
