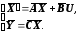8.5. Определение матричных передаточных функций

Уравнение состояния было определено через передаточные функции. При исследовании систем регулирования часто приходится решать обратную задачу: определять передаточную функцию по уравнению состояния. Наиболее просто можно получить передаточные функции системы путем матричных преобразований.

Матрица в этой записи отсутствует, так как в системах регулирования она обычно нулевая. Преобразуем по Лапласу при нулевых начальных условиях матричные уравнения

.

Это уравнение можно привести к виду

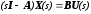
и решить относительно :

(8-14)

Преобразуем по Лапласу и второе уравнение

. (8-15)

Подстановка (8-14) в (8-15) дает

Следовательно, передаточная функция системы может быть определена как отношение изображения по Лапласу выходного сигнала к входному.

В частном случае (рис.8.10) входные и выходные сигналы являются скалярными величинами, и передаточная функция разомкнутой системы выражается через матрицы

. (8-16)

Рассмотрим пример, иллюстрирующий эти преобразования

Пример 8.4.

В примере 8.2 была определена обратная матрица . Подставляя известные значения из (8-15) в (8-16), получим:

(8-17)

Сравнение (8-14) с (8-17) показывает, что передаточная функция, определенная через матрицы, полностью совпадает с исходной.

Как и в классической теории автоматического управления можно и замкнутую систему охарактеризовать матричной передаточной функцией (рис.8.10).

В данной структуре на входе сравниваются две скалярные величины: - задающий сигнал;- сигнал обратной связи.

. (8-18)

Чтобы в результате произведения векторов получить скалярную величину, размерность векторов должна быть согласована -(),а-().

Подставляя значение из (8-18) в (8-14) получим соотношения, связывающие выходные координаты объекта с входными

Учитывая (8-15), определяем передаточную функцию замкнутой системы как отношение изображения выходного сигнала к изображению входного сигнала

. (8-19)

Результат можно проверить с помощью программы MatLab.

Пример 8.5.

%Запись lti объектов в различных подклассах

A=[0,1;-2,-3];B=[0;1];C=[1,0]; D=0; %Исходные данные.

h1=ss(A,B,C,D) %Представление данных в подклассе ss.

h2=tf(h1) %Преобразование данных от ss к tf.

Решение:

Llect_8_ex5

h1 =

a =

x1 x2

x1 0 1

x2 -2 -3

b =

u1

x1 0

x2 1

c =

x1 x2

y1 1 0

d =

u1

y1 0

8.6. Преобразование подобия. Системы регулирования с одним входом и одним выходом характеризуются внешними и внутренними характеристиками. Внешние характеристики однозначны. Это передаточные функции и дифференциальные уравнения. Количество внутренних характеристик (моделей состояния) неограниченно. В предыдущем параграфе по одной передаточной функции было получено три схемы моделирования, характеризующееся своими матрицами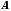, ,. В действительности для характеристики одной и той же системы можно предложить неограниченное количество матриц, ,, каждой из которых будет соответствовать модель в переменных состояния[7].Выбор той или иной модели зависит от конкретных обстоятельств:

- желание иметь в качестве переменных состояния естественные физические величины (скорость, положение, ток и т.д.), что позволяет перенести результаты моделирования на физическую модель без предварительных преобразований;

- желание облегчить синтез системы управления;

- желание формализовать процесс расчета.

Таким образом, существуют такие преобразования (преобразования подобия), которые изменяют внутреннюю структуру системы (модель состояния), но не изменяют соотношение между входом и выходом (передаточную функцию).

Преобразования подобия часто используются в современной теории управления, так как приходится определять различные характеристики систем в разных базисах. Поэтому рассмотрим преобразования подобия более подробно

(8-20)

Введем невырожденное линейное преобразование

, (8-21)

где -вектор состояния системы в новом базисе,- произвольная невырожденная матрица. Не вырожденность матрицы определяется ее рангом или определителем. Для невырожденной матрицы ранг должен быть равен степени характеристического уравнения, или её определитель не должен быть равен нулю. В пакетеMatLabне вырожденность матрицы определяется относительно просто соответствующими командами, что будет проиллюстрировано при расчетах систем регулирования.

Для перехода к новому базису умножим слева систему уравнений (8-20) на 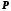, а затем значениеиз (8-21) подставим в систему (8-20):

В новых переменных уравнение системы принимает вид:

или