
- •Лекция_8. Модели в переменных состояния
- •8.2. Схемы моделирования
- •8.5. Определение матричных передаточных функций
- •Преобразованные матрицы новой системы координат вычисляются по формулам:
- •Преобразованные матрицы в новой системе координат имеют вид:
- •8.7. Команды MatLab в матричных преобразованиях
8.2. Схемы моделирования
Модель системы в переменных состояния можно получить двумя путями: - использую дифференциальные уравнения; - использую схемы моделирования.
Основным элементом схемы моделирования
является интегратор. Если выход
интегратора обозначит через
 ,
то его входом должна быть первая
производная
,
то его входом должна быть первая
производная .
Рассмотрим последовательное соединение
двух интеграторов рис.8.2.(а). Если выход
второго интегратора обозначит через
.
Рассмотрим последовательное соединение
двух интеграторов рис.8.2.(а). Если выход
второго интегратора обозначит через ,
то его входом должна быть первая
производная
,
то его входом должна быть первая
производная ;
аналогично входом первого интегратора
должна быть вторая
;
аналогично входом первого интегратора
должна быть вторая

производная. Цепочку из последовательно соединенных nинтеграторов можно использовать для моделирования системn порядка.
На рис.8.2.(б) представлена схема
моделирования механической системы.
Входом двух интеграторов является
вторая производная и уравнение механической системы (8-5)
принимает вид:
и уравнение механической системы (8-5)
принимает вид:
 .
(8-7)
.
(8-7)
Следовательно, чтобы связать все переменные, входящие в уравнение (8-7), схему рис.8.2.(а) нужно дополнить сумматором и тремя коэффициентами усиления. Общий принцип построения схем моделирования заключается в формировании структурной схемы, состоящей только из интеграторов, сумматоров и коэффициентов усиления.
Заметим, что если схема моделирования строится на основе дифференциальных уравнений, то структурная схема является однозначной, которая однозначно определяет все фазовые координаты системы. Если исходные данные представлены в виде передаточных функций, то схемы моделирования могут иметь разные структуры, которые приводят к неоднозначному представлению фазовых координат системы. Причем, многообразие представления фазовых координат системы не изменяет выходных сигналов этой системы.
По передаточным функциям системы можно представить множество схем моделирования. Наиболее часто схемы моделирования реализуются следующими способами:
- прямого программирования;
- параллельного программирования;
- последовательного программирования.
Для иллюстрации различных методов составления схем моделирования рассмотрим передаточную функцию
 .
.
Составим схему моделирования методом прямого программирования. Определим выходную величину, используя нижеприведенные обозначения
 ,
,
 .
.
При принятых обозначениях выходную
величину
 определяем следующим выражением
определяем следующим выражением
 .
(8-8)
.
(8-8)
Уравнение (8-8) разрешим относительно старшей производной и получим
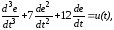

Составим схему моделирования по последнему уравнению (рис.8.3).
На основании схемы моделирования составим дифференциальные уравнения системы в переменных состояния. Предполагая, что входное воздействие является ступенчатой функцией, получим


Вектор состояния системы увеличенной размерности имеет вид
 .
.
Матрица коэффициентов
 увеличенной размерности, составленная
по схеме моделирования, запишется как
увеличенной размерности, составленная
по схеме моделирования, запишется как
 .
.
Как видно из схемы моделирования выходная
величина
 является линейной комбинацией переменных
состояния и составлена на основании
уравнения (8-8)
является линейной комбинацией переменных
состояния и составлена на основании
уравнения (8-8)
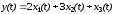 .
.
Матрицы коэффициентов системы, определенные по схеме моделирования, представлены ниже:
 .
.
Рассмотрим общий подход к построению схем моделирования методом прямого программирования.
Пусть передаточная функция системы имеет вид
 .Разделив
числитель и знаменатель
.Разделив
числитель и знаменатель на
на ,
получим
,
получим
 .
.
Выходная величина
 может быть выражена следующим образом
может быть выражена следующим образом

где
 .
.
Отсюда следует, что
 .
.
Из приведенных выражений ясно, что схема
переменных состояния должна содержать
nпоследовательно
включенных интегрирующих звеньев,
выходные величины которых соответственно
с коэффициентами ,
складываются с входным сигналом
,
складываются с входным сигналом и уменьшаются в
и уменьшаются в ,
образуя сигнал ошибки
,
образуя сигнал ошибки .
.
Далее сигнал
 ,
усиленный в
,
усиленный в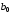 раз, суммируется с выходными величинами
интеграторов, взятыми с коэффициентами
раз, суммируется с выходными величинами
интеграторов, взятыми с коэффициентами образуя выходную величину
образуя выходную величину .
Полученная таким образом схема приведена
на рис.8.4.
.
Полученная таким образом схема приведена
на рис.8.4.

8.3.1 Параллельное программирование. Уравнение состояния системы можно получить из схемы моделирования, если предварительно разложить передаточную функцию на элементарные дроби. Для этого должны быть известны корни характеристического уравнения знаменателя

где
 корни характеристического уравнения
знаменателя передаточной функции
корни характеристического уравнения
знаменателя передаточной функции ,
коэффициенты
,
коэффициенты и
и определяются по формуле
определяются по формуле
 ,
,

Следует указать, что
 появится только тогда, когда степень
полинома числителя равна степени
полинома знаменателя, если полином
числителя имеет меньшую степень, то
появится только тогда, когда степень
полинома числителя равна степени
полинома знаменателя, если полином
числителя имеет меньшую степень, то ,
что выполняется для всех систем
регулирования, состоящих из инерционных
звеньев.
,
что выполняется для всех систем
регулирования, состоящих из инерционных
звеньев.
Применим эти положения к уже рассмотренному примеру
 .
.
Так как корни характеристического
уравнения знаменателя известны
 ,
,
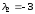 ,
, и коэффициенты
и коэффициенты ,
,
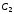 и
и определены
определены
 ,
,
 ,
, ;
;
то схема моделирования при параллельном программировании имеет вид (рис.8.5).

На основании схемы моделирования составим дифференциальные уравнения системы в переменных состояния для параллельного программирования. Предполагая, что входное воздействие является ступенчатой функцией, получим

Система уравнений определяет матрицу
коэффициентов

 .
.
Выход
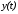 является, как и ранее, линейной комбинацией
координат
является, как и ранее, линейной комбинацией
координат ,
, и
и

Матрицы коэффициентов
 ,
,
 ,
, ,
, данной системы имеют вид:
данной системы имеют вид:
 .
.
На основании схемы моделирования запишем системы уравнений первого порядка
 ,
,
 .
.
Уравнения состояния для обычной не расширенной матрицы коэффициентов имеет вид
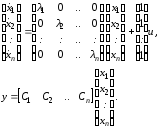
Описанный метод получения уравнений
состояния позволяет получить диагональную
матрицу, в которой используются в явной
форме собственные значения матрицы
(корни
 ),
что значительно упрощает последующие
выкладки. Если корни характеристического
уравнения комплексные, то выходные
сигналы соответствующих интеграторов
(фазовые координаты системы), будут
также комплексными, что затрудняет
физическую интерпретацию измеренных
координат состояния. Потому описанное
представление обычно не применяется,
если система регулирования имеет
комплексные корни.8.3.2.Последовательное
программирование. Для построения
схем в переменных состояния способом
последовательного программирования
передаточная функция должна быть
представлена в виде последовательного
соединения элементарных звеньев с
передаточными функциями вида
),
что значительно упрощает последующие
выкладки. Если корни характеристического
уравнения комплексные, то выходные
сигналы соответствующих интеграторов
(фазовые координаты системы), будут
также комплексными, что затрудняет
физическую интерпретацию измеренных
координат состояния. Потому описанное
представление обычно не применяется,
если система регулирования имеет
комплексные корни.8.3.2.Последовательное
программирование. Для построения
схем в переменных состояния способом
последовательного программирования
передаточная функция должна быть
представлена в виде последовательного
соединения элементарных звеньев с
передаточными функциями вида

Для каждой из этих передаточных функций на основе метода прямого программирования разработаны схемы в переменных состояния. Эти схемы представлены на рисунках 8.5(а)-8.5(з).







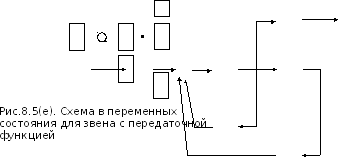


Структурные схемы моделирования передаточных функций, образованных полиномами первой и второй степени, изображены на рис.8.6.

На рис.8.7.представлены схемы моделирования передаточных функций, образованных полиномами второй степени.

Например, для передаточной функции
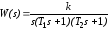 .
(8-9)
.
(8-9)
схема моделирования, полученная методом последовательного программирования, изображена на рис.8.8.

Схема в переменных состояния (рис.8.9) получена из передаточной функции
 ,
(8-10)
,
(8-10)
если её предварительно представить в виде произведения элементарных звеньев
 ,
,
а затем, пользуясь справочной литературой, каждому из элементарных звеньев поставить в соответствие схему моделирования.

Система дифференциальных уравнений первого порядка, записанная на основании схемы рис.8.9 имеет вид

Расширенная матрица коэффициентов при ступенчатом воздействии, представлена ниже
 .
.
Выход
 определяется линейной комбинацией
фазовых координат
определяется линейной комбинацией
фазовых координат
 .
.
Матрицы коэффициентов
 ,
,
 ,
, ,
, данной системы представлены ниже:
данной системы представлены ниже:
 .
.
Выбор способа построения схемы переменных
состояния в каждом конкретном случае
определяется сложностью передаточной
функции системы, а также требованиям,
предъявляемым к расчету системы.
Например, способ прямого программирования
целесообразно применять в тех случаях,
когда передаточная функция системы
имеет высокий порядок и разложение на
элементарные дроби затруднено. Когда
же необходимо определить не только
выходную величину, но и другие переменные
(скорость, ток и т.д.), которые соответствуют
переменным физической системы, то
целесообразно применять способ
последовательного программирования.
При этом способе моделирования фазовые
координаты модели и физически реализуемой
системы совпадают. При теоретических
исследованиях целесообразно применять
метод параллельного программирования.
В этом случае матрица принимает наиболее
простой (диагональный) вид, так как все
координаты развязаны. Следует отметить,
что при комплексных корнях системы
регулирования в матрице коэффициентов
 и в матрице управления
и в матрице управления появятся комплексные числа, что затрудняет
применение метода параллельного
программирования.
появятся комплексные числа, что затрудняет
применение метода параллельного
программирования.
8.4. Методы решения уравнений состояния.Уравнения состояния могут быть заданы либо дифференциальными уравнениями, либо передаточными функциями. В зависимости от этого предложено два метода решения [7].
Определим выходной сигнал системы, используя преобразование Лапласа. Для этого матричную запись уравнений состояния

представим в виде системы уравнений. Рассмотрим первое из этих уравнений.
 ,
,
где
 и
и - соответствующие элементы матриц
- соответствующие элементы матриц и
и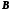 .
Преобразуя это уравнение по Лапласу,
получим
.
Преобразуя это уравнение по Лапласу,
получим
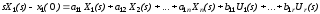 ,
,
где учтено начальное условие, т.к. нам необходимо найти полное решение. Преобразуем по Лапласу второе уравнение системы
 .
.
Преобразуем по Лапласу остальные уравнения системы и тогда получим окончательный результат в матричной форме
 ,
,
где
 .
.
Для решения матричного уравнения
сгруппируем все члены, содержащие
 ,
в левой части
,
в левой части
 .
.
Теперь необходимо выделить множитель
 .
Для этого введем единичную матрицу.
.
Для этого введем единичную матрицу.
 . (8-11)
. (8-11)
Этот дополнительный шаг понадобился
потому, что вычитание матрицы
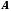 из скалярной переменной не определено.
Из уравнения (8-11) получаем
из скалярной переменной не определено.
Из уравнения (8-11) получаем
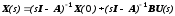 .
.
Тогда вектор состояния
 будет обратным преобразованием Лапласа
от
будет обратным преобразованием Лапласа
от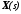 .
.
Общее решение матричного уравнения
определятся через фундаментальную
матрицу
 :
:
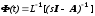 . (8-12)
. (8-12)
Заметим, что для системы n-го
порядка фундаментальная матрица имеет
размерность( ).
Обратное преобразование Лапласа для
матрицы определяется путем применения
обратного преобразования к каждому
элементу этой матрицы. Определение
фундаментальной матрицы по выражению
(8-12) требует значительных затрат и
сопряжено с возможными ошибками.
Проиллюстрируем эти положения на
конкретном примере.
).
Обратное преобразование Лапласа для
матрицы определяется путем применения
обратного преобразования к каждому
элементу этой матрицы. Определение
фундаментальной матрицы по выражению
(8-12) требует значительных затрат и
сопряжено с возможными ошибками.
Проиллюстрируем эти положения на
конкретном примере.
Пример 8.2.
Задана передаточная функция
 .
(8-13)
.
(8-13)
По передаточной функции запишем уравнения состояния системы
 ,
,
 .
.
Для определения фундаментальной матрицы
сначала найдем матрицу ( )
)
 .
.
Чтобы определить фундаментальную матрицу, сформируем присоединенную матрицу
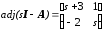 ,
,
и вычислим определитель
 .
.
Тогда обратная матрица будет получена путем деления присоединенной матрицы на определитель
 .
.
Фундаментальную матрицу получим с помощью обратного преобразования Лапласа
 .
.
Программа MatLab позволяет выполнить эти преобразования более экономно
Пример 8.3.
%Определение фундаментальной матрицы
h=tf(1,[1,3,2]); %Ввод исходных данных в форме tf.
h1=ss(h); %Преобразование данных от формы tf форме ss.
h2=canon(h1,'companion'); %Переход к канонической форме ИКП
h3=h2' %Транспонирование матриц
A=[0,1;-2,-3]; %Численные значения матрицы перенесено
%из командного окна MatLab
syms s t %Ввод символьных переменных
I=[s,0;0,s]; %Ввод единичной матрицы
V=ilaplace(inv(I-A)) %Определение фундаментальной матрицы
%Программа MatLab для символьного
%решения матричных уравнений
S=dsolve('Dx1=x2,Dx2=-2*x1-3*x2,x1(0)=0,x2(0)=0','x')
Решение : %Определение фундаментальной матрицы
h=tf(1,[1,3,2]); %Ввод исходных данных в форме tf.
h1=ss(h); %Преобразование данных от формы tf форме ss.
h2=canon(h1,'companion'); %Переход к канонической форме ИКП
h3=h2' %Транспонирование матриц
A=[0,1;-2,-3]; %Численные значения матрицы перенесено
%из командного окна MatLab
syms s t %Ввод символьных переменных
I=[s,0;0,s]; %Ввод единичной матрицы
V=ilaplace(inv(I-A)) %Определение фундаментальной матрицы
%Программа MatLab для символьного
%решения матричных уравнений
S=dsolve('Dx1=x2,Dx2=-2*x1-3*x2,x1(0)=0,x2(0)=0','x')
Результат решения:
>> Llect_8
h3 =
a =
x1 x2
x1 0 -1
x2 2 3
b =
u1
x1 0
x2 -1
c =
x1 x2
y1 1 0
d =
u1
y1 0
Continuous-time state-space model.
V =
[ 2*exp(-t) - exp(-2*t), exp(-t) - exp(-2*t)]
[ 2*exp(-2*t) - 2*exp(-t), 2*exp(-2*t) - exp(-t)]
S =
x2: [1x1 sym]
x1: [1x1 sym]
