
- •Лекция_8. Модели в переменных состояния
- •8.2. Схемы моделирования
- •8.5. Определение матричных передаточных функций
- •Преобразованные матрицы новой системы координат вычисляются по формулам:
- •Преобразованные матрицы в новой системе координат имеют вид:
- •8.7. Команды MatLab в матричных преобразованиях
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Лекция_8. Модели в переменных состояния

Владимир Куш
Содержание.
8.1.Представление моделей в векторно-матричной форме
8.2. Схемы моделирования
8.3. Методы решения уравнений состояния
8.3.1 Параллельное программирование
8.3.2.Последовательное программирование
8.4. Методы решения уравнений состояния
8.5. Определение матричных передаточных функций
8.6. Преобразование подобия
8.7. Команды MatLab в матричных преобразованиях
ЭССЕ. Описаны методики составления управления линейных систем в пространстве состояния на основе дифференциальных управлений, передаточных функций и схем моделирования. Введены понятия базиса. В пакете MatLab приведены команды и программы, позволяющие исследовать системы в разных базисах. Цель – уметь в пакете Control System Toolbox по схеме моделирования или передаточной функции написать программу, используя разные базисы, для исследования систем регулирования.
8.1.Представление моделей в векторно-матричной форме
Рассмотрим пример, иллюстрирующий
составление уравнений в переменных
состояния. На рис. 8.1 изображена
механическая система с линейным
перемещением
 .
На тело массой
.
На тело массой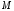 действует три силы – внешняя сила
действует три силы – внешняя сила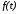 ,
сила трения, пропорциональная скорости,
–
,
сила трения, пропорциональная скорости,
– ,
сила упругости, пропорциональная
перемещению, –
,
сила упругости, пропорциональная
перемещению, – .
Под действием этих сил тело массой
.
Под действием этих сил тело массой движется согласно закона Ньютона,
который гласит, что сумма сил, действующих
на тело, равна произведению массы тела
на его ускорение.
движется согласно закона Ньютона,
который гласит, что сумма сил, действующих
на тело, равна произведению массы тела
на его ускорение.
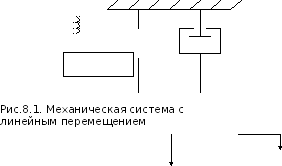
связывающее движение системы, имеет вид:
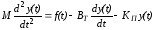 ,
(8-1)
,
(8-1)
а передаточная функция равна
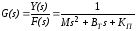 .
(8-2)
.
(8-2)
Это выражение определяет зависимость
положения
 от действующей силы
от действующей силы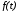 .Допустим, что нам нужна также информация
о скорости. Тогда, используя метод
переменных состояния, мы введём следующие
переменные:
.Допустим, что нам нужна также информация
о скорости. Тогда, используя метод
переменных состояния, мы введём следующие
переменные:

и
 .
(8-3)
.
(8-3)
Здесь
 есть положение массы, а
есть положение массы, а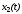 - ее скорость. На основании (8-1) и (8-2) можно
записать:
- ее скорость. На основании (8-1) и (8-2) можно
записать:
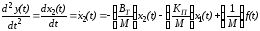 .
(8-4)
.
(8-4)
Уравнения (8-3) и (8-4) описывают перемещение массы, которое является системой дифференциальных уравнений первого порядка:
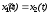 ,
,
 ,
(8-5)
,
(8-5)
 .
.
Представим систему уравнений (8-5) в векторно-матричной форме, что позволяет привлечь аппарат векторно-матричной алгебры к расчету систем регулирования.
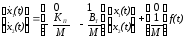 ,
,
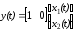 .
.
Теперь ответим на вопрос: что же будем понимать под состоянием системы?
Определение.Состояние системы в
любой момент времени – это количество
информации, которое вместе со всеми
входными переменными однозначно
определяет поведение системы при всех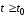 .
.
Ниже будет показано, что вектор состояния, полученный на основании дифференциальных уравнений системы, удовлетворяет этому определению.
Стандартная форма уравнения линейной стационарной непрерывной системы имеет вид:
 ,
(8-6)
,
(8-6)
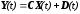 ,
,
где вектор
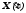 есть производная по времени от вектора
есть производная по времени от вектора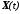 .
.
В этих уравнениях
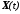 - вектор состояния размерности(
- вектор состояния размерности( ),
компонентами которого являются переменные
состояния системыn-го
порядка;
),
компонентами которого являются переменные
состояния системыn-го
порядка;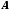 - матрица коэффициентов системы(
- матрица коэффициентов системы(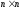 );
);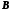 - матрица входа(
- матрица входа( );
);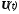 - вектор входа размерности(
- вектор входа размерности(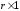 ),
компонентами которого являются входные
переменные системы;
),
компонентами которого являются входные
переменные системы; - вектор входа размерности(
- вектор входа размерности(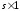 ),
компонентами которого являются выходные
переменные системы;
),
компонентами которого являются выходные
переменные системы; - матрица выхода(
- матрица выхода(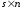 );
);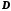 - матрица обхода, определяющая прямую
зависимость выхода от входа.
- матрица обхода, определяющая прямую
зависимость выхода от входа.
Вектор
 ,
в частном, но часто встречающимся случае
может быть скаляром, что описыват
поведение одномерной системы.
Преобразование векторной величины в
скалярную достигается умножением
вектора строки
,
в частном, но часто встречающимся случае
может быть скаляром, что описыват
поведение одномерной системы.
Преобразование векторной величины в
скалярную достигается умножением
вектора строки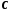
 на вектор столбец
на вектор столбец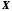
 .
Поэтому при обозначениях выходных
координат системы могут использоваться
как скалярные, так и векторные обозначения.
.
Поэтому при обозначениях выходных
координат системы могут использоваться
как скалярные, так и векторные обозначения.
Все векторы (сигналы) можно представить в развернутом виде:
 ;
; ;
;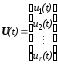 ;
;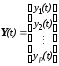 .
.
В приведенных записях уравнений приняты следующие обозначения: вектора матрицы записаны полужирными наклонными заглавными буквами, а их составляющие - прописными.
Вернемся к уравнению (8-6). Первое из них
есть матричное дифференциальное
уравнение первого порядка. Оно называется
уравнением «вход-состояние», а его
решением является вектор состояния
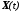 .
Второе уравнение называется уравнением
«вход-состояние-выход», которое позволяет
определить вектор выхода
.
Второе уравнение называется уравнением
«вход-состояние-выход», которое позволяет
определить вектор выхода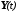 по известным вектору входа
по известным вектору входа и вектору состояния
и вектору состояния .
Матрица
.
Матрица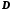 в силовых системах регулирования обычно
равна нулю, т.к. системы регулирования
являются усилителями мощности и мощность
на выходе значительно больше мощности
входе. При расчетах фильтров мощности
на входе и выходе соизмеримы, и матрица
в силовых системах регулирования обычно
равна нулю, т.к. системы регулирования
являются усилителями мощности и мощность
на выходе значительно больше мощности
входе. При расчетах фильтров мощности
на входе и выходе соизмеримы, и матрица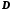 может иметь значение отличное от нуля.
Это еще раз подчеркивает универсальность
метода пространства состояния, который
применим к расчету силовых систем и
фильтров.
может иметь значение отличное от нуля.
Это еще раз подчеркивает универсальность
метода пространства состояния, который
применим к расчету силовых систем и
фильтров.
Левая часть дифференциальных уравнений
относительно
 всегда представлена только первыми
производными переменных состояния,
правая же часть не должна содержать
никаких производных. В уравнении
относительно выхода
всегда представлена только первыми
производными переменных состояния,
правая же часть не должна содержать
никаких производных. В уравнении
относительно выхода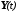 также не должно быть никаких производных.
Разумеется, систему можно описать
уравнениями, в которых эти правила не
соблюдаются, но эти уравнения уже не
будут иметь стандартную форму.
также не должно быть никаких производных.
Разумеется, систему можно описать
уравнениями, в которых эти правила не
соблюдаются, но эти уравнения уже не
будут иметь стандартную форму.
Уравнения состояния (8-6) записаны в
предположении, что у системы имеется
несколько входных и выходных переменных.
Такие системы принято называть
многомерной. Если у системы
имеется только один вход, то матрица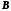 имеет вид столбца, а вектор
имеет вид столбца, а вектор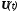 превращается в скалярную переменную.
Если у системы только один выход, то
вектор
превращается в скалярную переменную.
Если у системы только один выход, то
вектор превращается в скалярную переменную,
а матрицаCпринимает вид
строки. Ниже приводится пример составления
уравнений состояния для многомерной
системы.
превращается в скалярную переменную,
а матрицаCпринимает вид
строки. Ниже приводится пример составления
уравнений состояния для многомерной
системы.
Пример 8.1.
Рассмотрим систему, описываемую дифференциальными уравнениями:
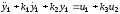 ,
,
 .
.
где
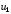 и
и - входные переменные, а
- входные переменные, а
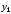 и
и
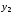 - выходные переменные. Зависимость
переменных от времени для удобства
опущена. За переменные состояния мы
можем принять выходы системы и, если
понадобится, их производные:
- выходные переменные. Зависимость
переменных от времени для удобства
опущена. За переменные состояния мы
можем принять выходы системы и, если
понадобится, их производные:
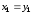 ;
; ;
; .
.
Тогда исходную систему уравнений можно представить в виде:
 ,
,
 .
.
Окончательно уравнения принимают вид:
 ,
,
 ,
,
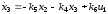 .
.
К ним добавляются уравнения для выходных переменных:
 ,
,
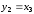 .
.
Эти уравнения можно записать в векторно-матричной форме:
 ,
,
 .
.
Представим, что уравнения, приведенные
в рассмотренном примере, представляют
собой модель механической системы с
линейным перемещением. Допустим, далее,
что
 и
и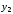 - это текущее положение некоторых
элементов системы. Тогда
- это текущее положение некоторых
элементов системы. Тогда есть скорость движения системы.
Следовательно, все переменные состояния
соответствуют реальным физическим
переменным системы:
есть скорость движения системы.
Следовательно, все переменные состояния
соответствуют реальным физическим
переменным системы: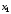 и
и - это перемещения, а
- это перемещения, а - скорость. Вообще говоря, желательно
(но не обязательно), чтобы в качестве
переменных состояния выступали реальные
физические переменные. Далее рассмотрим
метод получения уравнений состояния
непосредственно по передаточной функции
системы. В общем случае переменные
состояния, получаемые таким способом,
могут не соответствовать реальным
физическим переменным.
- скорость. Вообще говоря, желательно
(но не обязательно), чтобы в качестве
переменных состояния выступали реальные
физические переменные. Далее рассмотрим
метод получения уравнений состояния
непосредственно по передаточной функции
системы. В общем случае переменные
состояния, получаемые таким способом,
могут не соответствовать реальным
физическим переменным.
