Определение координат вектора в данном базисе

Пусть мы имеем два вектора и вектор . Если , то .

Если же в пространстве имеем n векторов, то разложение любого вектора можно записать в виде системы «n» линейных уравнений с «n» переменными.

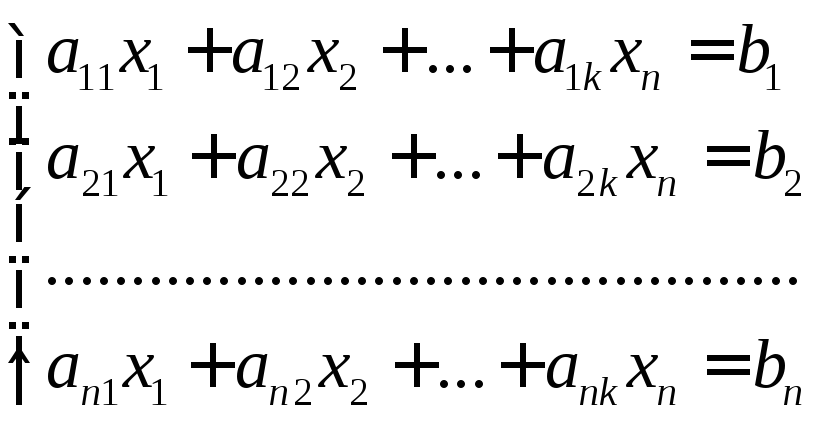(4)

Компоненты вектора образуют столбец при переменной x_i в данной системе.

Если определитель этой системы 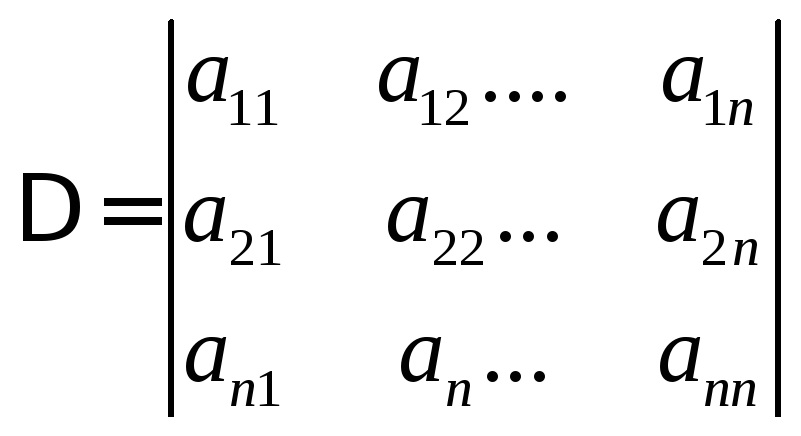отличен от нуля , то система имеет единственное решение и векторы образуют базис пространства.

А вектор разлагается по этому базису в виде .

Например. Даны векторы в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Составляем определитель из векторов

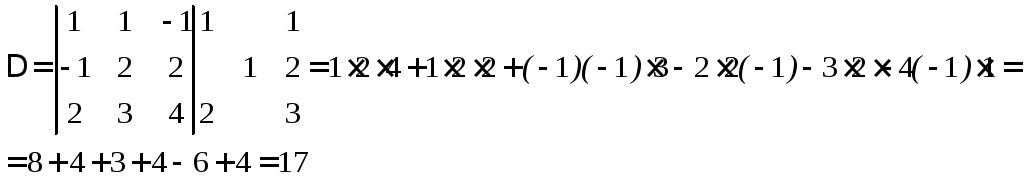
Т.к. , то векторы линейно независимы и образуют базис в пространстве . Находим координаты вектора в этом пространстве. Составляем систему 3-х уравнений

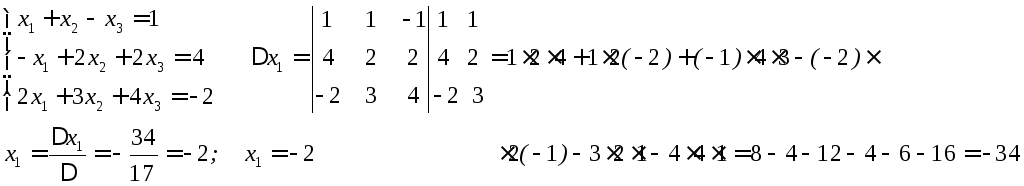
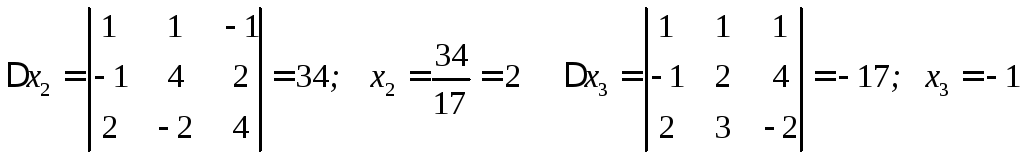
Таким образом, получаем

.

Системы координат и скалярное произведение векторов Декартова система координат

Фиксируем в пространстве точку О и рассмотрим произвольную точку М.

называют радиус-вектор точки М. Если в пространстве кроме точки О выбран базис, то точке М можно сопоставить упорядоченную тройку чисел – компоненты ее радиус-вектора. Декартовой системой координат называют совокупность точки и базиса.

Точка О называется началом координат, а прямые проходящие через нее в направлении базисных векторов, называются осями координат. Первая – осью абсцисс, а вторая – осью ординат, третья осью – аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.

Компоненты радиуса вектора точки М по отношению к началу координат, называются координатами точки М. Соответственно первая координата – абсциссой, вторая - ординатой, третья – аппликатой.

К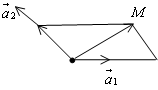оординаты точки пишут в скобках М (1; 2; -1). Если на плоскости, то М (1; 2).

Р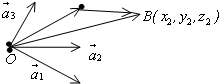ассмотрим две точки А и В, относительно декартовой системы координат , и . Очевидно, что . Вектор имеет следующие компоненты .

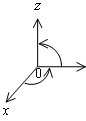
Рассмотрим пространственную систему координат с взаимно перпендикулярными осями x, y , z.

Е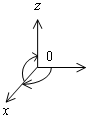е называют прямоугольной. Если поворот от к и (глядя c поло-

жительного направления z) происходит вправо, то такая система координат

называется правой, а если влево, то ее называют левой. В дальнейшем мы

б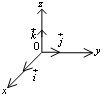удем использовать в основном правую систему координат. Единичные векторы по направлению осейx, y, z называются соответственно . В дальнейшем для

удобства стрелки будем ставить только на ортах . Базис с такими ортами называется ортонормированным. Декартовой прямоугольной системой координат называют систему координат с ортонормированным базисом координаты точки со знаком + или – относительно декартовой прямоугольной системы по абсолютной

величине равны расстояниям от этой точки до соответствующих координатных плоскостей.

Полярная система координат

П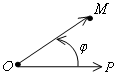усть задана точка О, называемая полюсом и исходящая из него ось ОР, которая называется полярной осью. Длину вектора называют полярным радиусом, а угол .φ – полярным углом. Последний определен с точностью до 2πk. Обозначаются полярные координаты M (r, φ).

Н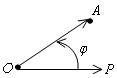апример . Если r = 0, то точка М совпадает с полюсом.

Скалярное произведение векторов.

С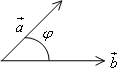калярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

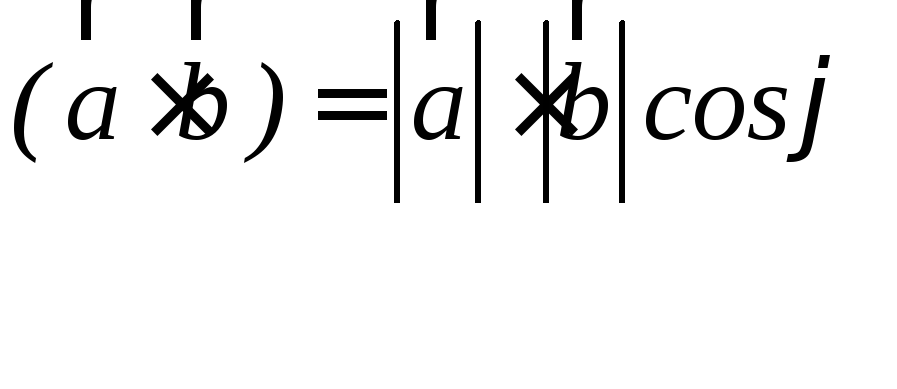
С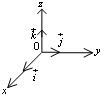калярное произведение равно нулю, если один из векторов равен нулю либо (т.е. сомножители ортогональны). Векторы ортонормированного базиса удовлетворяют соотношениям 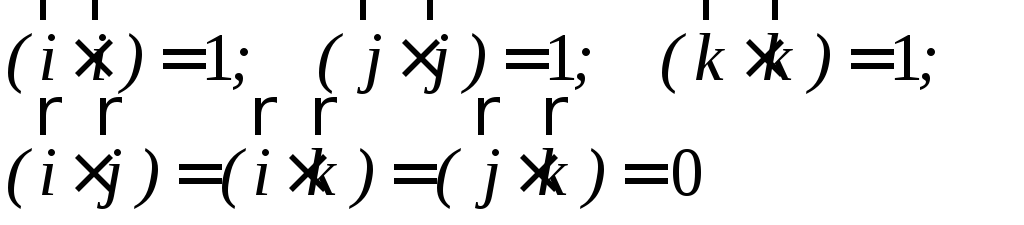Для любого .

Если единичные орты, то - координаты вектора

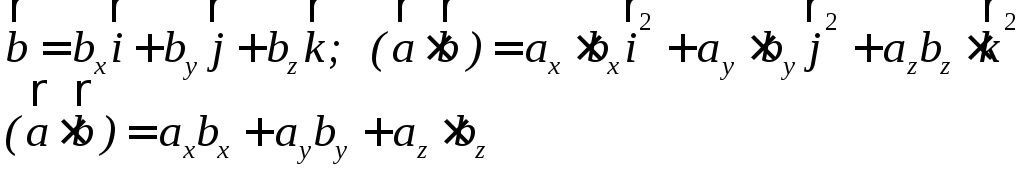
Например:

.

Длина вектора будет

Например, вычислить , если .

.

При этом угол между векторами будет φ будет

.

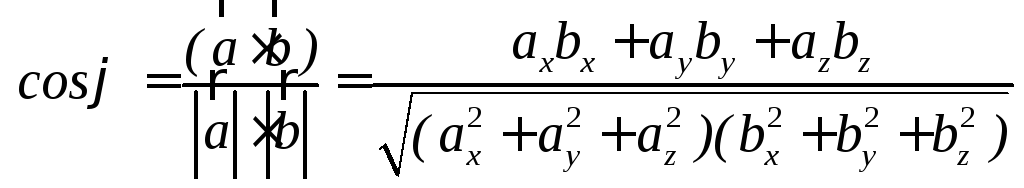Например

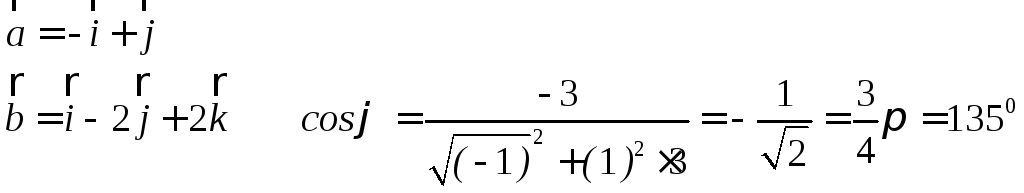
Векторное произведение двух векторов

Векторным произведением двух векторов и есть вектор , определяемый следующим образом

1. Модуль вектора 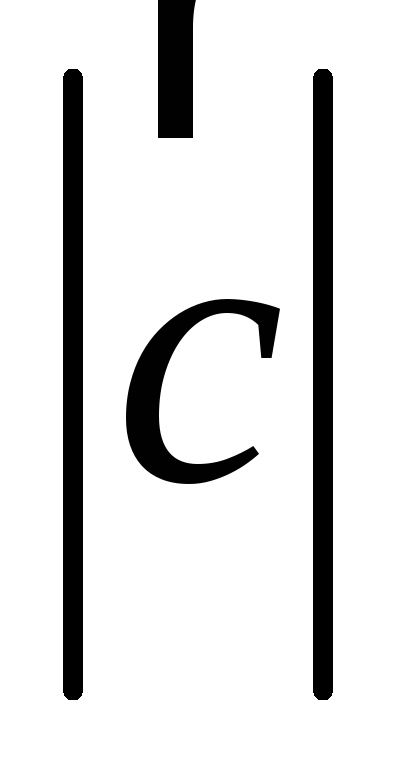равен площади параллелограмма.

2. Вектор 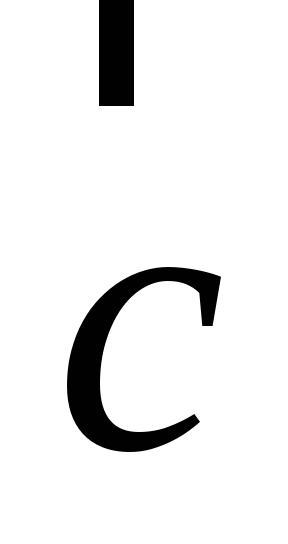перпендикулярен к векторам и .

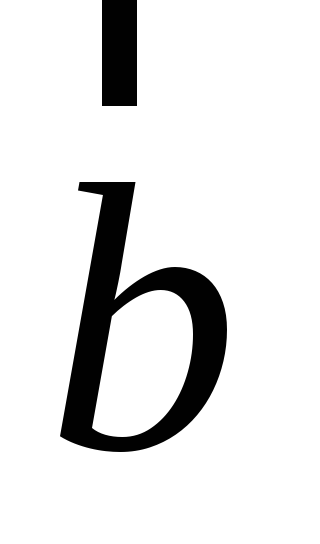3. Направление вектора 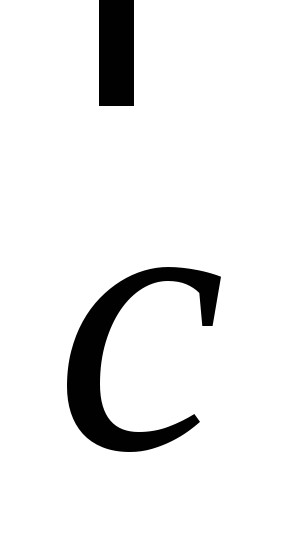такое, чтобы с его конца видеть поворот от к против часовой стрелки.

Если один из векторов или угол φ будет равным нулю, то и векторное произведение также равно нулю.

Свойства векторного произведения

а) , т.е. векторное произведение не обладает переместительным (коммутативным) законом

б) , т.е. соблюдается сочетательный (ассоциативный) закон.

в) соблюдается распределительный (дистрибутивный) закон.

Н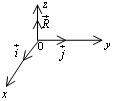айдем теперь произведения координатных ортов

.

Теперь найдем , если они выражены через проекции

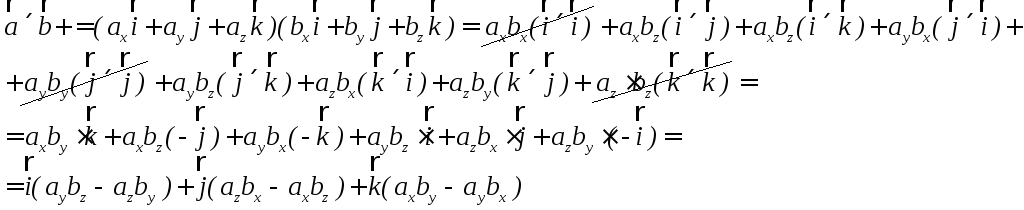
Это можно представить в виде 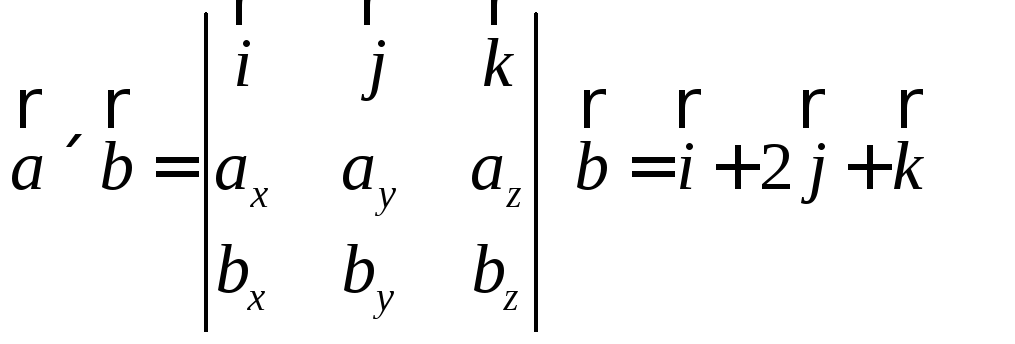. Например, найти , если