
- •Высшая математика конспект лекций
- •1 Курс, 1 семестр
- •Содержание
- •Тема 1 «Элементы линейной алгебры» 7
- •Тема 2 «Элементы векторной алгебры» 22
- •Тема 3 «Элементы аналитической геометрии» 30
- •Тема 4 «Введение в анализ» 51
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» 66
- •Введение
- •Тематический план
- •§ 2. Определители 3-го порядка
- •§ 3. Миноры и алгебраические дополнения
- •§ 1. Определители высших порядков.
- •Система двух уравнений с двумя неизвестными
- •Система 3-х уравнений первой степени с 3-мя неизвестными
- •Понятие о матрицах
- •Сложение матриц и умножение их на число
- •Транспонирование матриц
- •Перемножение матриц
- •Решение систем линейных уравнений методом Гаусса
- •Решение систем 3-х уравнений с 3-мя неизвестными с помощью формул Крамера
- •Исследование систем линейных уравнений
- •§ 1. Общие понятия. Систему уравнений вида
- •§ 2. Система 2-х уравнений с 2-мя неизвестными
- •§ 3. Система 3-х уравнений с 3-мя неизвестными
- •Вопросы для самоконтроля
- •Тема 2 «Элементы векторной алгебры» Основные понятия
- •Линейные операции над векторами
- •Линейная зависимость и независимость векторов
- •Определение координат вектора в данном базисе
- •Системы координат и скалярное произведение векторов Декартова система координат
- •Полярная система координат
- •Скалярное произведение векторов.
- •Векторно-скалярное (смешанное) произведение
- •§ 1. Вычисление объема параллелепипеда
- •§3.Направляющие косинусы
- •Вопросы для самоконтроля
- •Тема 3 «Элементы аналитической геометрии»
- •П 4. Переход от полярных координат к декартовым и обратно
- •Простейшие задачи аналитической геометрии на плоскости п 1. Проекция отрезка на оси координат
- •П 2 .Расстояние между двумя точками на координатной плоскости
- •П 3. Деление отрезка в данном отношении
- •Линии и их уравнения п 1. Понятие уравнения линии
- •П 2. Примеры заданий линий при помощи уравнений
- •П 3. Получение линии как геометрического места точек
- •П 4. Параметрические уравнения линий
- •П 5. Алгебраические линии
- •Прямая на плоскости п 1. Угловой коэффициент
- •П 3. Уравнение прямой, проходящей через данную точку м1 (х1; у1)
- •П 8. Уравнение прямой в отрезках
- •П 9. Нормальное уравнение прямой
- •П. 10. Расстояние от точки до прямой
- •П. 11. Уравнение прямой в полярных координатах
- •П. 3 Эллипс и его каноническое уравнение
- •П.4 Эксцентриситет и директрисы эллипса
- •Гипербола и ее каноническое уравнение
- •П 6. Асимптоты гиперболы
- •П 7. Эксцентриситет и директрисы гиперболы
- •П. 8 Парабола и ее уравнение
- •П. 9 Уравнение эллипса, гиперболы и параболы в полярных координатах
- •Преобразование координат п. 1 Преобразование координат при параллельном сдвиге осей
- •П 3. Преобразование декартовых координат при изменении начала и поворота осей
- •П. 4 Преобразование общего уравнения второй степени не содержащего произведения переменных
- •П 5. Преобразование общего уравнения второго порядка
- •Аналитическая геометрия в пространстве Уравнение прямой
- •Понятие об уравнении плоскости.
- •Уравнения поверхностей
- •Вопросы для самоконтроля
- •Тема 4 «Введение в анализ» Переменные и постоянные величины. Понятие функции.
- •Основные характеристики функций.
- •Основные элементарные функции и их графики.
- •Числовая последовательность.
- •Предел функции.
- •Бесконечно малые величины.
- •Бесконечно большие функции.
- •Соотношение между бесконечно малыми и бесконечно большими функциями.
- •Основные теоремы о пределах.
- •Типы неопределенностей и способы их раскрытия.
- •Первый замечательный предел.
- •Эквивалентные бесконечно малые и основные теоремы о них.
- •Непрерывность функций.
- •Основные теоремы о непрерывных функциях.
- •Вопросы для самоконтроля
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» Определение производной.
- •Геометрический смысл производной.
- •Производные основных элементарных функций.
- •Производная сложной и обратной функции.
- •Дифференцирование неявно заданной функции.
- •Дифференцирование функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Производные высших порядков.
- •Производные высших порядков неявно заданной функции.
- •Производные высших порядков от функций заданных параметрически.
- •Дифференциал функции.
- •Правила вычисления дифференциала.
- •Приложения производной.
- •Исследование функций при помощи производной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Вопросы для самоконтроля
- •Литература
Исследование систем линейных уравнений
§ 1. Общие понятия. Систему уравнений вида
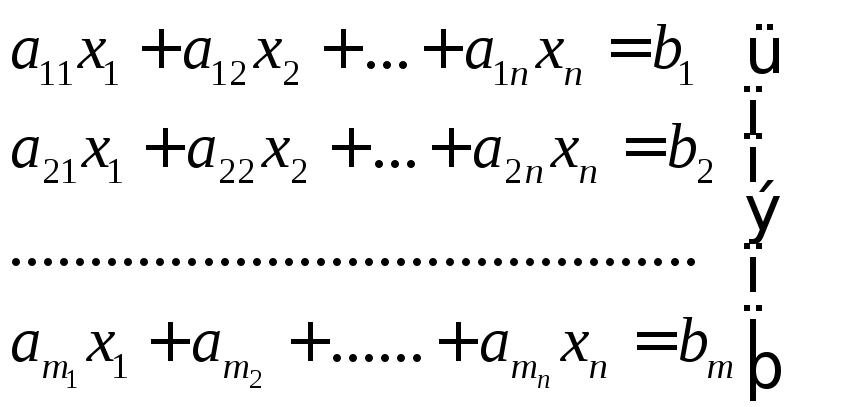 (1)
(1)
называют системой «m» линейных уравнений с «n» неизвестными x1, x2, ……xn все остальные величины известны. Числа, стоящие в правых частях уравнений, называют свободными членами. Если свободные члены всех уравнений равны нулю, то система называется однородной и наоборот.
Совокупность «n» чисел α1, α2,…… αn называется решением системы (1), если каждое уравнение системы обращается в числовое равенство после подстановки в него αi вместо соответствующих неизвестных xi .
При
этом могут представиться различные
случаи: а) система имеет единственное
решение, например
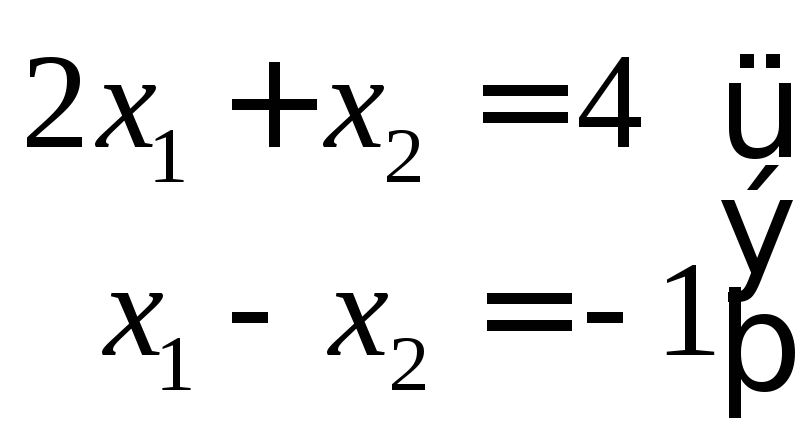
б) система может вообще не иметь решений
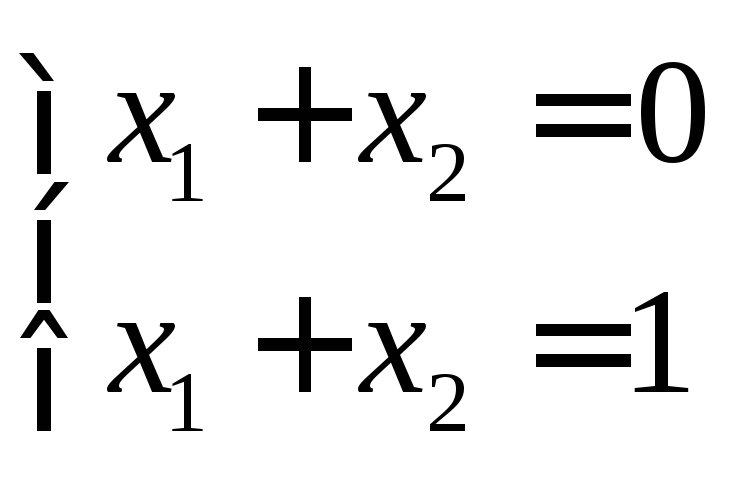 Если
такие системы не имеют смысла, то их
называют несовместными,
а имеющие решения – совместными
Если
такие системы не имеют смысла, то их
называют несовместными,
а имеющие решения – совместными
в) система имеет множество решений (обычно если n > m), т.е. когда количество неизвестныx больше количества уравнений х1 + х2 = 0
§ 2. Система 2-х уравнений с 2-мя неизвестными
Рассмотрим неоднородную систему
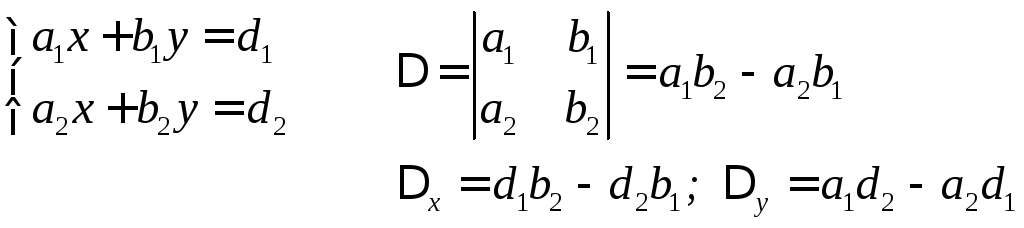
Если
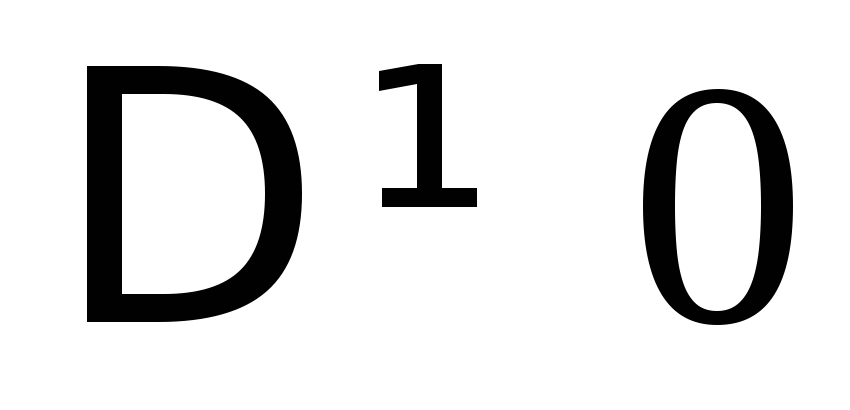 ,
то и
,
то и
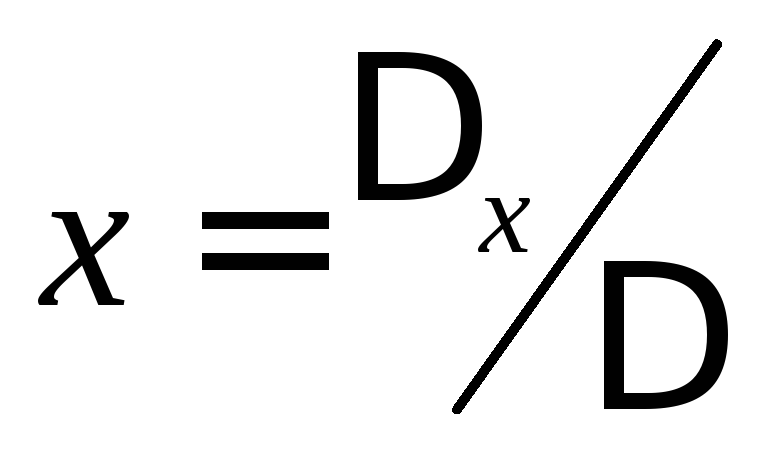
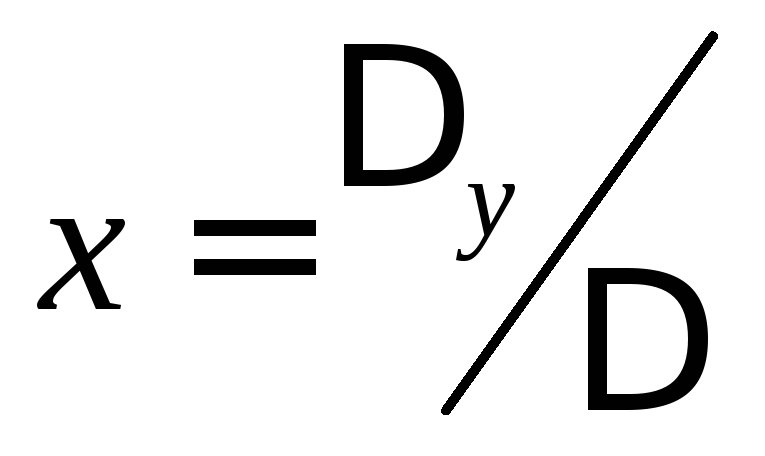 ,
т.е. система имеет единственное решение.
,
т.е. система имеет единственное решение.Если
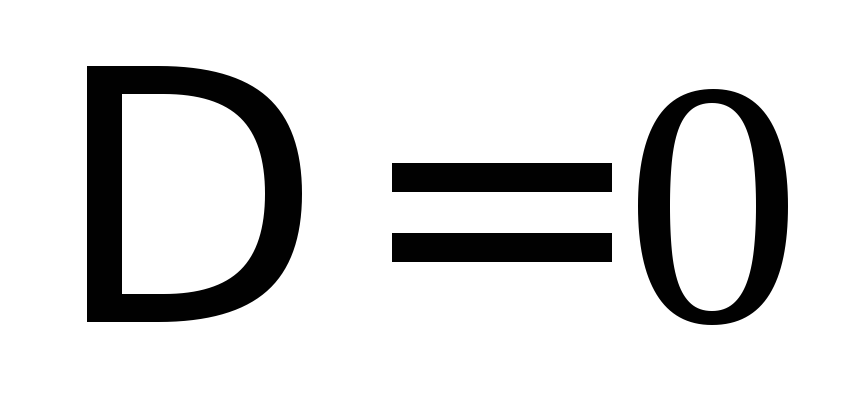 ,
то
,
то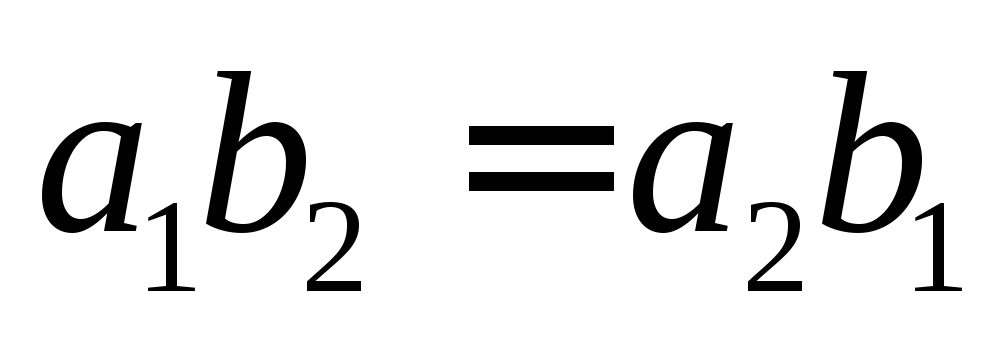 ,
т.е.
,
т.е.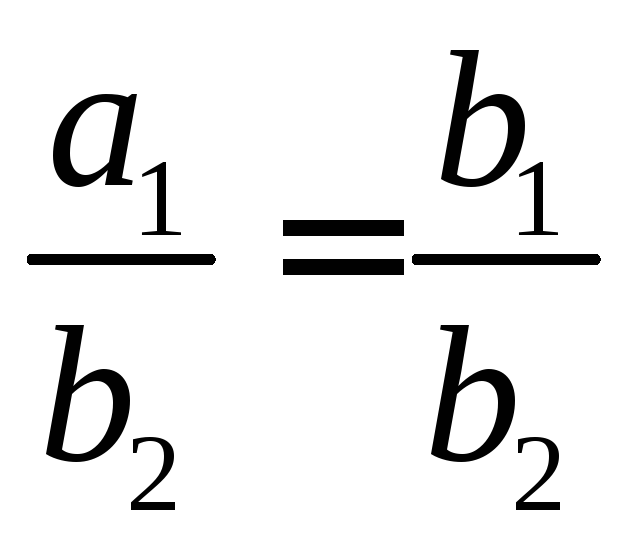
Здесь могут быть два случая
а)
![]() или
или
![]() или оба определителя не равны нулю.
или оба определителя не равны нулю.
Пусть
![]() = 0,
= 0,
![]() .
Т.е.
.
Т.е.
![]() .
Поэтому
.
Поэтому
![]()
![]() .
.
Следовательно,
система не совместна. Пример
![]()
б)
оба определителя
![]() равны нулю.
равны нулю.
![]() .
.
Последнее уравнение есть следствие предыдущих, поэтому эта система имеет бесконечное множество решений, т.е. неопределенна.
Например:
![]()
Здесь
второе уравнение есть следствие первого
![]() ,
которое имеет множество решений.
,
которое имеет множество решений.
Однородные системы
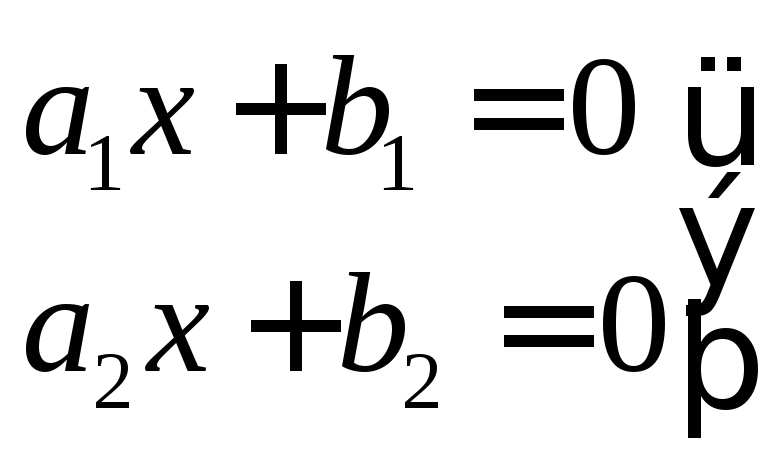 Здесь
Здесь
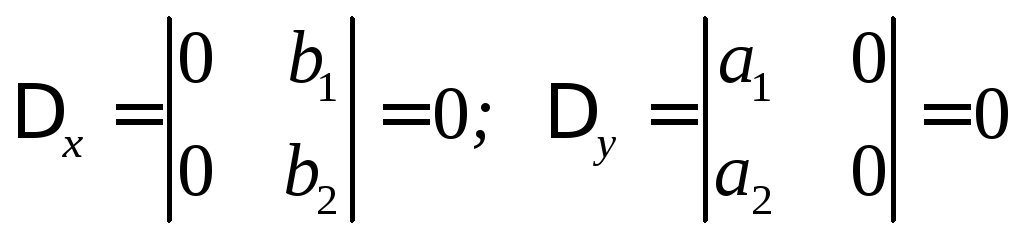 и все зависит от определителя
и все зависит от определителя
![]() .
.
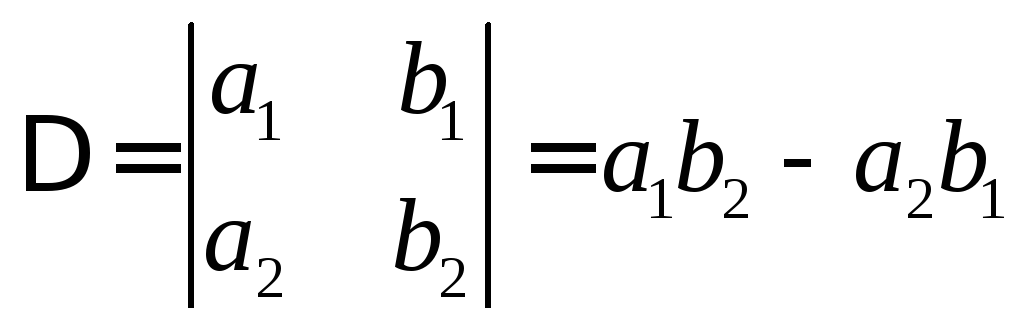 ;
имеем 2 случая
;
имеем 2 случая
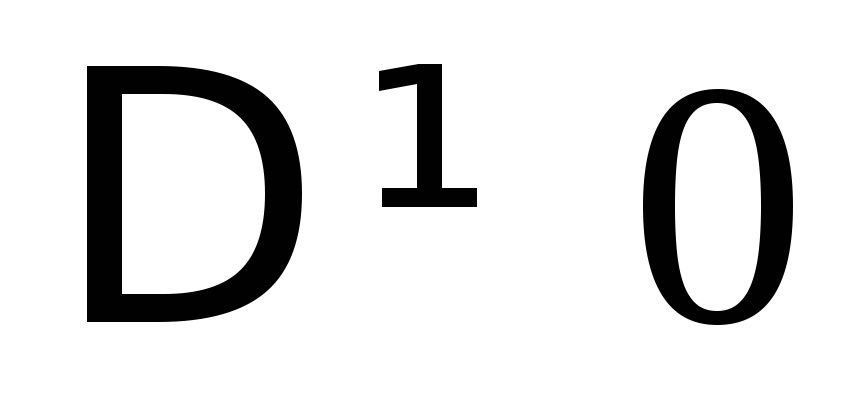 .
Тогда
.
Тогда
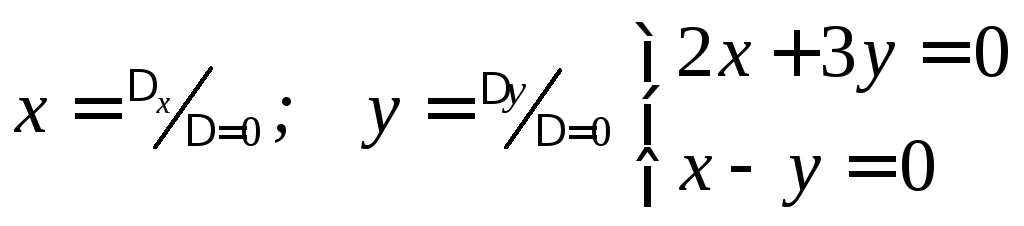
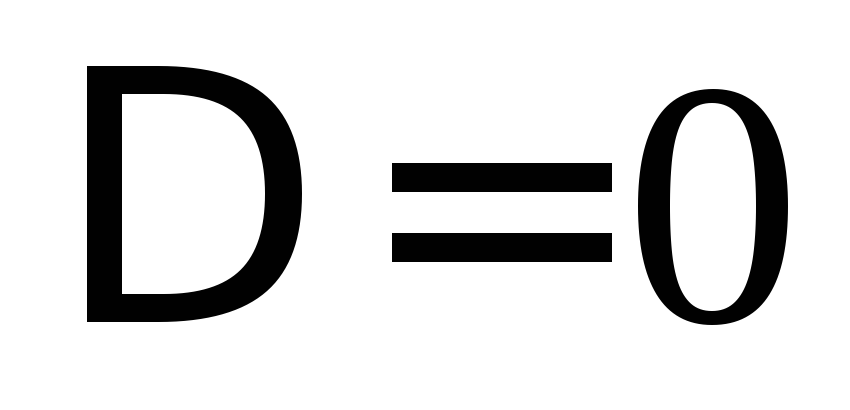 ,
т.е.
,
т.е.
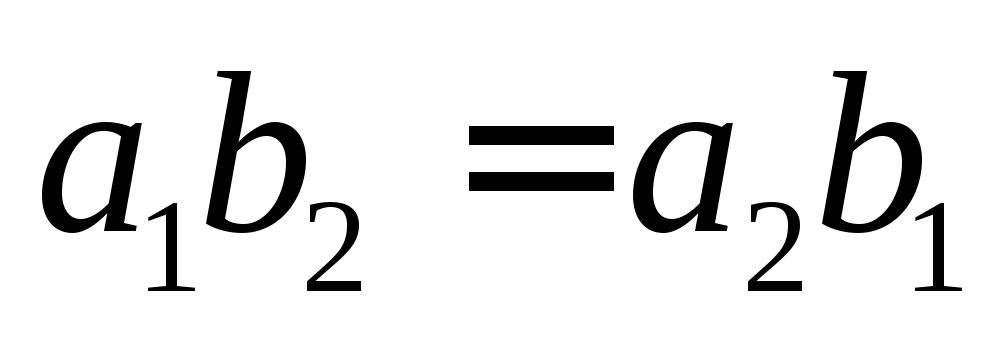 .
Или
.
Или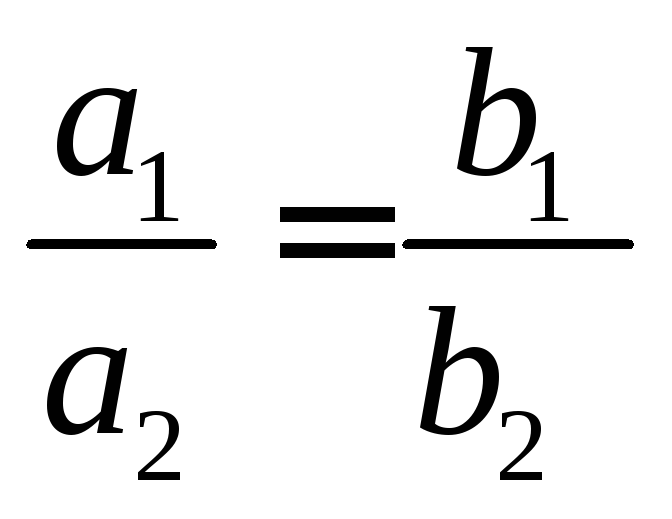
Второе уравнение есть следствие первого.
Например
![]()
§ 3. Система 3-х уравнений с 3-мя неизвестными
Рассмотрим
неоднородную систему
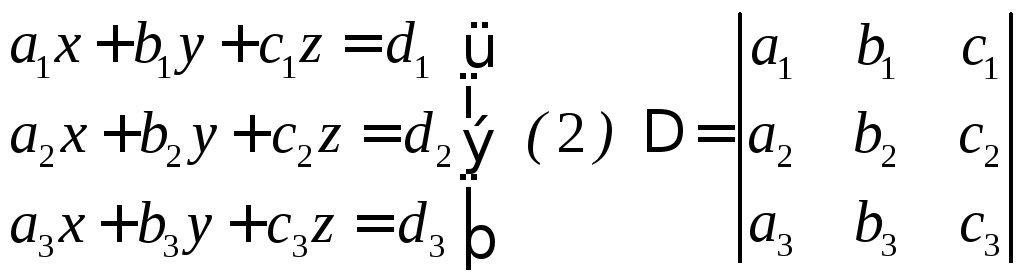
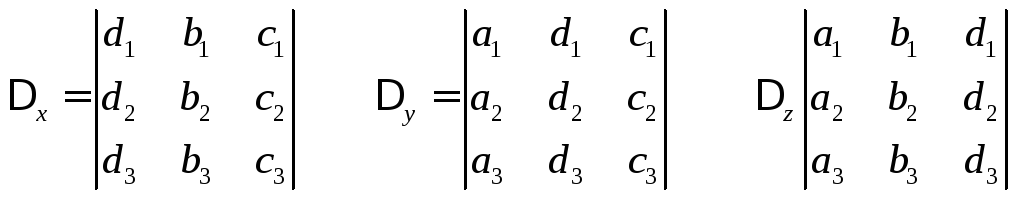
Если
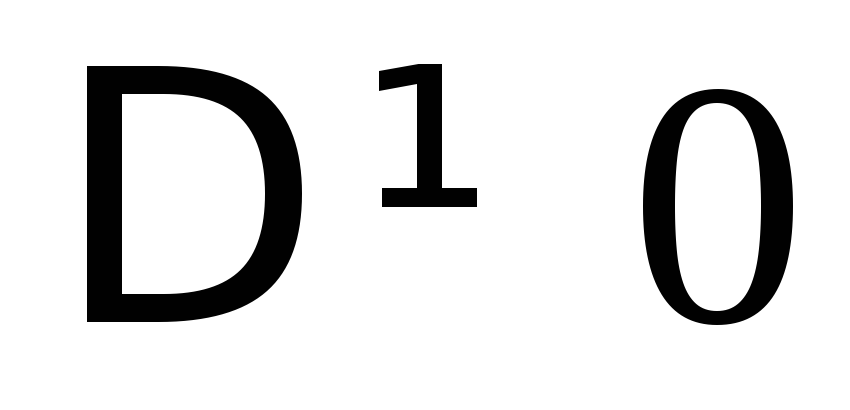 ,
то имеем единственное решение
,
то имеем единственное решение
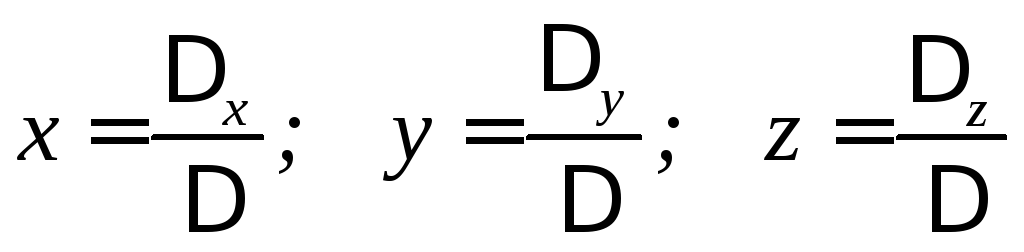
Если
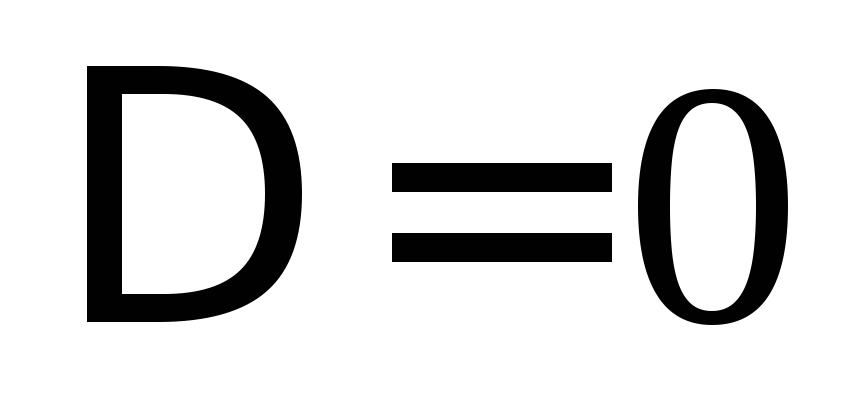 ,
то могут быть такие случаи.
,
то могут быть такие случаи.
Пусть
элементы двух строк определителя
![]() пропорциональны: (например
пропорциональны: (например
![]() )
в этом случае если:
)
в этом случае если:
а)
![]() если и третье уравнение не противоречит
первому, то система имеет множество
решений.
если и третье уравнение не противоречит
первому, то система имеет множество
решений.
Например:
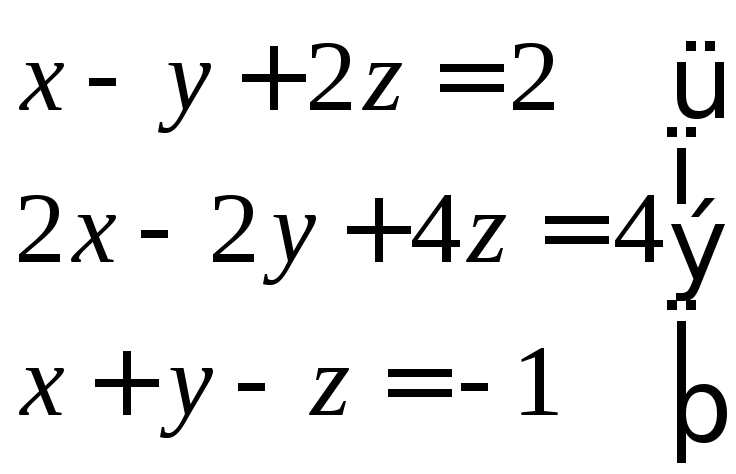 (3)
(3)
Здесь
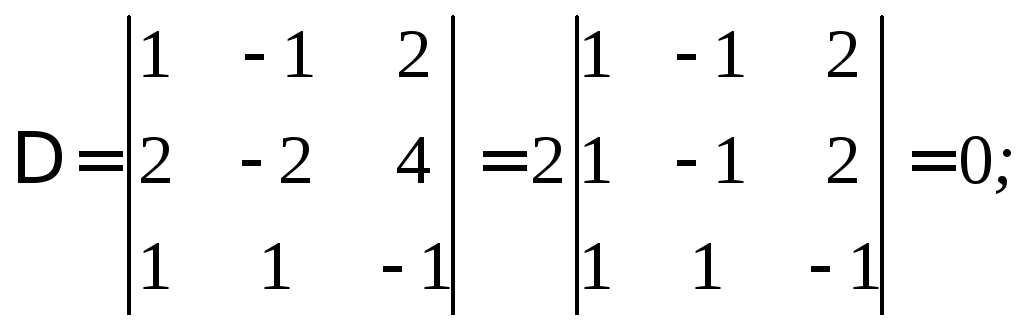
Вместо
первого и второго уравнения системы
(3) будет
![]()
![]()
б)
![]() система несовместна. Например
система несовместна. Например
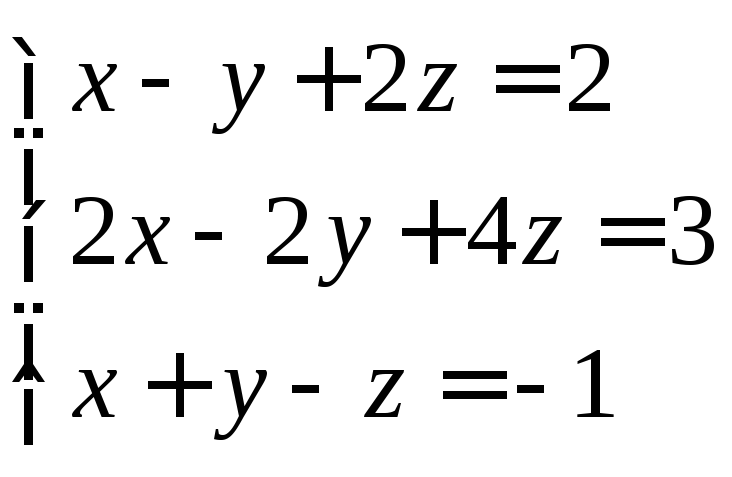
Рассмотрим однородные уравнения
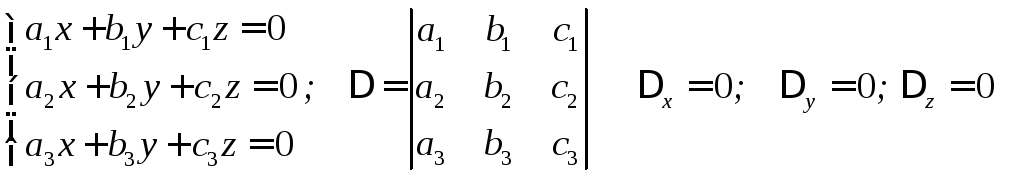
Если
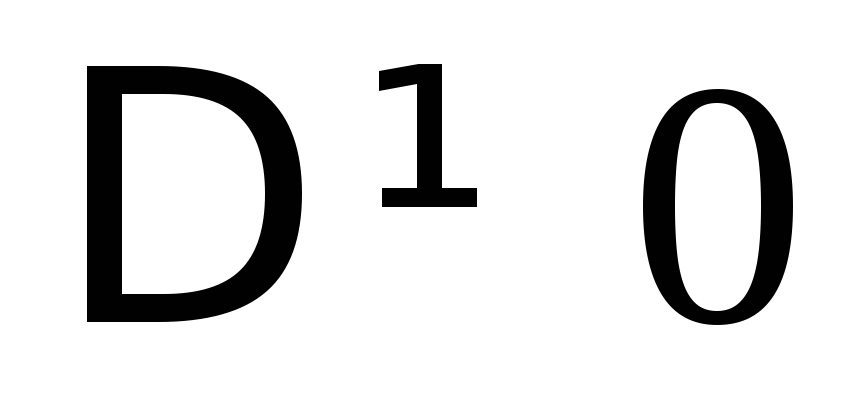 ,
то система имеет единственное решение
,
то система имеет единственное решение
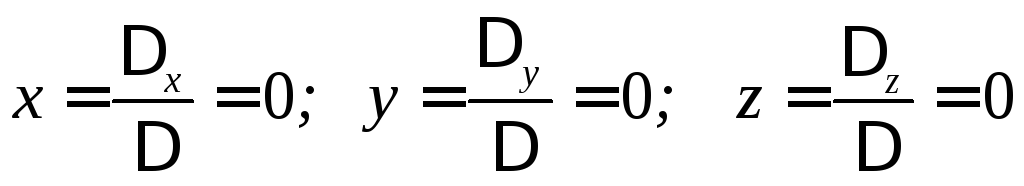 .
.Если
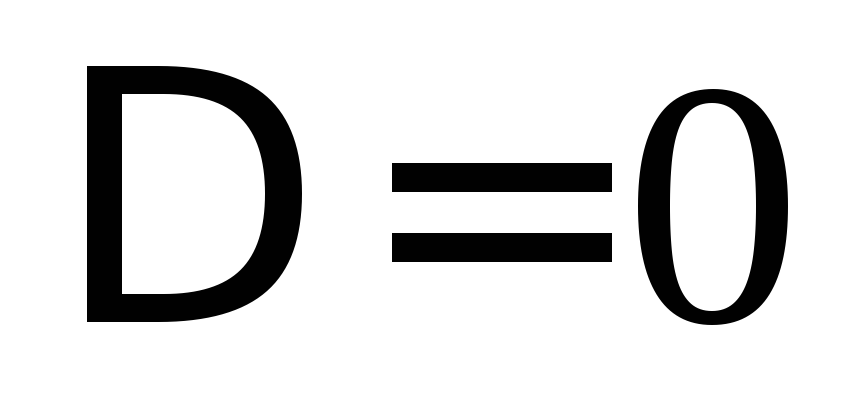 ,
то
,
то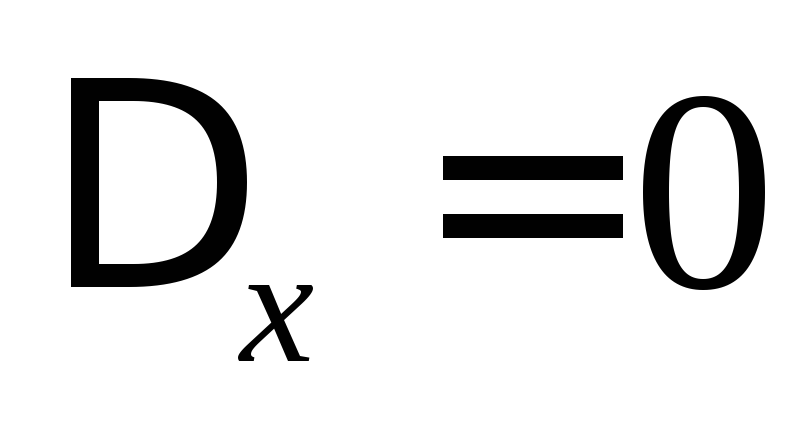 ,
,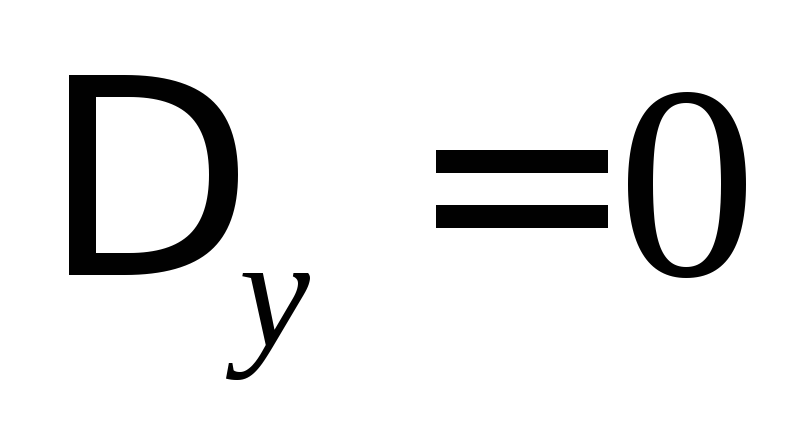 ,
,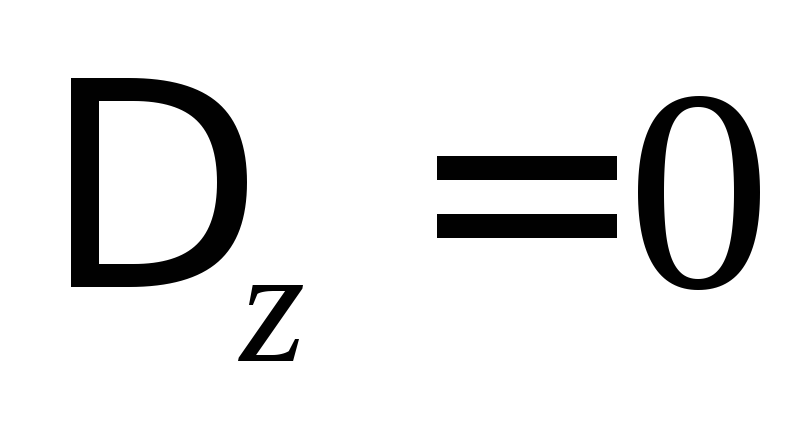 .
.
Система имеет множество решений.
Например:
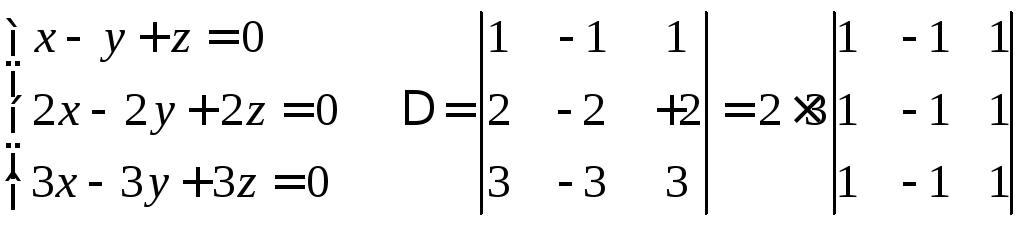
![]() .
Вместо 3-х уравнений получаем одно
.
Вместо 3-х уравнений получаем одно
![]() ,
которое допускает множество решений.
,
которое допускает множество решений.
Вопросы для самоконтроля
Определители 2-го и 3-го порядков, их вычисление и свойства.
Минор, алгебраическое дополнение элемента. Вычисление определителя разложением по элементам ряда. Понятие об определителях произвольного порядка.
Понятие матрицы. Виды матриц. Линейные операции над матрицами. Умножение матриц.
Матрица, обратная данной. Алгоритм её нахождения.
Понятие о системах m линейных алгебраических уравнений с n неизвестными. Общая схема исследования.
Понятие о ранге матрицы. Методы его вычисления. Условие совместности СЛАУ.
Решение системы линейных алгебраических уравнений с помощью формул Крамера.
Решение системы линейных алгебраических уравнений средствами матричного исчисления.
Элементарные преобразования. Метод Гаусса решения СЛАУ.
Основные и свободные неизвестные. Решение СЛАУ для случая m = n.
Исследование однородных систем линейных уравнений.
