- •Высшая математика конспект лекций
- •1 Курс, 1 семестр
- •Содержание
- •Тема 1 «Элементы линейной алгебры» 7
- •Тема 2 «Элементы векторной алгебры» 22
- •Тема 3 «Элементы аналитической геометрии» 30
- •Тема 4 «Введение в анализ» 51
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» 66
- •Введение
- •Тематический план
- •§ 2. Определители 3-го порядка
- •§ 3. Миноры и алгебраические дополнения
- •§ 1. Определители высших порядков.
- •Система двух уравнений с двумя неизвестными
- •Система 3-х уравнений первой степени с 3-мя неизвестными
- •Понятие о матрицах
- •Сложение матриц и умножение их на число
- •Транспонирование матриц
- •Перемножение матриц
- •Решение систем линейных уравнений методом Гаусса
- •Решение систем 3-х уравнений с 3-мя неизвестными с помощью формул Крамера
- •Исследование систем линейных уравнений
- •§ 1. Общие понятия. Систему уравнений вида
- •§ 2. Система 2-х уравнений с 2-мя неизвестными
- •§ 3. Система 3-х уравнений с 3-мя неизвестными
- •Вопросы для самоконтроля
- •Тема 2 «Элементы векторной алгебры» Основные понятия
- •Линейные операции над векторами
- •Линейная зависимость и независимость векторов
- •Определение координат вектора в данном базисе
- •Системы координат и скалярное произведение векторов Декартова система координат
- •Полярная система координат
- •Скалярное произведение векторов.
- •Векторно-скалярное (смешанное) произведение
- •§ 1. Вычисление объема параллелепипеда
- •§3.Направляющие косинусы
- •Вопросы для самоконтроля
- •Тема 3 «Элементы аналитической геометрии»
- •П 4. Переход от полярных координат к декартовым и обратно
- •Простейшие задачи аналитической геометрии на плоскости п 1. Проекция отрезка на оси координат
- •П 2 .Расстояние между двумя точками на координатной плоскости
- •П 3. Деление отрезка в данном отношении
- •Линии и их уравнения п 1. Понятие уравнения линии
- •П 2. Примеры заданий линий при помощи уравнений
- •П 3. Получение линии как геометрического места точек
- •П 4. Параметрические уравнения линий
- •П 5. Алгебраические линии
- •Прямая на плоскости п 1. Угловой коэффициент
- •П 3. Уравнение прямой, проходящей через данную точку м1 (х1; у1)
- •П 8. Уравнение прямой в отрезках
- •П 9. Нормальное уравнение прямой
- •П. 10. Расстояние от точки до прямой
- •П. 11. Уравнение прямой в полярных координатах
- •П. 3 Эллипс и его каноническое уравнение
- •П.4 Эксцентриситет и директрисы эллипса
- •Гипербола и ее каноническое уравнение
- •П 6. Асимптоты гиперболы
- •П 7. Эксцентриситет и директрисы гиперболы
- •П. 8 Парабола и ее уравнение
- •П. 9 Уравнение эллипса, гиперболы и параболы в полярных координатах
- •Преобразование координат п. 1 Преобразование координат при параллельном сдвиге осей
- •П 3. Преобразование декартовых координат при изменении начала и поворота осей
- •П. 4 Преобразование общего уравнения второй степени не содержащего произведения переменных
- •П 5. Преобразование общего уравнения второго порядка
- •Аналитическая геометрия в пространстве Уравнение прямой
- •Понятие об уравнении плоскости.
- •Уравнения поверхностей
- •Вопросы для самоконтроля
- •Тема 4 «Введение в анализ» Переменные и постоянные величины. Понятие функции.
- •Основные характеристики функций.
- •Основные элементарные функции и их графики.
- •Числовая последовательность.
- •Предел функции.
- •Бесконечно малые величины.
- •Бесконечно большие функции.
- •Соотношение между бесконечно малыми и бесконечно большими функциями.
- •Основные теоремы о пределах.
- •Типы неопределенностей и способы их раскрытия.
- •Первый замечательный предел.
- •Эквивалентные бесконечно малые и основные теоремы о них.
- •Непрерывность функций.
- •Основные теоремы о непрерывных функциях.
- •Вопросы для самоконтроля
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» Определение производной.
- •Геометрический смысл производной.
- •Производные основных элементарных функций.
- •Производная сложной и обратной функции.
- •Дифференцирование неявно заданной функции.
- •Дифференцирование функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Производные высших порядков.
- •Производные высших порядков неявно заданной функции.
- •Производные высших порядков от функций заданных параметрически.
- •Дифференциал функции.
- •Правила вычисления дифференциала.
- •Приложения производной.
- •Исследование функций при помощи производной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Вопросы для самоконтроля
- •Литература
Наибольшее и наименьшее значения функции на отрезке.
Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
Функция достигает своего наибольшего
и наименьшего значения либо во внутренней
точке отрезка
.
Функция достигает своего наибольшего
и наименьшего значения либо во внутренней
точке отрезка
![]() ,
либо на границе х0=а
или х0=b.
Если
,
либо на границе х0=а
или х0=b.
Если
![]() ,
то х0
критическая точка данной функции.
,
то х0
критическая точка данной функции.
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:
Найти критические точки функции, т.е. решить уравнение
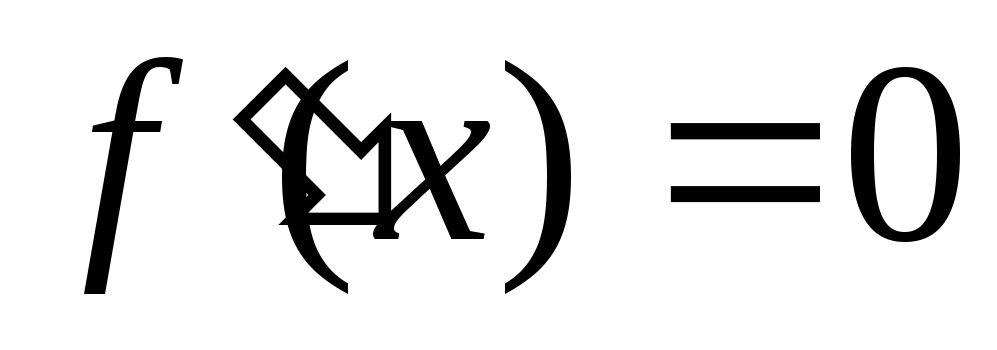 ;
;Вычислить значение функции в тех критических точках, которые принадлежат интервалу
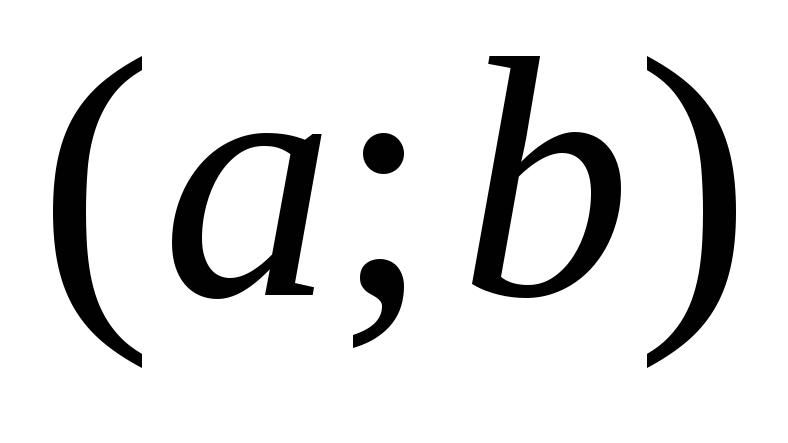 ;
;Вычислить значение функции на концах отрезка, в точках х=а и х=b;
Среди всех полученных значений функции выбрать наибольшее и наименьшее.
Если
функция
![]() на отрезке
на отрезке
![]() не имеет критических точек, то это
означает, что на нем функция монотонна
убывает или возрастает. Следовательно,
наибольшее и наименьшее значение
принимает только на концах отрезка.
не имеет критических точек, то это
означает, что на нем функция монотонна
убывает или возрастает. Следовательно,
наибольшее и наименьшее значение
принимает только на концах отрезка.
Пример:
найти максимум и минимум функции
![]() на отрезке [-2;1].
на отрезке [-2;1].
1.
![]()
х1=0, х2=-1 обе точки принадлежат данному отрезку;
2. f(0)=1 f(-1)=3-4+1=0
3. f(-2)=48-32+1=17 f(1)=3+4+1=8
4. минимальное значение функции на отрезке [-2;1] f(-1)= 0,
максимальное значение функции на отрезке [-2;1] f(-2)=17.
Нахождение наибольшего и наименьшего значения функции широко применяется при решении многих практических задач математики, физики, химии, экономики. Практические задачи: транспортная задача о перевозке груза с минимальными затратами, задача об организации производственного процесса с целью получения максимальной прибыли и т.п. (задачи оптимизации).
Пример: определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение:
Обозначим а- сторона квадратного дна бассейна, h- высота бассейна.
![]() -
площадь поверхности.
-
площадь поверхности.
![]()
![]() -получили
функцию площади. Необходимо найти при
каком значении а
функция будет принимать минимальное
значение.
-получили
функцию площади. Необходимо найти при
каком значении а
функция будет принимать минимальное
значение.
![]() ,
,
![]() ,
,
![]() .
.
Т.к. V=32 м3 , то а=4 м.
![]() вторая
производная больше нуля при а=4м,
следовательно, функция будет достигать
минимального значения при а=4.
Окончательно получили размеры бассейна:
а=4м
и
вторая
производная больше нуля при а=4м,
следовательно, функция будет достигать
минимального значения при а=4.
Окончательно получили размеры бассейна:
а=4м
и
![]() м.
м.
Выпуклость графика функции. Точки перегиба.
График
функции называется выпуклым в интервале
![]() ,
если он расположен ниже касательной,
проведенной в любой точке этого интервала
.
,
если он расположен ниже касательной,
проведенной в любой точке этого интервала
.
Г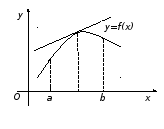
 рафик
функции называется вогнутым в интервале
рафик
функции называется вогнутым в интервале
![]() ,
если он расположен выше касательной,
проведенной в любой точке этого интервала
.
,
если он расположен выше касательной,
проведенной в любой точке этого интервала
.
Точка
графика непрерывной функции
![]() ,
отделяющая его части выпуклости и
вогнутости, называется точкой
перегиба.
,
отделяющая его части выпуклости и
вогнутости, называется точкой
перегиба.
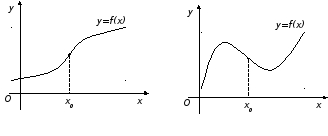
Интервалы выпуклости и вогнутости находятся с помощью следующей теоремы.
Теорема
(достаточное условие выпуклости
(вогнутости)). Пусть функция
![]() имеет вторую производную на интервале
имеет вторую производную на интервале
![]() .
Тогда, если
.
Тогда, если
![]() на этом интервале, то функция выпукла,
если
на этом интервале, то функция выпукла,
если
![]() ,
то график функции вогнутый на этом
интервале.
,
то график функции вогнутый на этом
интервале.
Для
нахождения точек перегиба используются
следующая теорема: (необходимое условие
точки перегиба). Пусть задана функция
![]() .
Если
.
Если
![]() или не существует и при переходе через
точку х0
вторая производная меняет знак, то точка
графика функции с абсциссой
или не существует и при переходе через
точку х0
вторая производная меняет знак, то точка
графика функции с абсциссой
![]() – есть точка перегиба.
– есть точка перегиба.
Точки, в которых вторая производная функции равна нулю или не существует, называются критическими точками 2 –го рода.
Точки перегиба следует искать среди критических точек 2- го рода.
Пример:
исследовать функцию на интервалы
выпуклости, вогнутости, найти точки
перегиба.
![]() .
.
1.
![]()
2.
решаем уравнение
![]() .
Получаем х=0.
.
Получаем х=0.
3.
определяем знак второй производной в
интервалах (-∞; 0) и (0; ∞). На интервале
(-∞; 0) знак второй производной отрицательный
![]() ,
график функции выпуклый. На интервале
(0; ∞)
,
график функции выпуклый. На интервале
(0; ∞)
![]() -
график функции вогнутый.
-
график функции вогнутый.
4.
![]() меняет знак, следовательно, точка (0; 5)
– точка перегиба.
меняет знак, следовательно, точка (0; 5)
– точка перегиба.
Асимптоты графика функции.
Прямая
линия m
называется асимптотой
графика функции
![]() ,
если расстояние d
от точки M,
лежащей на этом графике, до прямой m
стремится к нулю при неограниченном
удалении этой точки по графику от начала
координат в бесконечность.
,
если расстояние d
от точки M,
лежащей на этом графике, до прямой m
стремится к нулю при неограниченном
удалении этой точки по графику от начала
координат в бесконечность.
Асимптоты бывают трех видов: вертикальные, наклонные и горизонтальные.
Прямая
![]() называется вертикальной
асимптотой
графика функции
называется вертикальной
асимптотой
графика функции
![]() ,
если хотя бы один из односторонних
пределов
,
если хотя бы один из односторонних
пределов
![]() и
и
![]() равен бесконечности (
равен бесконечности (![]() ).
).
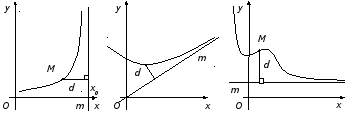
Обычно
вертикальными асимптотами являются
прямые в точках разрыва 2-го рода. Поэтому
для отыскания вертикальных асимптот
определяют точки
![]() бесконечного разрыва функции. Тогда
уравнение вертикальных асимптот
бесконечного разрыва функции. Тогда
уравнение вертикальных асимптот
![]() .
Вертикальные асимптоты могут быть и на
границе области определения функции.
Например, как у функции
.
Вертикальные асимптоты могут быть и на
границе области определения функции.
Например, как у функции
![]() .
.
Пример:
найти асимптоту графика функции
![]() .
.
Точка
х=-1
точка разрыва,
![]() ,
,
![]() .
.
х=-1 – вертикальная асимптота.
Прямая
![]() называется
наклонной
асимптотой
графика функции
называется
наклонной
асимптотой
графика функции
![]() при
при
![]() (при
(при
![]() ),
если
),
если
![]() (соответственно,
(соответственно,
![]() ).
).
Уравнение
наклонной асимптоты к графику функции
![]() ищем
виде
ищем
виде
![]() ,
где
,
где
![]() (*)
(*)
![]() (**)
(**)
Если
хотя бы один из пределов (*) и (**) не
существует или равен бесконечности, то
кривая
![]() наклонной асимптоты не имеет. Асимптоты
графика функции
наклонной асимптоты не имеет. Асимптоты
графика функции
![]() при
при
![]() и
и
![]() могут быть разными. Поэтому при нахождении
пределов (*) и (**) следует отдельно
рассматривать случай, когда
могут быть разными. Поэтому при нахождении
пределов (*) и (**) следует отдельно
рассматривать случай, когда
![]() и когда
и когда
![]() .
.
Частным
случаем наклонной асимптоты (при
![]() )
является горизонтальная
асимптота.
)
является горизонтальная
асимптота.
Прямая
![]() является горизонтальной асимптотой
графика функции
является горизонтальной асимптотой
графика функции
![]() при
при
![]() (при
(при
![]() )
тогда и только тогда, когда
)
тогда и только тогда, когда
![]() (соответственно,
(соответственно,
![]() ).
).
Пример:
для функции
![]()
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() горизонтальная асимптота (ось Ох).
горизонтальная асимптота (ось Ох).
Общая схема исследования функции и построение графиков функций.
При
построении графика данной функции
![]() целесообразно пользоваться следующей
схемой:
целесообразно пользоваться следующей
схемой:
найти область определения функции;
исследовать функцию на четность, нечетность и периодичность;
найти точки пересечения графика с осями координат (если это возможно);
найти интервалы знакопостоянства функции (промежутки, на которых
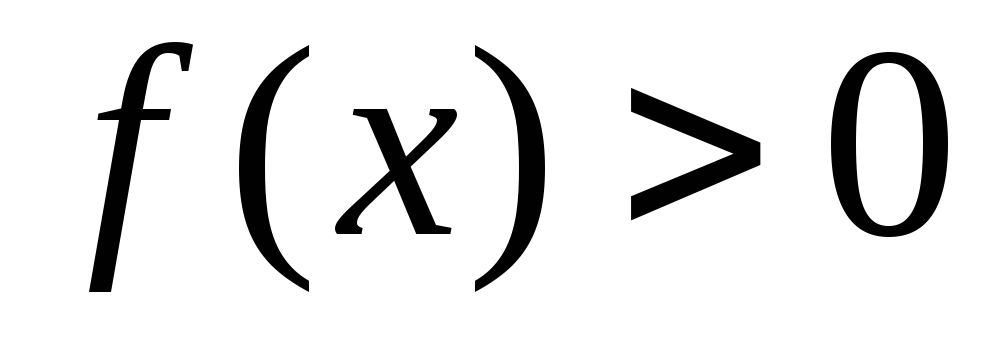 и
и
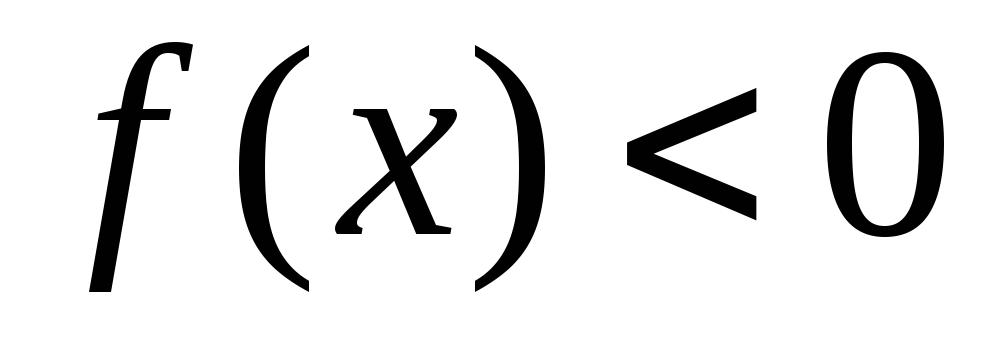 );
);найти асимптоты;
найти интервалы возрастания и убывания, экстремумы функции;
найти интервалы выпуклости и вогнутости, точки перегиба;
построить график функции.
Приведенная схема исследования не является обязательной. В более простых случаях достаточно выполнить лишь несколько операций, например 1, 3, 4, 6. Иногда бывает необходимым вычислить несколько дополнительных точек.
Пример
1.
Исследовать функцию и построить график
![]() .
.
Область определения функции
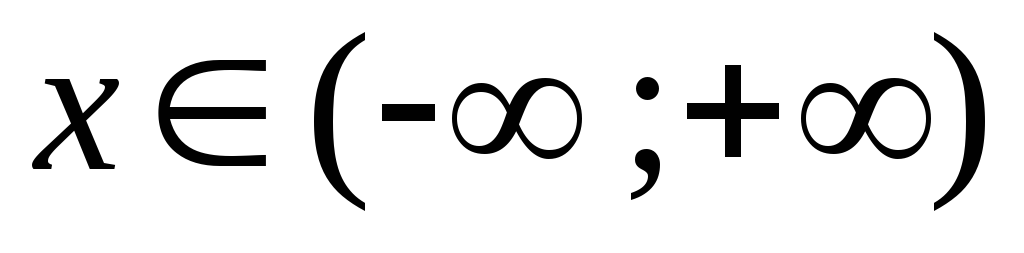 ;
;Исследуем функцию на четность и нечетность:
 .
Получили,
.
Получили,
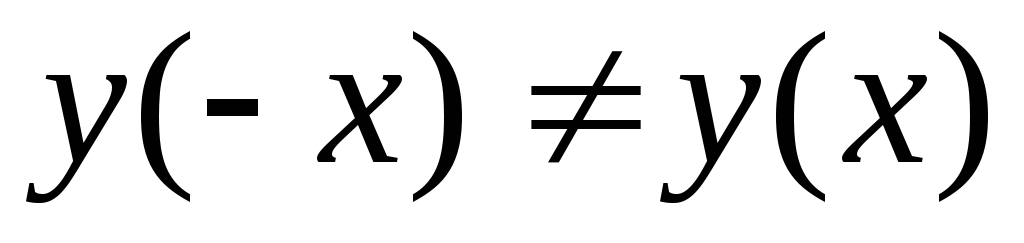 и
и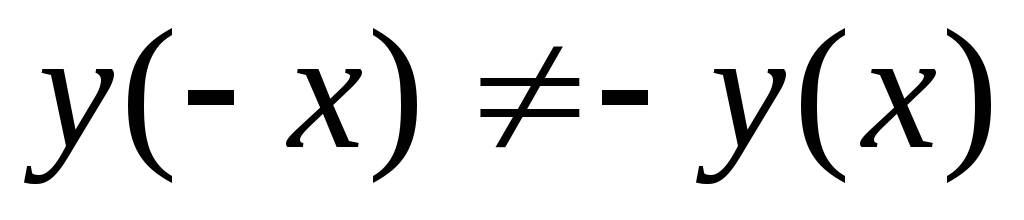 ,
т.е. данная функция общего вида.
,
т.е. данная функция общего вида.Находим точки пересечения с осями координат:
при
![]() ,
,
при
![]() решаем уравнение
решаем уравнение![]()
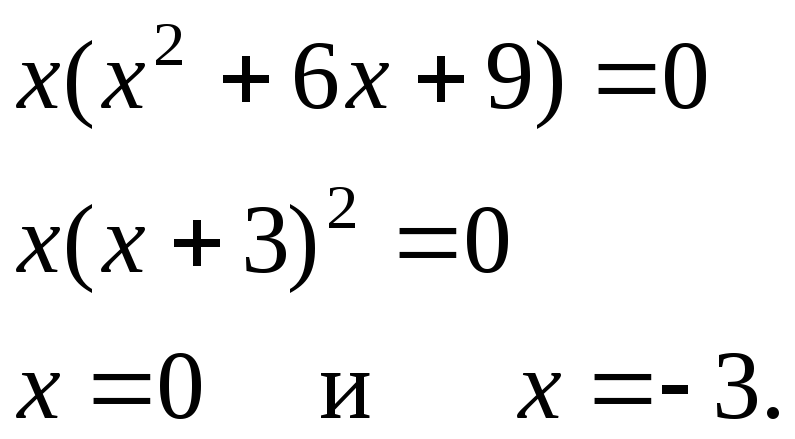
Точки пересечения (0; 0) и (-3; 0).
Найдем интервалы возрастания и убывания функции, экстремумы. Для этого найдем производную
 и решим уравнение
и решим уравнение
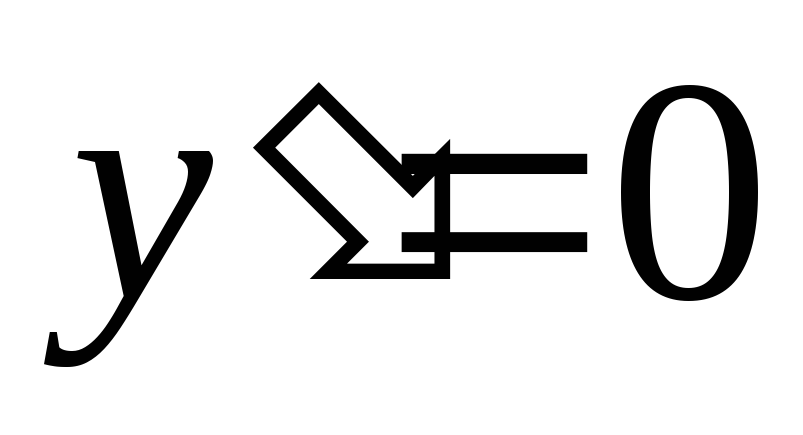 .
.
![]()
Производная
обращается в ноль при
![]() или
или
![]() .
.
Критические
точки
![]()

Для проверки достаточных условий экстремума и определения интервалов убывания, возрастания составим таблицу. Полезно нанести критические точки на числовую ось.
|
|
|
|
|
|
|
|
|
+ |
0 |
|
0 |
+ |
|
|
Возрастает
|
0 max |
У
|
-4 min |
Возрастает
|
Производная
сохраняет знак в каждом из указанных
интервалов. Для его определения выберем
в каждом интервале пробную точку и
определим знак производной в этой точке.
Например, в первом интервале
![]() выберем точку
выберем точку
![]() .
Вычислим
.
Вычислим
![]() ,
производная больше нуля, функция на
этом интервале возрастает и т.д. При
переходе через точку
,
производная больше нуля, функция на
этом интервале возрастает и т.д. При
переходе через точку
![]() производная меняет знак с «плюса» на
«минус», следовательно, точка (-3; 0) точка
максимума; (-1;-4) - точка минимума.
производная меняет знак с «плюса» на
«минус», следовательно, точка (-3; 0) точка
максимума; (-1;-4) - точка минимума.
Найдем точки перегиба графика функции. Для этого определим вторую производную
 и решим
уравнение
и решим
уравнение
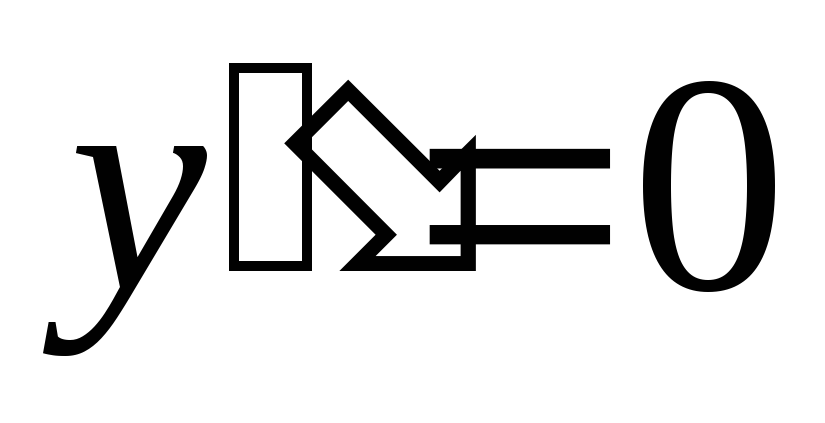 .
.
![]()
![]() -
критическая точка. Для проверки
достаточных условий выпуклости,
вогнутости составим таблицу.
-
критическая точка. Для проверки
достаточных условий выпуклости,
вогнутости составим таблицу.
|
|
|
|
|
|
|
|
0 |
+ |
|
|
Выпуклая
|
-2 Точка перегиба |
Вогнутая
|
На
интервале
![]() вторая производная имеет отрицательный
знак – график функции на этом интервале
выпуклый, на интервале
вторая производная имеет отрицательный
знак – график функции на этом интервале
выпуклый, на интервале
![]() вторая производная положительная –
график функции на этом интервале
вогнутый, точка (-2; -2) - точка перегиба.
вторая производная положительная –
график функции на этом интервале
вогнутый, точка (-2; -2) - точка перегиба.
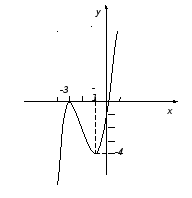
Строим график функции. Находим дополнительные точки
![]()
Пример
2. Исследовать
функцию и построить график
![]() .
.
Область определения
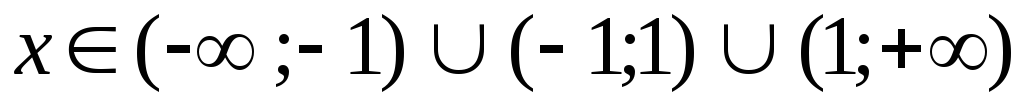 ,
т.е.
,
т.е.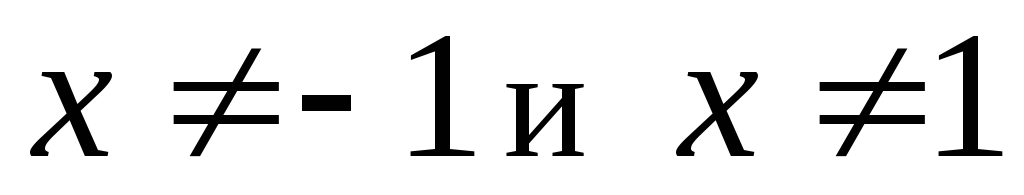 .
.Функция нечетная
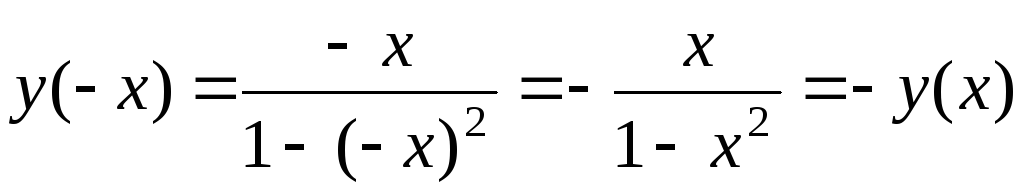 .
.Точка пересечения с осями (0; 0).
Интервалы знакопостоянства. Разложим знаменатель на множители
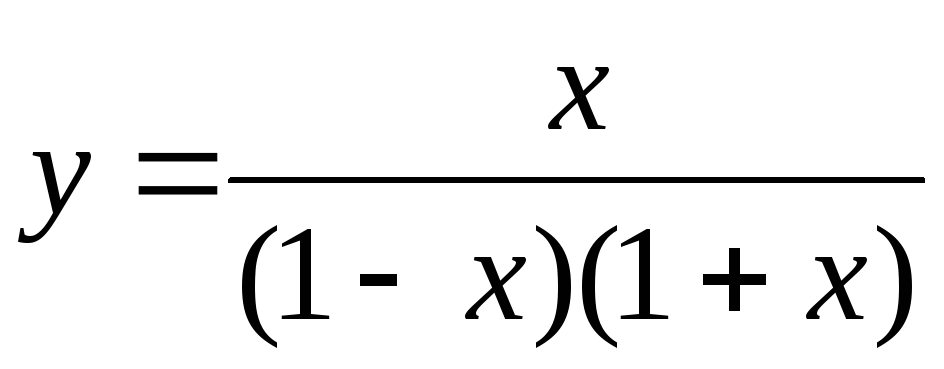 .
На числовой прямой изобразим точки
.
На числовой прямой изобразим точки
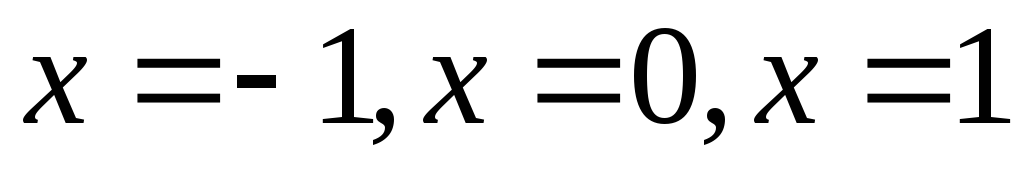 и определим знак функции в каждом из
полученных интервалов.
и определим знак функции в каждом из
полученных интервалов.

На
интервалах
![]() и
и
![]() функция имеет положительный знак, на
интервалах
функция имеет положительный знак, на
интервалах
![]() и
и
![]() - отрицательный.
- отрицательный.
Находим асимптоты. Точки с абсциссами
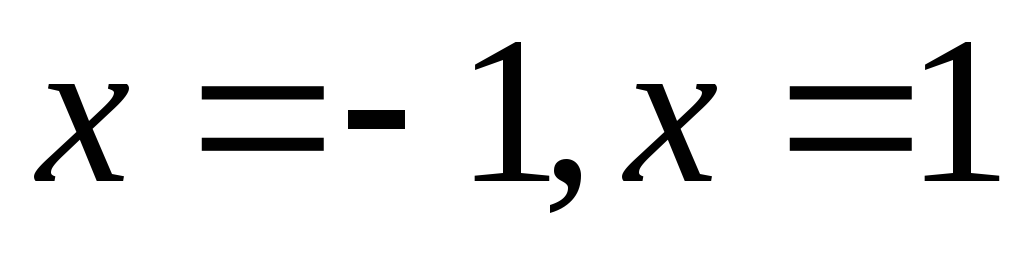 являются точками разрыва, следовательно,
вертикальные асимптоты прямые
являются точками разрыва, следовательно,
вертикальные асимптоты прямые
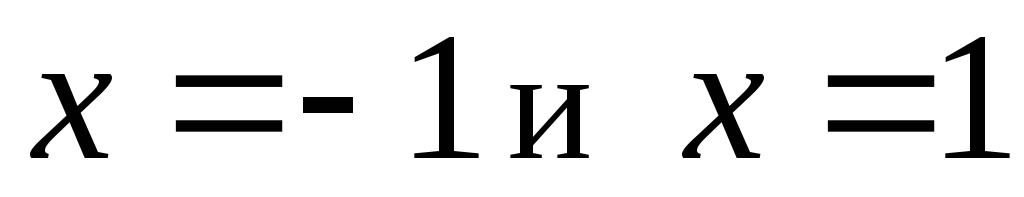 .
Определим
односторонние пределы в этих точках.
.
Определим
односторонние пределы в этих точках.
![]()
![]()
![]()
![]()
Наклонную
асимптоту будем искать в виде
![]() .
.
![]()
![]()
Получили:
![]() - горизонтальная асимптота.
- горизонтальная асимптота.
Находим интервалы убывания, возрастания, экстремумы функции. Для этого найдем производную
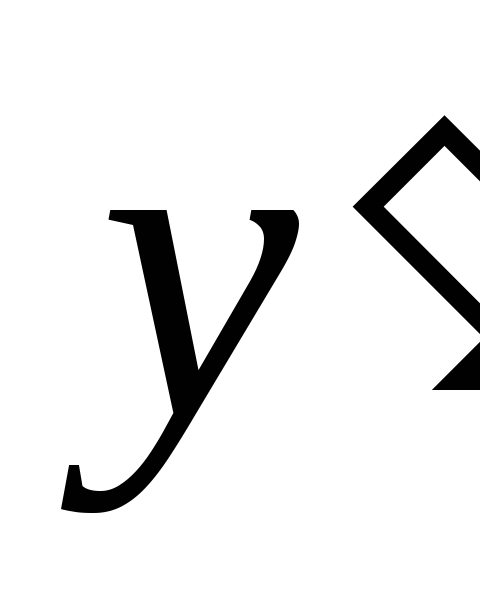 и решим уравнение
и решим уравнение
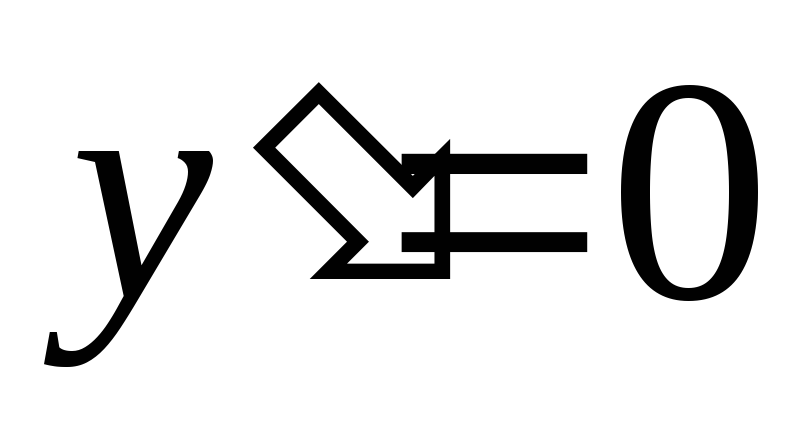 .
.
![]()
![]()
Производная
не обращается в нуль ни в одной точке.
В точках
![]() производная не существует, но эти точки
не принадлежат области определения,
поэтому точек экстремума нет. На числовой
прямой изображаем точки
производная не существует, но эти точки
не принадлежат области определения,
поэтому точек экстремума нет. На числовой
прямой изображаем точки
![]() и определяем интервалы убывания и
возрастания функции.
и определяем интервалы убывания и
возрастания функции.
В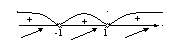 каждом из интервалов производная имеет
положительный знак,
каждом из интервалов производная имеет
положительный знак,
следовательно функция возрастает на всей области определения.
Определяем точки перегиба, интервалы выпуклости и вогнутости. Находим вторую производную и решаем уравнение
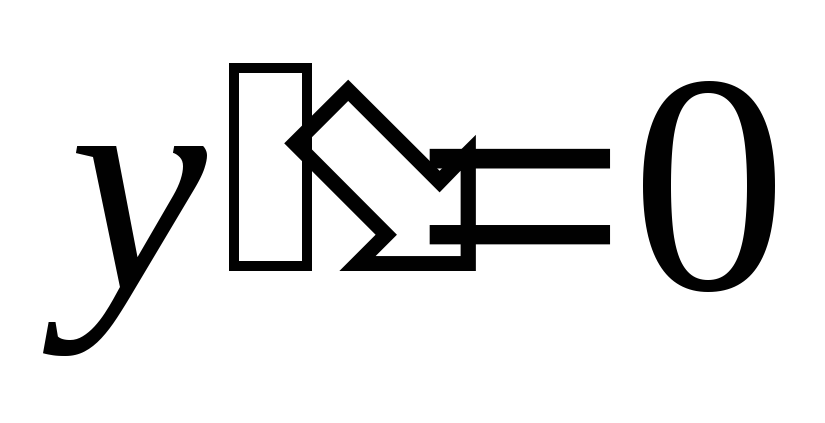 .
.
![]()
Критические
точки
![]() .
Для проверки достаточных условий
выпуклости, вогнутости составляем
таблицу.
.
Для проверки достаточных условий
выпуклости, вогнутости составляем
таблицу.
|
|
|
|
|
|
|
|
|
+ |
|
0 |
+ |
─ |
|
|
Вогнутая |
Выпуклая |
0 Точка перегиба |
Вогнутая |
Выпуклая |
8)
Строим график функции. Дополнительные
точки
![]()
П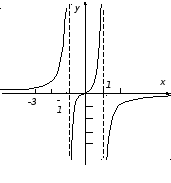 ример
3.
ример
3.![]()
область определения
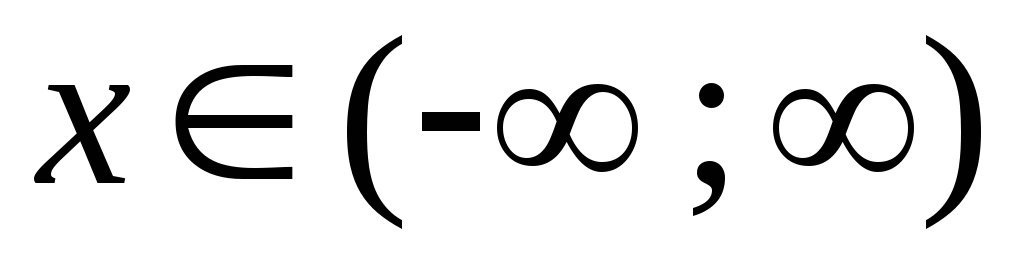 ;
;точка пресечения с осями координат (0; 0);
функция не является четной или нечетной, функция общего вида;
если х<0, то у<0; если х>0, то у>0 – интервалы знакопостоянства;
находим асимптоты:
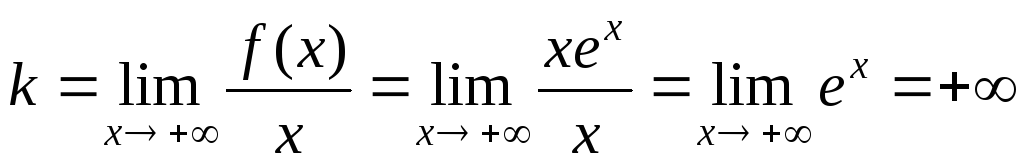 ,
график функции при
,
график функции при
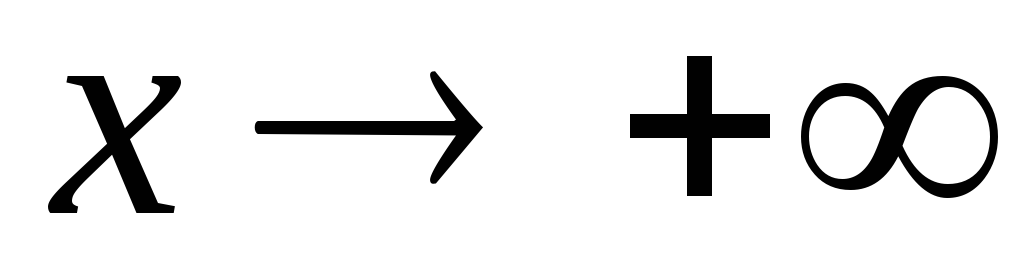 асимптоты
не имеет;
асимптоты
не имеет;
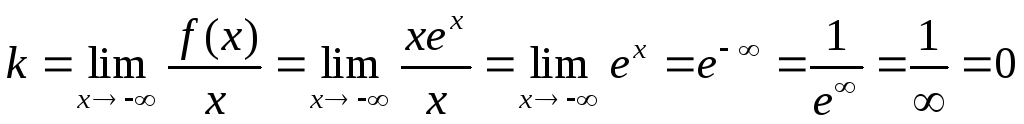 ,
,
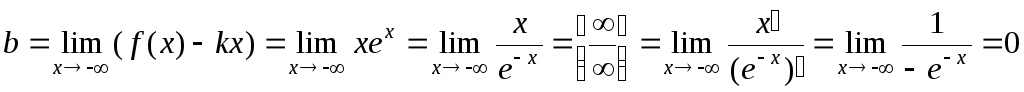 при
при
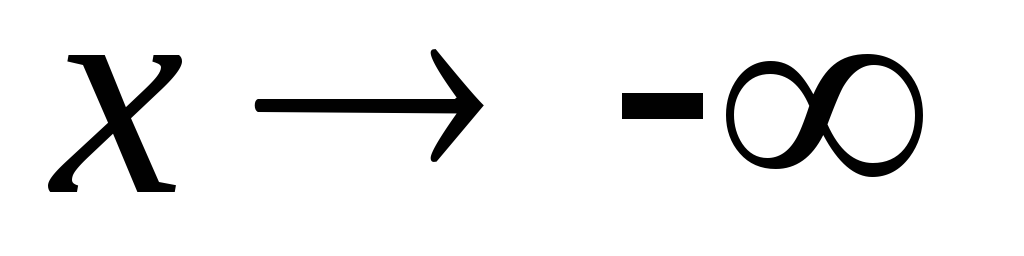 график функции имеет горизонтальную
асимптоту у=0;
график функции имеет горизонтальную
асимптоту у=0;находим точки экстремума, интервалы возрастания, убывания.
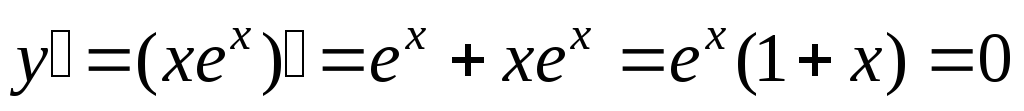 при х=-1.
На интервале (-∞; -1) производная
отрицательная
при х=-1.
На интервале (-∞; -1) производная
отрицательная
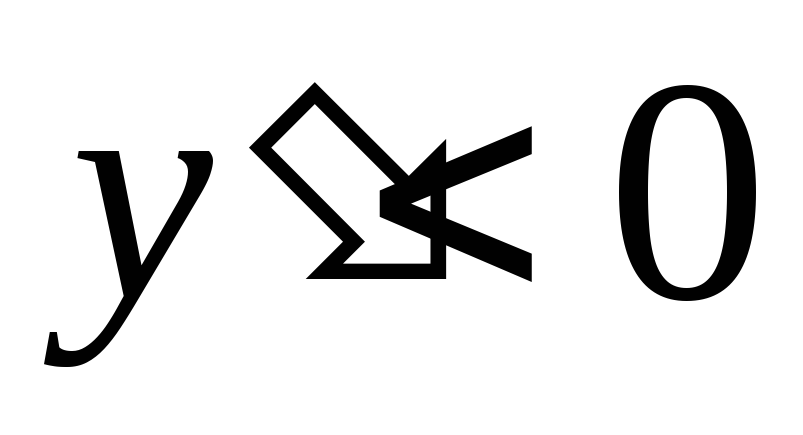 ,
следовательно на этом интервале функция
убывает, на интервале (-1;∞) производная
положительная
,
следовательно на этом интервале функция
убывает, на интервале (-1;∞) производная
положительная
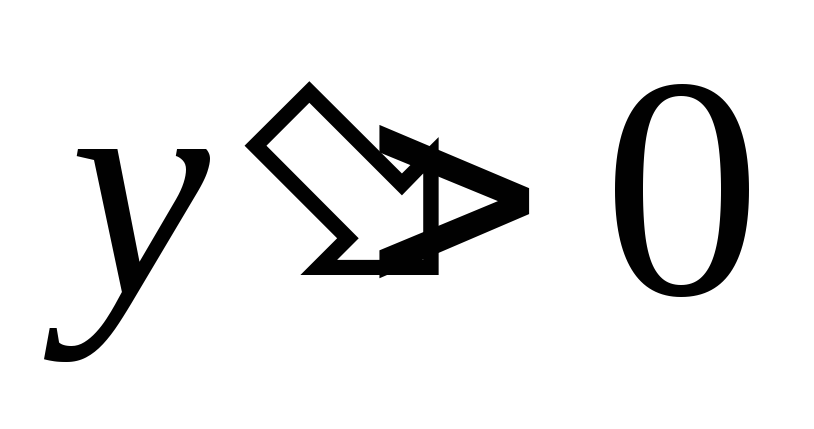 , функция здесь возрастает. Точка
х=-1
точка минимума,
, функция здесь возрастает. Точка
х=-1
точка минимума,
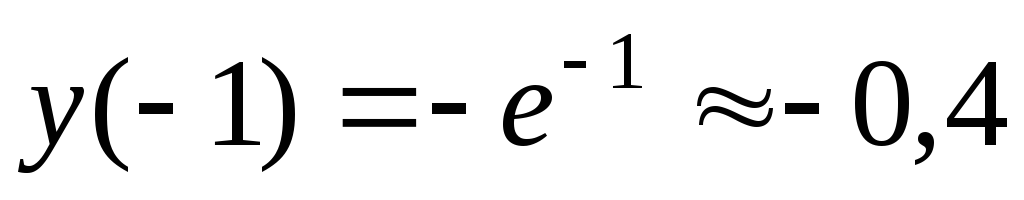 .
.находим интервалы выпуклости, вогнутости, точки перегиба.
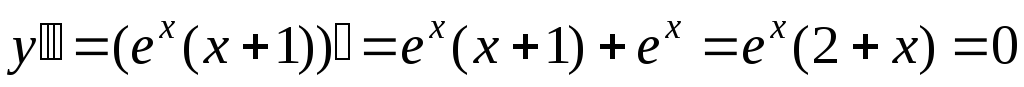 при х=-2.
На интервале (-∞;-2) знак второй
производной отрицательный
при х=-2.
На интервале (-∞;-2) знак второй
производной отрицательный
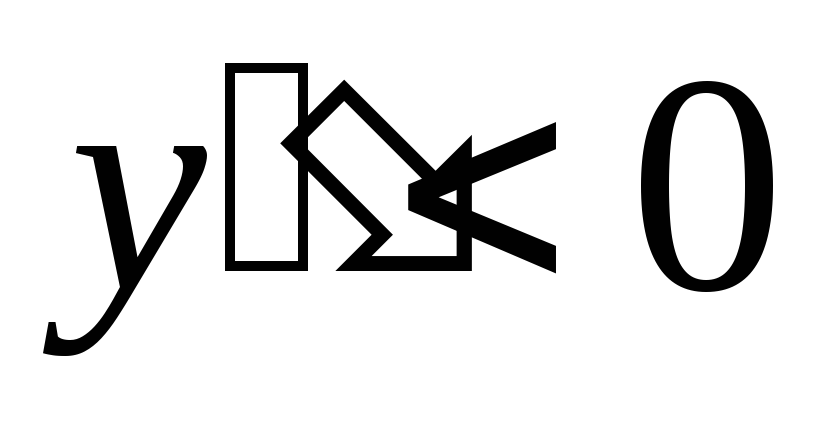 -график функции выпуклый; на интервале
(-2;∞) знак второй производной положительный
-график функции выпуклый; на интервале
(-2;∞) знак второй производной положительный
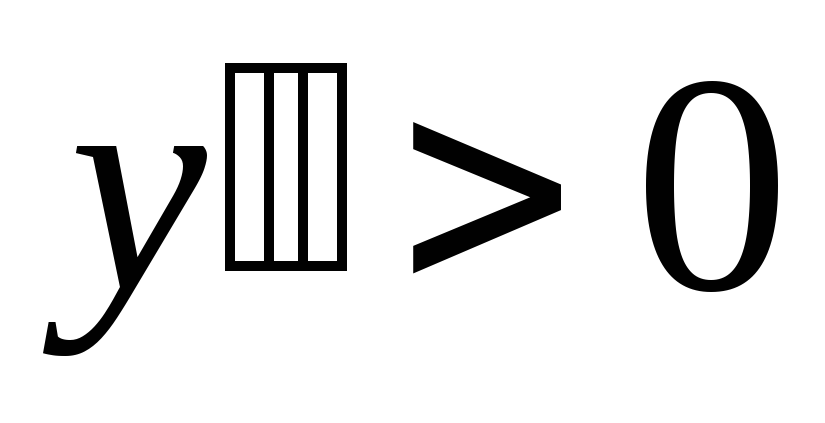 -
график функции вогнутый. Точка
х=-2
точка перегиба,
-
график функции вогнутый. Точка
х=-2
точка перегиба,
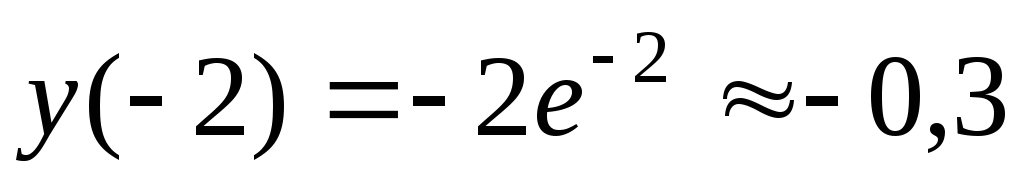 .
.с
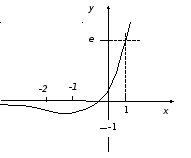 троим
график функции. Дополнительные точки
троим
график функции. Дополнительные точки
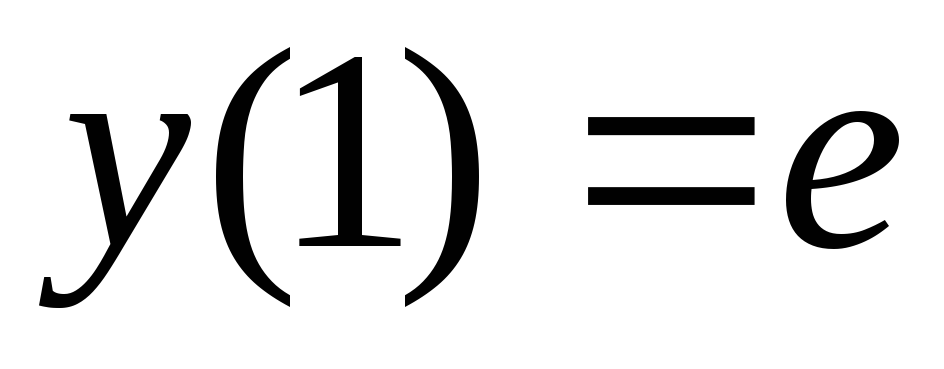 .
.


 бывает
бывает