Производные основных элементарных функций.

1. Производная степени.

Производная степенной функции равна показателю степени, умноженному на степень с показателем на единицу ниже данного.

2. Производные тригонометрических функций.

Воспользуемся определением производной.

Так как, , то

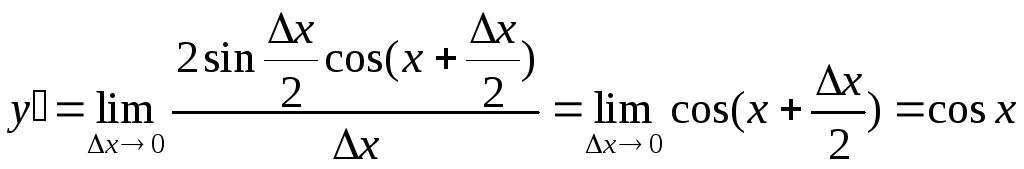
Таким образом, .

Аналогично можно показать, что .

. Так как, , то согласно правилу дифференцирования дроби получаем

Таким образом, .

Доказать самостоятельно, что .

Производная сложной и обратной функции.

Пусть и , тогда сложная функция с промежуточным аргументом и независимым аргументом .

Теорема. Если функция имеет производную в точке х, а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке х, которая находится по формуле

.

Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.

Пример. Найти производную сложной функции .

Теорема. Если функция строго монотонна на интервале (а; в) и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция так же имеет производную , определяемую равенством или .

Пример. Найти производную функции .

Обратная функция для исходной . .

.

3. Производная показательной функции 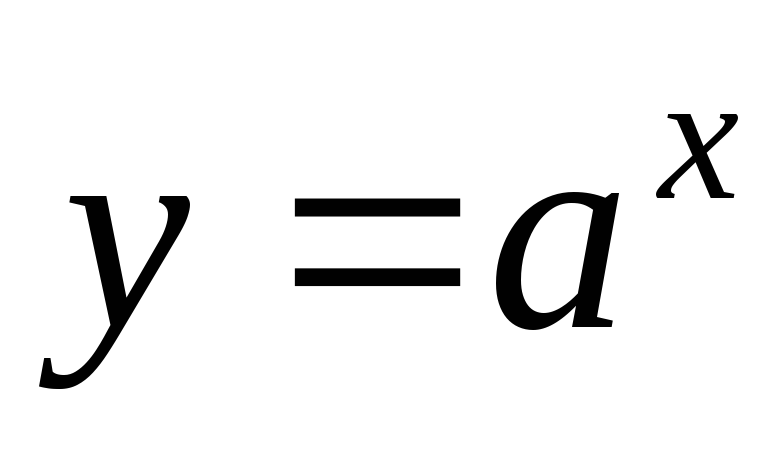, где .

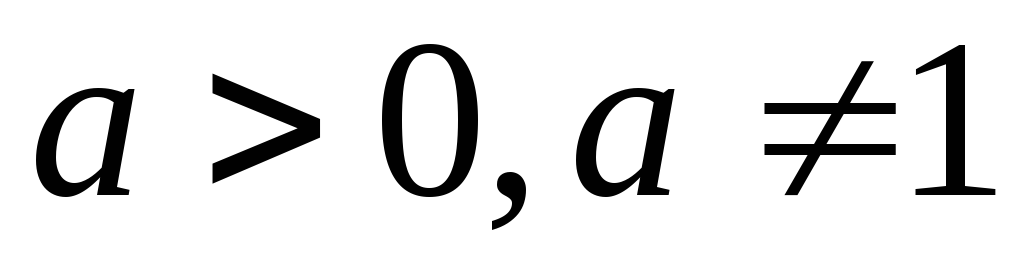Найдем сначала производную функции , придав аргументу х приращение ∆х находим приращение функции ∆у.

, по определению производной

Использовали эквивалентность б.м. функций при .

Получили .

Теперь рассмотрим функцию , её можно записать .

По формуле производной сложной функции находим

.

Таким образом, производная показательной функции .

4. Производная логарифмической функции 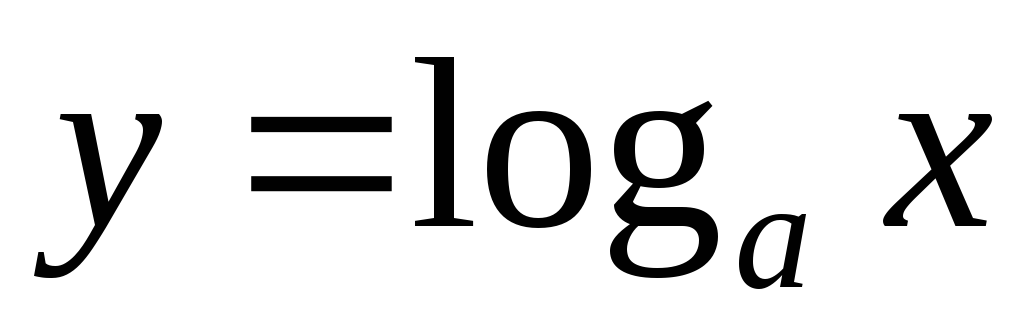, где .

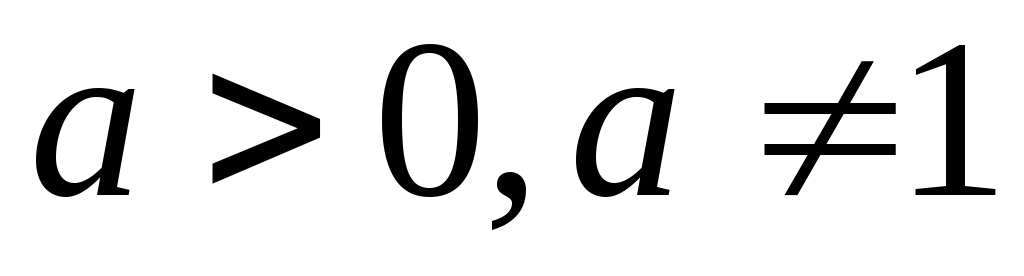Рассмотрим функцию . Найдем производную этой функции, пользуясь определением производной

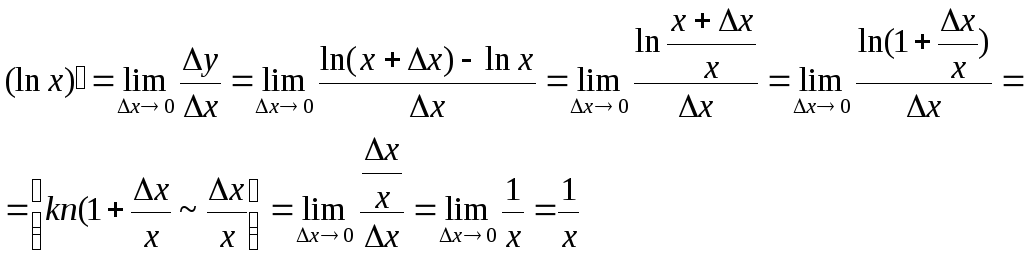
Таким образом .

Вернемся к функции . Т.к. , находим

.

Получили .

5. Производные обратных тригонометрических функций.

, обратная ей . По правилу дифференцирования обратной функции находим

, перед корнем взят знак «+» так как при . Таким образом .

Функции и связаны соотношением

, отсюда находим . Далее

.

Для функций и действуем аналогично.

обратная ей .

.

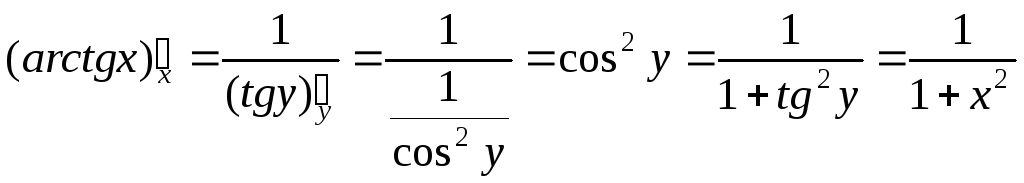Т.к , находим .

.

6. Гиперболические функции и их производные.

- гиперболический синус.

- гиперболический косинус.

гиперболический тангенс, - гиперболический котангенс.

Производные

Таблица производных.

Правила дифференцирования:

1.

2. с-const

3. с-const

4. , если , т.е.

5. , если и - обратные функции.

Формулы дифференцирования.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Примеры:

1.

2.

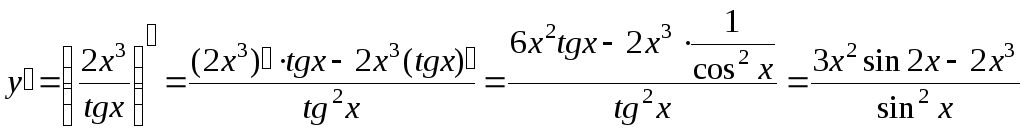
3.