T = ˜ fv1

The default values for the modeling parameters are:

Pseudo Time Stepping for Turbulent Flow Models is the default applied to the stationary form of the Spalart-Allmaras model.

W A L L B O U N D A R Y C O N D I T I O N S

The Spalart-Allmaras model is consistent with a no-slip boundary condition, that is

u 0. Since, there can be no fluctuations on the wall, the boundary condition for is

0.

The Spalart-Allmaras model can be considered to be well resolved at a wall if lc* in order of unity. lc* is the distance, measured in viscous units, from the wall to the center of the wall adjacent cell and can be evaluated as the boundary variable

Dimensionless distance to cell center. See also Wall for boundary condition details.

I N I T I A L V A L U E S

The default initial values for the Spalart-Allmaras interface are

u = 0 p = 0

˜

= --

Inlet Values for the Turbulence Length Scale and Intensity

A value of 0.1% is a low turbulence intensity IT. Good wind tunnels can produce values of as low as 0.05%. Fully turbulent flows usually have intensities between five and ten percent.

The turbulent length scale LT is a measure of the size of the eddies that are not resolved. For free-stream flows these are typically very small (in the order of

T H E O R Y F O R T H E TU R B U L E N T F L O W I N T E R F A C E S | 157

centimeters). The length scale cannot be zero, however, because that would imply infinite dissipation. Use the following table as a guideline when specifying LT (Ref. 3):

TABLE 4-9: TURBULENT LENGTH SCALES FOR TWO-DIMENSIONAL FLOWS

Pseudo Time Stepping for Turbulent Flow Models

Pseudo time stepping is per default applied to the turbulence equations for stationary

problems, both for 2D models as well as 3D models. The turbulence equations use the

same ˜ as the momentum and continuity equations. t

If the automatic expression for CFLloc is

1.3min niterCMP-1 9 +

if niterCMP 25 9 1.3min niterCMP – 25 9 0 + if niterCMP 50 90 1.3min niterCMP – 50 9 0

for 2D and

1.3min niterCMP-1 9 +

if niterCMP 30 9 1.3min niterCMP – 30 9 0 + if niterCMP 60 90 1.3min niterCMP – 60 9 0

for 3D.

158 | C H A P T E R 4 : S I N G L E - P H A S E F L O W B R A N C H

References for the Single-Phase Flow, Turbulent Flow Interfaces

1.D.C. Wilcox, Turbulence Modeling for CFD, 2nd ed., DCW Industries, 1998.

2.D.M. Driver and H.L. Seegmiller, “Features of a Reattaching Turbulent Shear Layer in Diverging Channel Flow,” AIAA Journal, vol. 23, pp. 163–171, 1985.

3.H.K. Versteeg and W. Malalasekera, An Introduction to Computational Fluid Dynamics, Prentice Hall, 1995.

4.A. Durbin, “On the k- Stagnation Point Anomality,” International Journal of Heat and Fluid Flow, vol. 17, pp. 89–90, 1986.

5.A, Svenningsson, Turbulence Transport Modeling in Gas Turbine Related Applications,” doctoral dissertation, Department of Applied Mechanics, Chalmers University of Technology, 2006.

6.C. H. Park and S.O. Park, “On the Limiters of Two-equation Turbulence Models,”

International Journal of Computational Fluid Dynamics, vol. 19, No. 1, pp. 79– 86, 2005.

7.J. Larsson, Numerical Simulation of Turbulent Flows for Turbine Blade Heat Transfer, doctoral dissertation, Chalmers University of Technology, Sweden, 1998.

8.L. Ignat, D. Pelletier, and F. Ilinca, “A Universal Formulation of Two-equation Models for Adaptive Computation of Turbulent Flows,” Computer Methods in Applied Mechanics and Engineering, vol. 189, pp. 1119–1139, 2000.

9.D. Kuzmin, O. Mierka, and S. Turek, “On the Implementation of the k-

Turbulence Model in Incompressible Flow Solvers Based on a Finite Element Discretization,” International Journal of Computing Science and Mathematics, vol. 1, no. 2–4, pp. 193–206, 2007.

10.H. Grotjans and F.R. Menter, “Wall Functions for General Application CFD Codes,” ECCOMAS 98, Proceedings of the Fourth European Computational Fluid Dynamics Conference, John Wiley & Sons, pp. 1112–1117, 1998.

11.K. Abe, T. Kondoh, and Y. Nagano, “A New Turbulence Model for Predicting Fluid Flow and Heat Transfer in Separating and Reattaching Flows—I. Flow field calculations,” International Journal of Heat and Mass Transfer, vol. 37, no. 1, pp. 139–151, 1994.

12.The Spalart-Allmaras Turbulence Model, http://turbmodels.larc.nasa.gov/spalart.html.

T H E O R Y F O R T H E TU R B U L E N T F L O W I N T E R F A C E S | 159

T h e o r y f o r t h e R o t a t i n g M a c h i n e r y I n t e r f a c e s

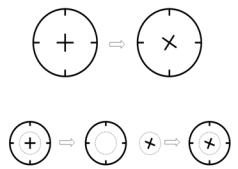
The Single-Phase Flow, Rotating Machinery Interfaces models moving rotating parts in, for example, stirred tanks, mixers, and pumps. The interfaces formulate the Navier-Stokes equations in a rotating coordinate system. Parts that are not rotated are expressed in the fixed material coordinate system. The rotating and fixed parts need to be coupled together by an identity pair, where a flux continuity boundary condition is applied.

Use these interfaces where it is possible to divide the modeled device into rotationally invariant geometries. The operation can be, for example, to rotate an impeller in a baffled tank, as in Figure 4-7 where the impeller rotates from position 1 to 2. The first step is to divide the geometry into two parts that are both rotationally invariant, as shown in Step 1a. The second step is to specify the parts to model using a rotating frame and the ones to model using a fixed frame (Step 1b). The predefined coupling then automatically does the coordinate transformation and the joining of the fixed and moving parts (Step 2a).

Figure 4-7: The modeling procedure in the Rotating Machinery, Fluid Flow interface.

It is straightforward to use the coupling. First draw the geometry using two separate domains for the fixed and rotating parts. Then activate the assembly (using an assembly instead of a union) and create an identity pair, which makes it possible to treat the two domains as separate parts in an assembly. After this, specify which part uses a rotating frame. Once this is done, proceed to the usual steps of setting the fluid properties, boundary conditions, and then mesh and solve the problem.

160 | C H A P T E R 4 : S I N G L E - P H A S E F L O W B R A N C H

5

T h i n - F i l m F l o w B r a n c h

The fluid flow interfaces are grouped by type under the Fluid Flow main branch. The interfaces described in this section are found under the Thin-Film Flow branch () in the Model Wizard. The Mechanisms for Modeling Thin-Film Flow Interfaces helps you choose the best one to start with.

In this chapter

•The Lubrication Shell Interface

•The Thin-Film Flow Interface

•Theory for the Thin-Film Flow Interfaces

161