МАТЕМАТИКА 2Ч

5.

7.

9.

11.

13.

15.

17.

19.

21

23.

25.

27.

29.

2y ln y = x2

y2 - 2xy - x2 = 0 y = x + arctg y

x y = y x

(x + y)2 = 9(x - y)

y × sin x = cos(x - y)

y2 = 2x + ln yx

(x + y)3 = 27(x - y)

exy = x + y tg y = x2 y

cos y = xy2 + 3 ctg y = x2 + y x3 + 2xy = 3y2

6.x + y = xy2 - x2 y

8.y2 = 2 + xe y

10.y = cos(x + y)

12.y = sin(x - y)

14.y = 3 + xe y

16.x + y = e y

18.yex = e y+1

20.xy − 0.5sin 2y = x

22.xy = arctg y

24.y = (sin y)x

26.y = e y sin x

28.x + sin y = cos y

7.ìx = 2(t - sin t) íîy = 4(3 + cos t)

9.ìx = ln t

ï

íïy = t -1 î t

13.ìx = t - sin t íîy = 2 - cos t

17.ìx = cos t

íîy = sec t

19.ìx = sin t - t cos t íîy = cos t + t sin t

21.ìïx = t3

í

ïy = ln t

î

52

12.ìx = ln t

íîy = arctg t

18.ìx = sin t

íîy = cos ec(t)

22.ìx = 2(t - sin t) íîy = 2(1 - cos t)

24.ìïx = ln(1 + t 2 )

í

ïy = t - arctg t

î

26.ìx = ln(cos t) íîy = ln(cos 2t)

5.y = x2 ln x

7.y = arctg(x2 )

13.y = e−x cos 3x

15.y = xesin x

17.y = arctgx

19.y = x × arctg x

25.y = e4x+3 × (x3 + 2)

29. = arcsin x y

1 - x2

2.y = (1 + x2 )arctg x

4.y = (2x3 +1)cos 3x

6.y = ln ctg4x

8.y = 3(1 - x)2

10.y = ln ln x

12.y = x3e5x

18.y = ln(x + x )

20.y = x - arctg x

22.y = (3x - 7)× 3−x

24.y = e2x sin 4x

26.y = xe1+x - e1+x

lim (3x2 + 4x) e−3x

1. x→∞

3.lim e2x - 2x -1 x→0 x × sin 3x

7.lim 1 - cos 2x + tg 2 x →0 x sin 3xx

7.y = ln x2 + 4

8.y = - 1x

9.y = 12 ln 2 x + ln x + 2

(y¢)2 +1 = 2 × y × y¢¢

y¢¢ - 2y¢ + y = ex y′′ + 3y′ + 2y = 0

y′′ + 4y = 4x y3 y¢¢ +1 = 0

2(y¢)2 = (y -1) y¢¢

y¢¢(x2 + 4)+ 2xy¢ =1 y y¢¢ = y¢(y2 + y¢)

x2 y¢¢ + x y¢ =1

y¢¢ × y3 =1

y¢¢ + sin 3 x = 2sin x × cos2 x

12.y = (x -1)ex+1 + 2

13.y = (2x2 - 3x)ex - 2e−x + e−3x

14.y =1 - 2e−3x + x3 + 3x2 - 2x

15.y = 2 cos 3x − 5sin 3x + 4x sin 3x

16.y = e−7x × 2x3

17.y = 3e−2x + 2e x 2 - 5sin 2x - 3cos 2x

18.y = -3e2x + 2e−2x - x(2x2 + 3)

19.y = 5 - 2e−3x + 32 x2 - x

20.y = -3cos x + 5sin x + x + ex

22.y = 5x − 3 − ln cos x

23.y = 2ch x 2+1

24.y = e x + e−x

25.y = cos ex + sin ex

26.y = 2e3x - 3e4x - xe4x

27.y = (0,1x2 - 0,04x + 2)e2x - 4e−3x

28.y = ex (3sin x - 2(x +1)cos x)

29.y = sin x × (3 + 0,5x)- 5cos x

30.y = cos 2x + 13 (sin x + sin 2x)

xy¢¢ = y¢ × ln yx′

y¢¢ + 4y¢ + 3y = (16x2 -14)ex

y¢¢ - 9x2 = 24x - 3y¢ y′′ = 24 cos 3x - 9y

y¢¢ + 49y =12xe−7x -14y¢

2y′′ + 3y′ = 2y + 68sin 2x

y¢¢ - 8x3 = 4y y′′ + 3y′ = 9x

y¢¢ - x = 2ex - y

(1 + x2 )y¢¢ = x3 - 2xy¢

y¢¢ × cos 2 x =1 1 + (y¢)2 = y × y¢¢

xy′′ + 0,5y′ = 0,25y

y¢¢ + ye2x = y¢

y¢¢ +12y = e4x + 7 y¢ y¢¢ + y¢ - xe2x = 6y

y¢¢ - 4ex sin x = 2y¢ - 2y y′′ + y - cos x = 0

y′′ + 4y = sin x

13.y = log2 (x − 4)

22

y = log2 (x − 4)

58

24.y = x3 + 3x2 + 2

25.y= (3 − x)e−x

[-1; 2]

[-3; -1]

[-2; 1] [-1; 3]

[-2; 1] [-1; 4] [-2; 1] [ 0; π/2] [-1; 2] [ 0; 3] [-5;-1]

[0;π] [-3;3]

[- π2 ; π2 ] [0; 3 ] [1;3]

[- 12 ;1] [0;2]

[-1;0]

[-1;3] [0;5]

1.y = xe− x44

x2 + 2x +1

5.y = x4 - 2x2 + 3

11.y = x2 ln x

13.y = (x -1)2 (x - 2)3

6.y = 3(x2 - 4)2

8.y = (x +1)e2x

14.y = (2x2 + 2x -3)e−2x

18.y = x + 1x

21.y = arctgx - 12 ln(1+ x2 )

23.y = 2x - 33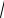x2

22.y =

24.y =

26.y =

28.y =

30.y =

x2 + x12

x3(x + 2)2

− x2

xe 2

2x2 - ln x

x - ln(1+ x2 )

1.y = ln(x2 + 4)

= æ1+ x ö4 3. y çè1- x ÷ø

5.y = x2 ln x

9.y = x3 + 4

x2

11.y = x − arctgx

x2

13.y = xe− 2

15.y = x2x+1

17.y = x + sin x

1

19. y = x2 -1

6.y = ex (x2 +1)

12.y = 2x - 32 ln(1+ x2 )

14.y = 2x ln 2x

16.y = exx

1

18.y = x2 +1

20. y = (x + 1) ln x