Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Запорожский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МАТЕМАТИКА 2Ч

.pdf

Скачиваний:

Добавлен:

07.02.2016

Размер:

476.22 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

21.	lim	cos3x - cos3 3x
			arctg 2 3x
	x→0
23.	lim		sin 3x + sin 2x

	x→0 arctg(x2 )+ 2x
25.	lim		x arcsin 3x
		cos2 2x -1
	x→0

27.lim arctg(x2 )- 3x x→0 sin 5x + sin 3x

29.	lim		cos3x - cos x

	x→0			arctg 2 3x
	1.2.14 Знайти границі
1.	lim	æ x + 3 ö2−3x
		ç			÷

	x→∞è x - 2 ø
3.	lim	æ		3x + 2			öx+2
		ç				÷
				3x -1
	x→∞è					ø
5.	lim	æ		2x - 3			ö2x+1
		ç				÷
				2x +1
	x→∞è					ø
7.	lim	æ		3x -1 ö2−x
		ç				÷
				3x - 3
	x→∞è					ø
9.	lim	æ		2x + 5			ö− x
		ç				÷
				2x -1
	x→∞è					ø
11.	lim	æ		4x + 3			ö2−3x
		ç				÷
				4x -1
	x→∞è					ø
13.	lim	æ		7x + 2 öx+2
		ç					÷
				7x - 3
	x→∞è					ø

22. lim

x→0

24. lim

x→0

26. lim

x→0

28. lim

x→0

30. lim

x→0

arctg x ×sin 4x

cos3x - cos x

1- cos2 3x x arctg 2x x × arcsin x

1- 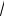cos x tg3x - sin x

arctg3x

x × arctg 2x

cos x - cos3x

2.	æ	2x -1			ö3x−1
	limç				÷
		2x + 3
	x→∞è				ø
4.	æ	4x -1			ö2−x
	limç				÷
		4x + 2
	x→∞è				ø
6.	æ x -1 ö2x−1
	limç		÷

	x→∞è x - 3 ø
8.	æ	5x +1 ö1−x
	limç				÷
		5x + 3
	x→∞è				ø
10.	æ x - 4 ö3x+2
	limç			÷

	x→∞è x + 2 ø
12.	æ	3x - 3			ö4x−3
	limç				÷
		3x + 2
	x→∞è				ø
14.	æ	2x + 6 ö2−x
	limç				÷
		2x - 3
	x→∞è				ø

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

15.	æ x + 5 ö3−2x
	limç		÷

	x→∞è x + 2 ø
17.	æ x + 8 ö−3x
	limç			÷

	x→∞è x + 4 ø
19.	æ	2x			ö− x
	limç				÷
		2x +1
	x→∞è				ø
21.	æ	2x + 5				ö5x
	limç					÷
		2x -1
	x→∞è				ø
23.	æ	3x + 2				ö− x
	limç				÷
		3x - 4
	x→∞è				ø
25.	æ	3x - 2				ö3x+4
	limç				÷
		3x - 5
	x→∞è				ø
27.	æ	5x -1				ö−3x
	limç					÷
		5x + 2
	x→∞è				ø
29.	æ	2x +1				ö3−2x
	limç					÷
		2x - 6
	x→∞è				ø

1.2.15 Знайти границі

1.lim (1+ 2x2 )x2

x→0

3.lim (1+ 2x3 )x4+3x3

x→0

						1
5.		æ		x	2	ö
							x2
	lim	ç1	-			÷

		ç		2		÷
	x→0è					ø

16.	æ	2x - 5			ö4x+3
	limç				÷
	limç	2x +1			÷
	x→∞è	2x +1			ø
18.	æ	3x			ö2x−4
	limç				÷
	limç	3x + 2			÷
	x→∞è	3x + 2			ø
20.	æ	x		ö2−3x
	limç		÷
	limç		÷
	x→∞è x - 2		ø
22.	æ	x +1 ö			2x−1
	limç			÷
	limç			÷
	x→∞è x + 2		ø
24.	æ	2x + 4			ö3x−1
	limç				÷
	limç	2x -1			÷
	x→∞è	2x -1			ø
26.	æ	3x			ö1−3x
	limç				÷
	limç	3x + 4			÷
	x→∞è	3x + 4			ø
28.	æ	6x +1			ö1−3x
	limç				÷
	limç	6x + 2			÷
	x→∞è	6x + 2			ø
30.	æ	7x -1			ö3x
	limç				÷
	limç	7x + 2			÷
	x→∞è	7x + 2			ø

2.lim (1− 3x2 )x2

x→0

	lim (1+ 3x3 )						2
4.	lim (1+ 3x3 )					x5−2 x3
	x→0
	æ		x ö				2
6.	æ	-	x ö		x2		+2x
	limç1			÷
	limç1			÷
	x→0è		4 ø

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

				2
7.		æ	3 + 2x ö
7.	lim	æ	3 + 2x ö				x
		ç			÷
		ç	3		÷
	x→0è		3	ø
				3
9.	lim (1+ 3x2 )					2 x2
	x→0
		æ		2 ö				5
11.		æ	3 - x	2 ö			x4	−3x2
	lim	ç			÷
	lim	ç			÷
		ç	3	÷
	x→0è		3	ø
								3

13.limæç 2 + 3x2 ö÷5x2

→ç 2 ÷

x0è ø

	lim (1− 3x3 )		5
15.	lim (1− 3x3 )			x4 +x3
	x→0
			1
17.	æ	4 + 2x ö
17.	æ	4 + 2x ö			x2	−x
	limç			÷
	limç	4		÷
	x→0è	4	ø
			1

19.limæç 2 - 3x2 ö÷ x2

→ç 2 ÷

x0è ø

						2
21.		æ		x	3	ö
							x3
	lim	ç1	-			÷

		ç		3		÷
	x→0è					ø
						1

23.limæç 4 + x3 ö÷ x3

ç4 ÷

x0è ø→

					2
25.		æ	5	- x	3 ö
							x3
	lim	ç				÷

		ç		5	÷
	x→0è				ø

				1
8.		æ	4 + x ö−
	lim				x
		ç		÷
			4
	x→0è			ø

10.limæç 2 + 3x2 ö÷ x4+2x2

→ç 2 ÷

x0è ø

				1
12.		æ	4 - 5x ö
12.	lim	æ	4 - 5x ö		x2	−x
		ç		÷
		ç	4	÷
	x→0è		4	ø
						4

14.limæç 5 + 2x2 ö÷ x2

→ç 5 ÷

x0è ø

16.limæç 2 + 3x3 ö÷ x3

ç2 ÷

è øx→0

					2
18.	æ 3 + 5x ö
18.	æ 3 + 5x ö						x
	limç				÷
	limç	3			÷
	x→0è	3			ø
	æ		x2		ö			2
20.	æ		x2		ö	x3		+x2
	ç	+			÷
	ç				÷
	limç1		3		÷
	x→0è		3		ø
					1
22.	æ		x	4	ö
	æ			4	ö	x4
	limç1	+			÷
	limç1	+			÷
	ç		4		÷
	x→0è		4		ø
								4

24.limæç 3 - 5x2 ö÷ x2

→ç 3 ÷

x0è ø

26.limæç 7 - 2x2 ö÷ x2

→ç 7 ÷

x0è ø

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

27.limæç 7 + x3 ö÷ x3 x 0çè 7 ÷ø→

29.limæç 5 - 2x3 ö÷ x3−x4

→ç 5 ÷

x0è ø

1.2.16 Знайти границі

	æ	2x +1ö2x+3
1.	lim ç				÷
		3x - 5
	x→∞è				ø
	æ	5x -1 öx+4
3.	lim ç				÷
		3x + 4
	x→∞è				ø
	æ	x - 5 ö3x
5.	lim ç				÷
		4x + 2
	x→∞è				ø
	æ	1+ x				ö5x
7.	lim ç					÷
		2 + 7x
	x→∞è				ø
	æ	1- 2x ö−4x
9.	lim ç			÷

	x→∞è	2 - x ø
	æ	5x + 4 ö2x
11.	lim ç				÷
		x + 6
	x→∞è				ø
	æ	x + 4 ö−4x
13.	lim ç				÷
		3x - 7
	x→∞è				ø
	æ	6x - 5 ö2x+1
15.	lim ç				÷
		x + 4
	x→∞è				ø
	æ	x + 3 ö5x
17.	lim ç		÷

	x→∞è	3x -1ø

28.	lim	æ
	lim	ç
		ç
	x→0è
30.	lim	æ
	lim	ç
		ç
	x→0è

		1
5 + 2x	2	ö−
			x2
		÷

5		÷
		ø
		1
2 - 5x	3	ö−
			x3
		÷

2		÷
		ø

	æ	3x -1ö1−2x
2.	lim ç		÷

	x→∞è	x + 4 ø
	æ	3x +1ö2x
4.	lim ç				÷
		4x -1
	x→∞è				ø
	æ	x + 3 ö−2x
6.	lim ç						÷
		9x - 7
	x→∞è				ø
	æ	2x - 5					ö−3x
8.	lim ç					÷
		3x +1
	x→∞è				ø
	æ	2 - x ö−6x
10.	lim ç				÷
		3 - 4x
	x→∞è				ø
	æ	x +1					ö2x
12.	lim ç					÷
		4x - 5
	x→∞è				ø
	æ	x - 3 ö−3x
14.	lim ç			÷

	x→∞è	3x +1ø
	æ	x + 2					ö4x
16.	lim ç					÷
		3x + 7
	x→∞è				ø
	æ	3x + 4					öx−1
18.	lim ç					÷
		x - 6
	x→∞è				ø

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

19.	lim	æ	x + 5				ö − 2 x
		ç					÷
		ç	3 x	- 4			÷
	x → ∞ è		3 x	- 4			ø
	æ	x + 4 öx+3
21.	lim ç			÷
21.	lim ç	5x - 4		÷
	x→∞è	5x - 4		ø
	æ	2x + 4 ö2−x
23.	lim ç					÷
23.	lim ç	x - 3				÷
	x→∞è	x - 3		ø
	æ	2x -1ö−4x
25	lim ç			÷
25	lim ç	x +1		÷
	x→∞è	x +1		ø
	æ	5x + 7 öx+4
27.	lim ç				÷
27.	lim ç	3x - 2			÷
	x→∞è	3x - 2		ø
	æ	2x +1ö1−3x
29.	lim ç			÷
29.	lim ç	4x -1		÷
	x→∞è	4x -1		ø

1.2.17 Знайти границі

1.	lim	ln(1		+ sin 2x)


	x→0		3 x +1 -1
3.	lim	ln(1		- 7x)

	x→0		23x -1
5.	lim	ln(1		+ 4x)
		e	5x	- e	3x
	x→0
7.	lim		ex2 - ex

	x→0 ln(1+ x2 - x)
9.	lim	ln(1+ 3x2 )
		(1+ x2 )5 -1
	x→0


	æ		x - 3 ö					2x
20.	lim ç					÷

	x→∞è		4x + 3ø
	æ		2x + 3 ö−x+1
22.	lim ç						÷

	x→∞è		7x - 5 ø
	æ		3x +1öx−1
24.	lim ç				÷

	x→∞è		2x -1ø
	æ		x +1 öx
26.	lim ç			÷

	x →∞è		2x + 3 ø
	æ		x +1 ö2x+1
28.	lim ç						÷

	x→∞è	3x + 2 ø						2−3x
	æ		2x - 3 ö
30.	lim ç					÷

	x→∞è		5x - 5 ø

2.	lim		ex2 -1
2.	lim
	x→0 ln(1+ 2x2 )
4.	lim	e3x - e−2x
4.	lim
	x→0	1+ 2x -1
6.	lim		3x2 -1
6.	lim
	x→0 3 1+ x2 -1
8.	lim	5x - 3x
8.	lim
	x→0	5 1+ x -1
10.	lim	(1+ 2x)4 -1
10.	lim	ln(1+ 5x)
	x→0	ln(1+ 5x)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

11.

lim

e2x − ex

x→0

3 1+ x −1

−1

13.

lim

1+ x2

x→0 ln(1+ sin 2 x)

15.

lim

ex2 −1

x→0 3 1+ 2x2 −1

17.

lim

ex3 −1

x→0 ln(1+ 3x3 )

−1

19.

lim

1+ x sin x

1− ex2

x→0

21.

lim

ln(1+ xsin x)

x→0

1− 2x2

23.

lim

e−x2 −1

x→0 5 1− x2 −1

25.

lim

esin 2 x −1

x→0 ln(1+ arctg 2 2x)

27.

lim

earcsin x −1

x→0

5 1+ x −1

29.

lim

1− e−x3

x→0

4 1+ 2x −1

1.2.18 Знайти границі

lim

sin(x − π 3)

1− 2cos x

x→π

12.

lim

(1+

tgx)

5 1+ x −1

x→0

14.

lim

5x2 −1

x→0 5 1+ x2 −1

16.

lim

1− 2x

x→0 ln(1+ 2x)

18.

lim

1+ 2x3

−1

e3x3 −1

x→0

20.

lim

ex2 −1

sin 2 x

x→0

22.

lim

1+ 2x2

−1

ln(1− 3x2 )

x→0

24.

lim

4 1+ x2 −1

ln(1+ 3x2 )

x→0

26.

lim

5x − 22x

x→0 arctg2x − 7x

28.

lim

2x2 −1

x→0 ln(1+ 3x2 )

30.

lim

3x3 −1

x→0 arcsin x3

2.	lim	2	cos x −1
		1− tg 2 x
	x→π 4

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

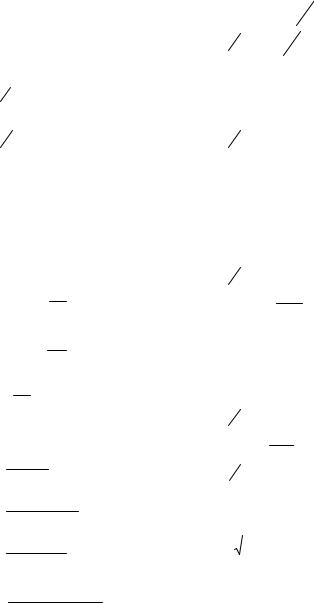
3.	lim	sin (m x)

	x→π sin(n x)
5.						æ π		ö
	lim tg2x ×tgç						4	- x÷
	x→π 4				è			ø
7.	lim		1− sin x
				π - 2x
	x→π 2
9.	lim		sin(x + 2)
					x3 + 8
	x→−2
11.	lim		tg(x + 2)
				x2 - 4
	x→−2
13.	lim	sin			3(x - 2)
		2			- 3x + 2
	x→2 x

15.lim(7 − 6x)3x−3

x→1

17.lim (3x − 8)x−3

x→3

19.lim x x−1

x→1

21.	lim
	lim
	x→1
23.	lim
	x→3
25.	lim
	x→1
27.	lim
	x→π

cos π2x

1- x

sin(x - 3)

x2 - 4x + 3 1+ cosπx

tg 2πx

cos5x - cos3x

sin 2 x

4.	lim				tgx - tg	π	6

					x -π
	x→π		6			6
6.	lim(1- x)tg πx
	x→1			2
8.	lim			1− sin 2x
					π - 4x
	x→π		4
10.	lim		x3 - 64

	x→4 tg(x - 4)
12.	lim	sin(x - 3)

	x→3			x3 - 27
14.	lim			1− 2sin x
					cos3x
	x→π		6
					2x

16.lim (3x − 5)x2 −4

x→2

18.	lim(1+ sin πx)ctgπx
18.	x→1
		æ	x		π	ö
20.	lim ç		x	-	π	÷
	lim ç			-		÷
	x→π	ç				÷
	x→π	2è ctgx			2cos x ø
				1

22.lim (tgx)1−tgx

x→π 4


24.	lim	1+ cos3x
				sin 2 7x
	x→π
26.	lim			x2 − x + 1 −1
				tgπx
	x→1
28.	lim	2x -16
			sin πx
	x→4

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com


29.	lim	sin 5x	30.	lim		1- sin x
	lim	tg3x		lim
	x→π	tg3x		x→π	2 æ π		ö2
					ç		- x÷
					è 2		ø

2.НЕПЕРЕРВНІСТЬ ФУНКЦІЇ

2.1 Аудиторні завдання

Завдання 1. Визначити область існування функції:

5x - 3

б) y = arccos

x - 3

- lg(3x + 6)

а) y = arcsin

4x2 -1

Відповідь: xÎ

é 1

ú.

Відповідь: xÎ(- 2; 8 ]

ë 2

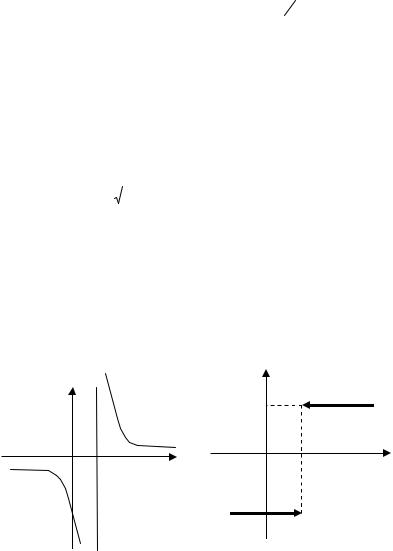
Завдання 2. Дослідити на неперервність функції

а) y =

б) y =

x -1

x - 2

x -1

y =

x − 2

y =

x -1

x=2

-1

Рисунок 2.1

Рисунок 2.2

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

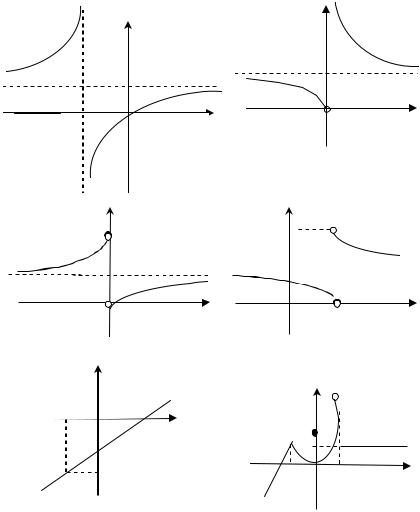
Завдання 3. Дослідити функцію f (x) на неперервність вказати точки розриву і побудувати графік

а) y =

г)

y =

;

x + 2

Відповідь:

x =1 точка розриву

1 + 5

1−x

другого роду

Відповідь:

x =1 точка

розриву

першого роду

-1

при

x ¹ -1

y =

б) y = 2

;

í x +1

д)

при

x = -1

î- 2

Відповідь:			x = 0 точка	розриву
другого роду
в) y =	1		;
в) y =		1	;
	1 + 2	x
Відповідь:			x = 0 точка	розриву
першого роду

Відповідь: функція неперервна

	ìx + 2,	x < -1
е)	ï	-1 £ x <1,5
е)	y = íx2 ,	-1 £ x <1,5
	ï	x ³1,5
	î1	x ³1,5

Відповідь: функція неперервна в т. х= -1; х=1,5 точка розриву першого роду

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

б)

у=1

-2	0	х	0	х
	0		0

в)

г)

y =

1/2

y=3/2

д)

е)

y = x2

-1

y=x+2

y=1

-2

1,5

-1

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.07.2019125.44 Кб4Массовые репрессии и политические процессы 20-х....doc
#
07.02.2016588.27 Кб13матанчик 4 идз.pdf
#
07.02.20161.16 Mб9математика 1227.pdf
#
07.02.2016459.93 Кб7математика 1229.pdf
#
07.02.2016530.12 Кб7математика 1874.pdf
#
07.02.2016476.22 Кб8МАТЕМАТИКА 2Ч.pdf
#
07.02.2016309.25 Кб16математика 3700.pdf
#
07.02.2016594.89 Кб716математика 3701.pdf
#
07.02.20163.15 Mб15Математика задания(30 вариантов).doc
#
07.02.20165.01 Mб110Матеріалознавство.pdf
#
07.02.20163.31 Mб21материаловедение.pdf