
математика 3701
.pdf51
6.2 Система неперервних ВВ (Х, Y)
Системою неперервних ВВ (Х,Y) називають систему випадкових величин, складові Х, Y якої неперервні.
Якщо функція спільного розподілу F(х, у) неперервна і має другу мішану похідну по х і у, то цю похідну називають щільністю спільного розподілу і позначають f(х, у). Таким чином,
|
f (x, y) = |
∂ 2 F |
|
|
|
∂x∂y |
|
||
|
|
|
||
Щільність спільного розподілу f (x, y) має такі властивості: |
||||
|
|
|
∞ |
∞ |
а) f(x,y) ≥ 0; |
|
|
б) ò |
ò f (x, y) dx dy =1. |
−∞ −∞
Знаючи щільність розподілу, можна знайти інтегральну функцію розподілу за формулою:
x y
F(x, y) = ò ò f (x, y) dx dy.
−∞ −∞
Імовірність попадання випадкової точки (Х, Y) в довільну область D знаходиться за формулою:
P((X ,Y) D) = òò f (x, y) dx dy.
D
Щільності розподілу компонент X, Y, що входять в систему (Х, Y), виражаються через щільність спільного розподілу системи формулами:
∞ |
∞ |
f1 (x) = ò f (x, y) dy ; |
f2 ( y) = ò f (x, y) dx |
−∞ |
−∞ |
Випадкові величини Х і Y називаються незалежними, тоді і тільки тоді, коли: f(x, y) = f1(x) f2(y).
6.3 Числові характеристики двовимірних випадкових величин
1. Математичним сподіванням двовимірної ВВ (X,Y) називається впорядкована пара чисел (М(Х), М(Y)).
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

52
Для дискретної ВВ (X, Y):
n m |
n |
m |
M (X ) = mX = å åxi pij , |
M (Y ) = mY = å å y j pij |
|
i=1 j=1 |
i=1 |
j=1 |
Для неперервної ВВ (X, Y): |
|
|
∞ ∞ |
∞ ∞ |
|
M (X ) = mX = ò ò x × f (x, y) dx dy, |
M (Y) = mY = ò ò y × f (x, y) dx dy. |
|
−∞ −∞ |
−∞ −∞ |
|
Математичне сподівання (mX, mY) – координати середньої точки, щодо якої розкидані випадкові точки (X, Y). (mX, mY) іноді називають центром розсіювання.
2. Дисперсією двовимірної ВВ (X,Y) називається впорядкована пара чисел (D(Х), D(Y)).
Для дискретної ВВ (X, Y):
n m |
n |
m |
D(X ) = å å(xi - mX )2 pij , D(Y)= å å(y j - mY )2 pij . |
||
i=1 j=1 |
i=1 j =1 |
|
Для неперервної ВВ (X, Y): |
|
|
∞ ∞ |
∞ |
∞ |
D(X ) = ò ò(x - mX )2 f (x, y) dx dy, |
D(Y) = ò ò(y - mY )2 f (x, y) dxdy |
|
−∞ −∞ |
−∞ −∞ |
|
Дисперсія (D(Х), D(Y)) показує наскільки хмара точок (X,Y) розкидана в напрямку осей Ох і Оy.
3. |
Середнє квадратичне відхилення двовимірної ВВ (X,Y) |
||||
обчислюють за формулами: |
|||||
|
σ х = |
|
та σ y = |
|
|
|
D( X ) |
D(Y ) |
|||
4. |
Початковим моментом ν К,S порядку k + s системи ВВ (X,Y) |
||||
називають математичне сподівання добутку XKYS: ν К,S = М[XKYS].
Зокрема, ν 1,0 = М(Х), ν 0,1 = М(Y). 5. Центральним моментом
називають математичне сподівання добутку відхилень відповідно до k – го і s – го ступенів: μК,S = М{[X–М(Х)]K [Y–М(Y)]S}. Зокрема,
μ1,0 = 0, μ0,1 = 0, μ2,0 = D(X), μ0,2 =D(Y).
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

53
6.4 Умовні закони розподілу
Якщо ВВ Х і Y, що утворюють двовимірну ВВ (Х, Y) залежні, для характеристики цієї залежності вводять поняття умовного розподілу.
Умовним законом розподілу випадкової величини, що входить до системи, називається її закон розподілу, обчислений за умови, що інша випадкова величина прийняла певне значення. Наприклад, умовним законом розподілу ВВ Х, що входить у систему ВВ (Х, Y), називається її закон розподілу, знайдений за умови, що друга ВВ Y прийняла певне значення (або потрапила в певний інтервал). Для залежних ДВВ Х і Y умовні ймовірності обчислюються за формулами:
P( X = x /Y = y |
j |
) = |
P(X = xi;Y = y j ) |
або |
P(x / y |
j |
) = |
P(xi ; y j ) |
, |
|
|
||||||||
i |
|
P(Y = y j ) |
|
i |
|
P(y j ) |
|
||
|
|
|
|
|
|
|
|
P(Y = y j / X = xi ) = |
P(X = xi ;Y = y j ) |
|
P(X = xi ) |
||
|
n
åP(xi / y j ) =1,
i=1
або P(y j / xi ) = P(xi ; y j ) , P(xi )
m
åP(y j / xi ) =1.
j=1
Цю властивість умовних розподілів використовують для контролю обчислень. Якщо безумовні і умовні ймовірності (Р(хi) і P(xi / yj); Р(yj) і P(yj / xi)) відрізняються, то величини Х і Y залежні, а якщо збігаються – незалежні.
Для залежних НВВ Х і Y умовні щільності розподілу (або щільності ймовірності умовного розподілу) випадкових величин Х і Y, що входять у систему, позначаються φ(x / y) – умовна щільність
розподілу випадкової величини Х за умови, що випадкова величина Y = y і ϕ(y / x) – умовна щільність розподілу випадкової величини Y
за умови, що випадкова величина Х = х і визначається як:
φ(x / y) = |
f (x, y) |
, f2 ( y) ¹ 0; |
ϕ(y / x) = |
f (x, y) |
, f1 (x) ¹ 0 |
|
f2 ( y) |
f1 (x) |
|||||
|
|
|
|
Для незалежних випадкових величин φ(x / y) = f1(x) і ϕ(y / x) = f2(y),
тому f(x,y) = f1(x) f2(y).
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
54
6.4.1Числові характеристики умовних розподілів
1.Умовним математичним сподіванням ВВ Х при Y = y, де y – одне з можливих значень ВВ Y, називається:
|
n |
для дискретної ВВ |
M (X / Y = y) = åxi p(xi / y) , |
|
i=1 |
|
∞ |
для неперервної ВВ |
M (X / Y = y) = ò xφ(x / y) dx . |
|
−∞ |
Умовне математичне сподівання М(Х / y) є функцією y, яку називають функцією регресії Х на Y.
Аналогічно визначається умовне математичне сподівання М(Y / х), що є функцією х і називається функція регресії Y на Х.
2. Кореляційний момент KXY (коваріація) системи ВВ (X, Y) називається величина
KXY = coν (X ,Y ) = М[(Х – mХ) (Y – mY)].
Для дискретної ВВ (X, Y):
n m |
n |
m |
K XY = å å |
(xi - mX )(y j - mY ) pij = å åxi y j pij - mX mY . |
|
i=1 j=1 |
i=1 |
j=1 |
Для неперервної ВВ (X, Y): |
|
|
∞ ∞ |
∞ |
∞ |
KXY = ò ò (x - mX )( y - mY ) × f (x, y) dx dy = ò òx y f (x, y) dx dy - mX mY .
−∞ −∞ |
−∞ −∞ |
|
|
ВВ X і Y називаються некорельованими, якщо їх KXY = 0. |
|||
Властивості коваріації: а) KXY |
= КYX; |
б) |
соν (X + a,Y) = |
= соν (X ,Y + b) = соν (X + a,Y + b) |
= соν ( X ,Y) ; |
в) |
якщо випадкові |
величини X і Y незалежні, то KXY = 0; якщо KXY ¹ 0, то випадкові величини X і Y залежні; в) coν (cX ,Y ) = c ×coν (X ,Y) = coν (X , cY ) ;
г) D(X ± Y) = D(X) + D(Y) ± 2 KXY; д) | KXY | ≤ σX σY.
3. Безрозмірною характеристикою зв'язку між ВВ X і Y є
коефіцієнт кореляції |
|
|
|
|
|
coν (X ,Y) |
|
|
|
|
æ |
X - mX |
|
ö |
|
|
K XY |
||
|
ç |
|
Y - mY ÷ |
|
|
||||
rXY |
= coν ç |
|
, |
|
÷ |
= |
|
= |
|
σ X |
|
σ X σY |
σ X σY |
||||||
|
è |
|
σ Y ø |
|
|
||||
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

55
Він характеризує ступінь тісноти лінійного зв'язку між випадковими величинами: якщо | rXY | → 1, то зв'язок сильніше; якщо | rXY | → 0, то зв'язок слабкіше. Властивості коефіцієнта кореляції:
а) | rXY | ≤ 1;
б) для незалежних ВВ rXY = 0;
в) якщо ВВ X і Y пов'язані лінійною функціональною залежністю
Y = аX + b, а ¹ 0, то | rXY | = 1, причому rXY = 1 при а> 0 і rXY = –1 при
а <0 і навпаки.
Приклад 39.Дана двовимірна ВВ (Х, Y). Знайти: а) граничні закони ВВ Х та Y; б) умовний закон ВВ Х при y = 2,9; в) числові характеристики mX, mY, σX, σY, rXY.
Y \ Х |
1,7 |
1,8 |
1,9 |
2,0 |
|
|||||
2,7 |
0,01 |
0,02 |
0,04 |
0,04 |
|
|||||
2,8 |
0,01 |
0,22 |
0,13 |
0,4 |
|
|||||
2,9 |
0,05 |
0,125 |
0,12 |
0,105 |
|
|||||
3,0 |
0,015 |
0,035 |
0,025 |
0,015 |
|
|||||
Розв’язування. а) запишемо граничні закони ВВ Х та Y: |
||||||||||
Х |
|
1,7 |
|
1,8 |
1,9 |
|
2,0 |
|
||
р |
|
0,085 |
|
0,4 |
0,315 |
|
0,2 |
|
||
|
|
|
|
|
|
|
|
|||
Y |
|
2,7 |
|
2,8 |
|
2,9 |
3,0 |
|
||
р |
|
0,11 |
|
0,4 |
|
0,4 |
0,09 |
|
||
б) умовний закон ВВ Х при y = 2,9. Знайдемо умовні
ймовірності за формулою: |
|
|
|
|
|
|
|
|
|
||||||
|
P(x / y = y |
k |
) = |
|
P(xi ; yk ) |
. З таблиці закону розподілу для ВВ Y |
|||||||||
|
|
||||||||||||||
|
i |
|
|
|
P( yk ) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
маємо, що р(y = 2,9) = 0,4. Тоді р(х1/ y = 2,9) = |
0,05/0,4 = 0,125; |
||||||||||||||
р(х2/ y = 2,9) |
= 0,125/0,4 = 0,3125; |
р(х3/ y = 2,9) |
= 0,12/0,4 = 0,3; |
||||||||||||
р(х4/ y = 2,9) = 0,105/0,4 = 0,2625. |
|
|
|
|
|
|
|||||||||
|
|
Х |
|
|
1,7 |
|
1,8 |
|
1,9 |
|
2,0 |
|
|
||
|
Р(Х/ y=2,9) |
|
0,085 |
|
0,4 |
|
0,315 |
|
0,2 |
|
|
||||
в) знайдемо числові характеристики mX, mY, σX, σY, rXY.
Математичне сподівання ВВ Х:
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

56
4
mX = åxi pi =1,7 × 0,085 +1,8 × 0,4 +1,9 × 0,315 + 2 × 0,2 =1,863
i=1
Математичне сподівання ВВ Y :
4
mY = å y j p j = 2,7 × 0,11 + 2,8 × 0,4 + 2,9 × 0,4 + 3 × 0,09 = 2,847
j=1
Дисперсія ВВ Х:
4
DX = åxi2 pi - (mX )2 =1,72 × 0,085 +1,82 × 0,4 + 1,92 × 0,315 + 22 × 0,2 -
i=1
-(1,863)2 = 0,009231
Дисперсія ВВ Y :
4
DY = å y2j p j - (mY )2 = 2,72 × 0,11 + 2,82 × 0,4 + 2,92 × 0,4 + 32 × 0,09 -
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- (2,847)2 = 0,006591 |
|
|
|
|
|
|
|
|
|
||||||||||||
Середнє квадратичне відхилення ВВ Х: |
|
|
|
|
|
||||||||||||||||
|
σ X |
= |
|
|
|
|
|
= |
|
|
|
|
» 0,096 . |
|
|
|
|
|
|
||
|
DX |
|
0,009231 |
|
|
|
|
|
|||||||||||||
Середнє квадратичне відхилення ВВ Y: |
|
|
|
|
|
||||||||||||||||
|
σY |
= |
|
|
|
= |
|
|
» 0,0812 . |
|
|
|
|
|
|||||||
DY |
0,006591 |
|
|
|
|
|
|||||||||||||||
|
Закон розподілу ВВ (ХY): |
|
|
|
|
|
|
|
|
||||||||||||
|
ХY |
|
4,59 |
|
|
|
4,76 |
|
4,93 |
|
|
5,1 |
|
4,86 |
5,04 |
5,22 |
5,4 |
||||
|
р |
|
0,01 |
|
|
|
0,01 |
|
0,05 |
|
|
0,015 |
|
0,02 |
0,22 |
0,125 |
0,035 |
||||
|
ХY |
|
5,13 |
|
|
5,32 |
5,51 |
|
5,7 |
|
5,4 |
5,6 |
5,8 |
6,0 |
|||||||
|
р |
|
0,04 |
|
|
0,13 |
0,12 |
|
0,025 |
|
0,04 |
0,04 |
0,105 |
0,015 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдемо математичне сподівання ВВ (ХY):
M (XY ) = å(xy)i pi = 4,59 × 0,01 + 4,76 × 0,01 + 4,93 × 0,05 + 5,1× 0,015 +
i
+4,86 × 0,02 + 5,04 × 0,22 + 5,22 × 0,125 + 5,4 × 0,035 + 5,13 × 0,04 +
+5,32 × 0,13 + 5,51× 0,12 + 5,7 × 0,025 + 5,4 × 0,04 + 5,6 × 0,04 +
+5,8 × 0,105 + 6,0 × 0,015 = 5,3035
Знайдемо коефіцієнт кореляції за формулою:
r = |
KXY |
= |
M (XY ) - M (X ) × M (Y) |
= |
5,3035 -1,863 × 2,847 |
» -0,059 |
|
|
|
||||
XY |
σ XσY |
|
σ XσY |
0,096 × 0,0812 |
|
|
|
|
|
||||
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

57
7. ЛІНІЙНА РЕГРЕСІЯ. ПРЯМІ ЛІНІЇ СЕРЕДНЬОКВАДРАТИЧНОЇ РЕГРЕСІЇ
Нехай залежні ВВ X і Y пов'язані лінійною функціональною залежністю Y g(х) = а X + b, де а і b – параметри, що підлягають визначенню. Частіше для їх знаходження застосовують метод найменших квадратів. Для цього треба розв’язати систему двох рівнянь:
ì |
n |
n |
|
ïα åxi + n × b = åyi |
|||
ï |
i=1 |
i=1 |
|
í |
n |
n |
n |
ïïα åxi2 + båxi = |
åxi yi |
||
î |
i=1 |
i=1 |
i=1 |
Функцію g(х) називають середньоквадратичною регресією Y
на Х.
Лінійна середньоквадратична регресія Y на Х має вигляд:
g(х) = mY + rXY (σY / σX) (X – mX),
де mX = M(X), mY = M(Y), σY = 
 D(Y ) , σX =
D(Y ) , σX = 
 D(X ) , rXY =
D(X ) , rXY =
=KXY/(σY σX). Коефіцієнт а = rXY (σY / σX) називають коефіцієнтом регресії Y на Х, b = mY – rXY (σY / σX) mX, а пряму: y – mY =
=rXY (σY / σX) (x – mX ) називають прямою середньоквадратичної регресії Y на Х.
Аналогічно, пряма середньоквадратичної регресії Х на Y
має вигляд: х – mX = rXY (σX / σY) (y – mY), де rXY (σX / σY) –
коефіцієнт регресії Х на Y. Якщо rXY = 1, то ВВ Y і Х пов'язані лінійною функціональною залежністю і обидві прямі регресії збігаються.
Якщо і функція регресії Х на Y М(Х / y) = φ (y), і функція регресії Y на Х М(Y / х) = ϕ (х) – лінійні, то ВВ Х і Y пов'язані
лінійної кореляційною залежністю. У цьому випадку графіки функцій регресії є прямі. Ці прямі збігаються з прямими середньоквадратичної регресії.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

58
Приклад 40. Задана щільність спільного розподілу ВВ (Х, Y):
|
ìC × x × y, |
(x, y) Î D, |
де D: ( y ³ 0, х + y £ 2,x ³ 1 ). |
||||
f (x, y) = í |
(x, y) Ï D |
||||||
|
î0, |
|
|
|
|
|
|
Знайти: а) сталу С; б) рівняння лінії регресії Y на Х. |
|
||||||
|
Розв’язування. а) сталу С знайдемо з властивості щільності |
||||||
спільного розподілу: |
|
|
|
|
|
|
|
∞ |
∞ |
2 |
2−х |
5 |
|
|
|
ò |
ò f (x, y) dxdy =1Þ Cò x dx ò |
|
|
||||
y dy = C × |
|
=1 |
Þ С = 4,8 . |
||||
24 |
|||||||
−∞ −∞ |
1 |
0 |
|
|
|
|
|
Тоді |
ì4,8× x× y, |
(x, y) Î D, |
|
|
|
|
|
f (x, y) = í |
(x, y) Ï D |
|
|
|
|
|
|
|
î0, |
|
|
|
|
|
|
б) знайдеморівняннялініїрегресії Y на Х: y – mY = rXY (σY / σX) (x – –mX ), де rXY = KXY / (σY σX); K XY = òòx y f (x, y) dx dy - mx my ;
|
|
|
|
|
|
|
|
D |
|
mX = òò x × f (x, y) dx dy , |
mY = òò y × f (x, y) dx dy ; |
||||||||
|
|
D |
|
D |
|
|
|||
D(X ) = òò x2 f (x, y) dx dy - (mX )2 , |
D(Y ) = òò y2 f (x, y) dx dy - (mY )2 |
||||||||
|
|
В |
|
|
|
D |
|||
σ х = |
|
, σ y = |
|
. |
Тоді |
|
|
|
|
D(X ) |
D(Y ) |
|
|
|
|||||
|
|
|
|
|
|
2 |
2−x |
|
|
mx |
= òò x × 4,8 x y dx dy = 4,8òx2 dx ò |
y dy = 1,28; |
|||||||
|
D |
1 |
0 |
|
|
||||
|
|
|
|
|
|
2 |
2−x |
|
|
my |
= òò y × 4,8 x y dx dy = 4,8òx dx ò |
y2 dy = 0,48; |
|||||||
|
|
D |
1 |
0 |
|
2−x |
|||
|
|
|
|
|
|
|
|
2 |
|
D(X ) = òòx2 × 4,8 x y dx dy - (1,28)2 = 4,8òx3 dx ò y dy -1,6384 = 0,0416;
D |
1 |
0 |
2 |
|
2−x |
D(Y ) = òò y2 4,8 x y dx dy - (0,48)2 = 4,8ò x dx ò y3 dy - 0,2304 = 54,0096
|
D |
1 |
|
0 |
|
||||
σ х = |
|
= |
|
≈ 0,204; σ y = |
|
= |
|
|
≈ 7,349; |
D(X ) |
0,0416 |
D(Y ) |
54,0096 |
||||||
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
59
2 2−x
K XY = òò x y ×4,8 x y dx dy -1,28×0,48 = 4,8ò x2 dx ò y 2 dy - 0,6144 = 0,0256;
D |
1 |
0 |
rXY = 0,0256 / (0,204 7,349) = 0,02. Підставимо знайдені значення в рівняння лінії регресії: y – 0,48 = 0,02 7,349/0,204 (x – 1,28). Рівняння
регресії Y на X матиме вигляд : 0,72 x – y – 0,4416 = 0.
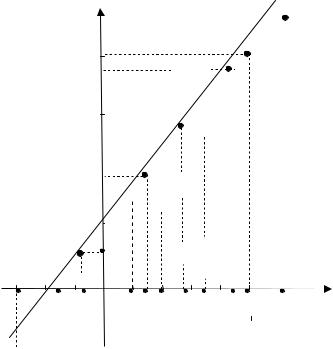
Приклад 41. За незгрупованими даними xi і yj (і = 1,2, ..., 10) результатів досліджень ВВ Х і Y скласти вибіркове рівняння прямої лінії регресії Y на X. В системі координат ХОY побудувати графік прямої лінії регресії та показати результати досліджень.
xi |
-3,0 |
-0,7 |
0,9 |
1,3 |
2,0 |
2,8 |
3,6 |
4,5 |
4,8 |
5,9 |
yj |
-2,1 |
1,4 |
2,9 |
3,7 |
4,1 |
5,7 |
6,4 |
7,3 |
7,5 |
8,3 |
Розв'язування. Рівняння прямої лінії регресії y = а х + b, де коефіцієнти а і b знайдемо за методом найменших квадратів за допомогою системи двох рівнянь:
ì |
n |
|
n |
|
ïα åxi + n ×b = å yi |
|
|||
ï |
i=1 |
n |
i=1 |
Знайдемо суми, що входять до |
í |
n |
n |
||
ïïα åxi2 + bå xi = åxi yi |
|
|||
î |
i=1 |
i=1 |
i=1 |
|
системи:
10
åxi = -3,0 + (-0,7) + 0,9 +1,3 + 2,0 + 2,8 + 3,6 + 4,5 + 4,8 + 5,9 = 22,1
i=1
10
å yi = -2,1+1,4 + 2,9 + 3,7 + 4,1+ 5,7 + 6,4 + 7,3 + 7,5 + 8,3 =45,2
i=1
10
åxi2 = (-3,0)2 + (-0,7)2 + 0,92 + 1,32 + (2,0)2 + 2,82 + 3,62 + 4,52 + 4,82 +
i=1
+ 5,92 =114,89
10
åxi yi = (-3,0)×(-2,1) + (-0,7) ×1,4 + 0,9×2,9 +1,3×3,7 + 2,0×4,1+ 2,8×5,7 +
i=1
+3,6×6,4 + 4,5×7,3+ 4,8×7,5 + 5,9×8,3 = 177,76
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
Одержимо систему двох лінійних рівнянь: |
|
|
|||||||||||||||||||
ì22,1 ×α |
+10 × b = 45,2 |
|
. Розв’яжемо систему за формулами |
||||||||||||||||||
í |
|
|
|
|
|
|
|
|
22,1× b =177,76 |
||||||||||||
î114,89 ×α + |
|
|
|
|
|||||||||||||||||
Крамера: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
D = |
|
|
22,1 |
|
10 |
|
|
= 22,12 |
-10 ×114,89 = -660,49 |
|
|
||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
114,89 |
22,1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
D |
= |
|
|
|
45,2 |
10 |
|
|
= 45,2 × 22,1 -10 ×177,76 = -778,68 |
|
|||||||||||
|
|
|
|||||||||||||||||||
α |
|
|
|
|
|
|
177,76 |
22,1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Db |
= |
|
22,1 |
|
45,2 |
|
= 22,1×177,76 - 45,2 ×114,89 = -1264,532 |
||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
114,89 |
177,76 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
α = |
Dα |
= |
- 778,68 |
»1,1789 |
b = Db = |
-1264,532 |
»1,9145 |
|||||||||
|
|
|
|
|
|
- 660,49 |
|||||||||||||||
|
|
|
|
|
|
|
|
D |
- 660,49 |
|
|
D |
|
||||||||
Отже, вибіркове рівняння лінії регресії має вигляд : y = 1,1789 х+ +1,9145.
y
8,9 




7,5
7,3
6,4 
5,7 
4,1

3,7
2,9

1,9
1,4
-3 |
-1,6 -0,7 0,9 1,3 2 2,8 3,6 4,5 4,8 5,9 |
x |
 -2,1
-2,1
Рисунок 7.1
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
