5.1.1 Математичні моделі цифрових автоматів

Ми вже розглядали закони функціонування, математичні моделі комбінаційних схем.

Розглянемо закон функціонування цифрових автоматів з погляду абстрактної теорії автоматів.

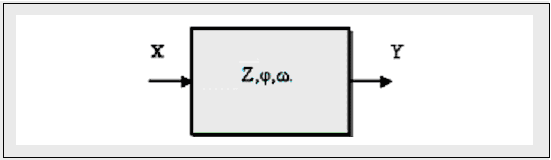
Рисунок 5.1 – Модель абстрактного цифрового автомата

Абстрактний автомат А − це узагальнене представлення опису функціонування моделі цифрової логічної системи у дискретному часі, яку визначають:

- множиною вхідних сигналів ;

- множиною вихідних сигналів ;

- множиною внутрішніх станів , включаючи й початковий, нульовий стан z₀;

- функцією переходіввідображення множини вхідних сигналівна множину внутрішніх станів;

- функцією виходів відображення множини вхідних сигналів і станівна множину вихідних сигналів.

Тоді, узагальнений закон або модель абстрактного автомата буде виглядати як математичний кортеж:

.

Автомат називають кінцевим, якщо кінцеві множини. Абстрактний автомат реалізує відображення множини слів вхідного алфавітуXна множину слів вихідного алфавітуY.

Узагальнений закон функціонування автомата не відтворює його поведінку в часі, а саме це питання є іноді основним при аналізі й синтезі цифрових систем. Серед багатьох спроб дати математичний опис поведінки автомата в часі, найбільше поширення одержали автомати Мілі й Мура.

Закон функціонування автомата Мілі:

Наступний стан автомата залежить від функції переходів φ, стану автомата на даний час z(t) і вхідних сигналів у цей момент часу. Вихідні сигнали залежать від функції виходів, вхідних сигналів x(t) і внутрішнього стану автомата, де− автоматний, дискретний час визначений тактовими імпульсами;z₀ − початковий, нульовий стан.

Закон функціонування автомата Мура:

Тобто, в автоматі Мура вихідні сигнали залежать тільки від стану автомата в цей момент і не залежать від вхідних сигналів.

5.1.2 Табличний спосіб завдання ца

Існує кілька способів завдання опису функціонування ЦА. Для завдання простих ЦА набули значне поширення табличні способи опису його функціонування у вигляді представлених таблиць 4.1 а,б: переходів, виходів автомата Мілі (а) та відмічених таблиць переходів автомата Мура (б).

Таблиця 5.1 – Приклади таблиць переходів, виходів та таблиці відмічених станів автомата

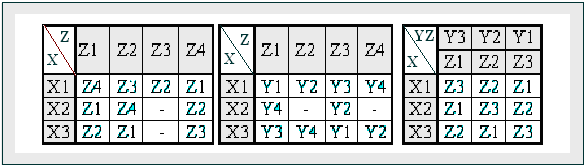
Автомат Мілі може не мати деяких станів і деяких вихідних сигналів. Такі автомати називаються частково повними. Якщо автомат має тільки один стан, то він називається тривіальним автоматом. Абстрактний автомат завжди має вхідний і вихіднийінформаційні канали й у кожний момент часу він перебуває в якомусь одному певному стані. Таблиця переходів надає опис переходу автомата із стануу стан, при умові надходження управління. Таблиця виходів вказує, який вихід стане при цьому активним. У відміченій таблиці стан і вихід суміщаються (для ЦА Мура).

5.1.3 Канонічний метод синтезу ца

Теоретичним обґрунтуванням структурного синтезу автоматів є теорема про структурну повноту.

Усяка система елементарних автоматів, що містить автомат Мура з нетривіальною пам’яттю, що володіє повною системою переходів і повною системою виходів, і яку-небудь функціонально повну систему елементів логічних функцій, є структурно повною.

Канонічний метод структурного синтезу припускає подання структурної й логічної схеми автомата у вигляді двох частин рисунку 13.1: пам’яті й комбінаційної схеми.

Пам’ять автомата складається з елементарних, повних автоматів Мура П₁,...,П_i…П_t.

Будь-який автомат Мура повинен мати повну систему переходів і повну систему виходів. Це означає, що для будь-якої пари станів автомата пам’яті знайдеться вхідний сигнал, що переключить його в інший стан. Повнота системи виходів автомата Мура полягає в тому, що кожному стану відповідає свій кодований сигнал на його виході. Інакше кажучи, у повному автоматі Мура його внутрішній стан ототожнюється з виходом, тобто, за його виходом можна визначити в якому стані він перебуває.

Загальна кількість елементів пам’яті Мура в автоматівизначається необхідною сукупністю всіх його внутрішніх станів, де 2 − основа бінарної системи числення. Так, наприклад, автомат, який має п’ять елементів пам’яті може мати 2⁵станів. Коди внутрішніх станів автомата (елементів пам’яті) визначаються бінарним числом із 5-ти розрядів.

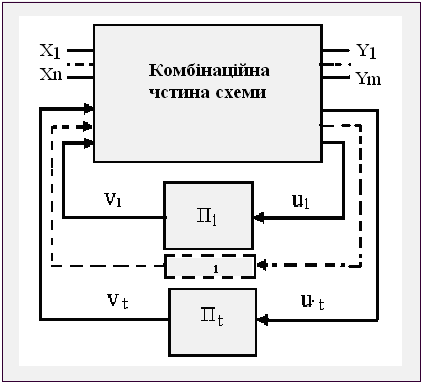
Рисунок 5.2 – Структура цифрового автомата Мілі

Так як, кожний стан автомата А визначається кодом станів елементів Мура, то, щоб перевести його, наприклад, зі стануу стан, необхідно переключити тригер третього розряду з 1 в 0. Ці переключення відбуваються під дією сигналів збудження, що надходять із комбінаційної частини автомата.

Результатом канонічного методу структурного синтезу є система логічних рівнянь математичного опису автомата.Ця модель відображає залежність вихідних сигналів автомата, у тому числі й сигналів переключення пам’яті, від сигналів вхідних змінних, у тому числі й сигналів із виходу елементів пам’яті.

Таким чином, при канонічному методі синтез автомата зводиться до вибору елементів пам’яті й побудови комбінаційної частини схеми, входами якої є сигнали вхідних змінних структурного автомата і сигнали оберненого зв’язку від елементів пам’яті, a виходами − сигнали на вихідних каналахі функцій переключення пам’яті. Автомат А можна задати наступною системою рівнянь:

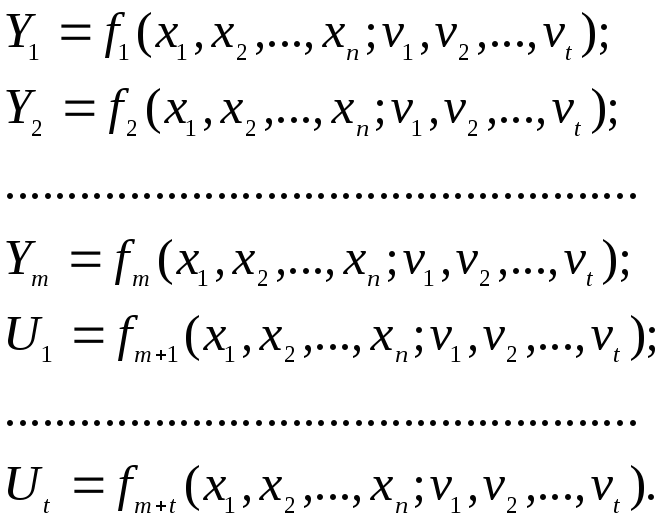
Для набуття практичних навичок проектування цифрових автоматів, розглянемо приклад застосування канонічного методу структурного синтезу логічної схеми.