4. Дисперсия функции случайных величин.

По определению дисперсии

.

Следовательно,

,

где

.

Здесь мы приведем расчетные формулы только для случая непрерывных случайных аргументов. Для функции одного случайного аргумента дисперсия выражается формулой

, (6.5)

где - математическое ожидание функции ; - плотность распределения величины .

Заметим, что при вычислении дисперсии бывает удобно пользоваться формулой

.

В таком случае формула (6.5) может быть заменена на следующую:

.

Таким образом, дисперсия функции случайных величин может быть определена как математическое ожидание квадрата этой функции минус квадрат ее математического ожидания.

Рассмотрим теперь теоремы о дисперсиях, которые играют очень большую роль в теории вероятностей и ее приложениях.

Теорема 6.3. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими:

.

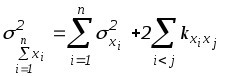Следствие 6.3. Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых:

.

Теорема 6.4. Дисперсия произведения двух независимых случайных величин вычисляется по формуле

.

5. Корреляционный момент функций случайных величин.

Согласно определению корреляционного момента двух случайных величин и , имеем:

.

Раскрывая скобки и применяя свойства математического ожидания, получим:

(6.6)

Рассмотрим две функции и случайной величины :

,

.

Согласно формуле (6.6)

,

отсюда

,

т. е. корреляционный момент двух функций случайных величин равен математическому ожиданию произведения этих функций минус произведение из математических ожиданий.

Рассмотрим основные свойства корреляционного момента и коэффициента корреляции.

Свойство 1. От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не меняются.

Свойство 2. Для любых случайных величин и абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий данных величин:

,

где , - средние квадратические отклонения величин и .

Следствие 6.5. Для любых случайных величин и абсолютная величина коэффициента корреляции не превосходит единицы:

.

ЗАДАЧИ

1. Через точку проведена наугад прямая. Найти плотность распределения расстояния этой прямой от начала координат.

Ответ:

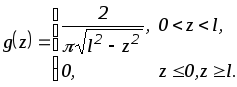
2. Дана плотность вероятности случайной величины (). Найти плотность вероятности случайной величины .

Ответ: .

3. Известны математическое ожидание и лисперсия случайной величины : , . Найти математическое ожидание и дисперсию случайной величины .

Ответ: , .

4. Система двух случайных величин характеризуется математическими ожиданиями , , дисперсиями , и корреляционным моментом . Определить математическое ожидание и дисперсию случайной величины .

Ответ: , .

5. Случайные величины и имеют математические ожидания , и дисперсии и . Найти математическое ожидание случайной величины .

Ответ: .

6. Имеются две случайные величины и , связанные соотношением . Найти корреляционный момент, если известно, что математическое ожидание и дисперсия .

Ответ: .