2. Закон распределения функции двух случайных величин.

Пусть случайная величина является функцией двух случайных величин, образующих систему , т. е. . Наша задача состоит в том, чтобы по известному распределению системы найти распределение случайной величины .

Пусть - плотность распределения системы случаных величин . Введем в рассмотрение новую величину , равную и рассмотрим систему уравнений

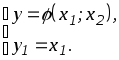
Будем полагать, что эта система однозначно разрешима относительно ,

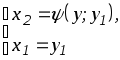
и удовлетворяет условиям дифференцируемости. В результате (опуская выкладки) получим плотность распределения случайной величины :

.

Заметим, что рассуждения не изменяются, если введенную новую величину положить равной .

3. Математическое ожидание функции случайных величин.

На практике часто встречаются случаи, когда нет особой надобности полностью определять закон распределения функции случайных величин, а достаточно только указать его числовые характеристики. Таким образом, возникает задача определения числовых характеристик функций случайных величин, помимо законов распределения этих функций.

Пусть случайная величина является функцией случайного аргумента с заданным законом распределения

Требуется, не находя закона распределения величины , определить ее математическое ожидание

.

Вначале пусть - дискретная случайная величина, имеющая ряд распределения:

			...
			...

Cоставим таблицу значений величины и вероятностей этих значений:

			...
			...

Эта таблица не является рядом распределения случайной величины , т. к. в общем случае некоторые из значений могут совпадать между собой и значения в верхней строке не обязательно идут в возрастающем порядке. Однако математическое ожидание случайной величины можно определить по формуле

, (6.4)

т. к. величина, определяемая формулой (6.4), не может измениться от того, что под знаком суммы некоторые члены будут заранее объединены, а порядок членов изменен. В формуле (6.4) не содержится в явном виде закон распределения самой функции , а содержится только закон распределения аргумента . Таким образом, для определения математического ожидания функции вовсе не требуется знать закон распределения функции , а достаточно знать закон распределения аргумента .

Если в формуле (6.4) сумму заменить интегралом, а вероятность - элементом вероятности, то получим аналогичную формулу для непрерывной случайной величины:

,

где есть плотность распределения случайной величины .

Рассмотрим случаи, когда для нахождения математического ожидания функции случайных аргументов не требуется знать даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики. Сфлрмулируем эти случаи в виде следующих теорем.

Теорема 6.1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин.

.

Теорема 6.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:

.

Следствие 6.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.

Следствие 6.2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.