§ 3. Комплексное представление бигармонической функции.

Из результатов предыдущего параграфа можно сделать вывод о том, что решение любой граничной задачи плоской теории упругости, то есть задачи об отыскании такого решения системы дифференциальных уравнений (1.1)-(1.3), которое удовлетворяет заданным граничным условиям в области, занятой телом, сводится к отысканию лишь одной бигармонической функции напряжений . Можно еще более упростить решение задачи плоской теории упругости, сведя их к определению двух аналитических функций в области, занятой упругим телом. Покажем это.

Пусть – некоторая бигармоническая функция. С этой функцией связываем гармоническую функцию

.

При помощи функции построим пару сопряженных гармонических функцийи, которые определяют аналитическую функциюв области, занятой упругим телом. Пусть–функция, сопряженная, положим

.

Рассмотрим функцию . Подействуем на нее оператором Лапласа, получим

,

так как . Следовательно, функцияявляется гармонической в области. Таким образом, произвольная бигармоническая функцияможет быть представлена в виде

,

где и– сопряженные гармонические функции, а– гармоническая функция.

Введем в рассмотрение аналитическую функцию

,

тогда предыдущее выражение для бигармонической функции можно записать в таком виде

, (3.1)

где – действительная часть комплексного числа,,,. Полученная формула определяет искомое представление бигармонической функциичерез две аналитические функциии.

Для определения напряжений и перемещений в упругом теле важно знать не столько функцию напряжений, сколько ее производные по переменным и. Вычислим первые и вторые производные функции напряжений (3.1). Имеем

.

Аналогично

.

Воспользуемся тем, что для любого комплексного числа верно равенство:

.

Тогда можно написать

,

.

Удобно в приложениях рассматривать комплексную комбинацию первых производных функции напряжения

. (3.2)

Вычислим теперь вторые производные от функции . Имеем

,

,

. (3.3)

Из полученных выражений для вторых производных функции напряжения вытекает, что

. (3.4)

§ 4. Комплексные представления напряжений и перемещений (формулы Колосова-Мусхелишвили).

Обратимся к формулам (2.6) для перемещений точек упругого тела при плоской деформации. Умножим вторую формулу на и сложим с первой формулой, получим

.

Для преобразования правой части равенства воспользуемся формулой (3.2) для и тем, что. Тогда придем к следующему комплексному представлению перемещений

, (4.1)

где – аналитическая функция в области, занятой телом.

Рассмотрим теперь линейные комбинации напряжений и. Согласно формулам (2.1), (3.3), (3.4), используя функциии, получаем

,

.

Таким образом,

, (4.2)

. (4.3)

В этих формулах

, ,. (4.4)

Формулы (4.1)-(4.3) называются формулами Колосова-Мусхелишвили. Из этих формул вытекает, что для определения напряжений и перемещений в упругом теле достаточно найти две аналитические функции ив области, занятой телом. Если же требуется определить только напряжения в теле, то для этого достаточно найти две аналитические функциии.

Поясним механический смысл функции

.

П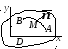усть– область, занятая упругим телом, аи– две различные точки этой области. Соединим эти точки какой-либо гладкой дугой. Установим на ней положительное направление от точкик точке. Так как дуга гладкая, то с каждой ее точкой можно связать единичный вектор, нормальный к касательной (единичный нормальный вектор). Считаем, что векторнаправлен вправо, если двигаться по дуге в положительном направлении.

Отбросим часть тела, расположенную справа от дуги , и заменим действие отброшенной части тела на оставшуюся нагрузками, распределенными вдоль дуги. Обозначим через– вектор напряжения в точкедуги по сечению с внешней нормалью. Тогда, очевидно, интеграл

будет главным вектором распределенной по дуге нагрузки. Пустьипроекции векторана осиисоответственно. Тогда, как показано в монографии [],

. (4.5)

В правой части равенства стоит разность значений функции в точкахи.