
- •4 Лінійні та евклідові простори
- •4.1 Лінійні простори
- •4.2 Дійсний евклідовий простір
- •4.3 Ортонормований базис в евклідовому просторі
- •4.4 Ортогональне доповнення підпростору евклідового простору. Ізоморфізм евклідових просторів
- •4.5 Комплексний евклідовий (унітарний) простір
- •Приклади розв’язування задач
- •Тест для самоконтролю
- •Завдання для самостійного розв’язування
Тест для самоконтролю
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А. |
Б.
|
В.
|
Г.
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А. 5 |
Б. 8 |
В. 9 |
Г. 7 |
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А. 3 |
Б. 1 |
В. 2 |
Г.
|
| |||
|
А. |
Б.
|
В.
|
Г. |
| |||
|
А.
будь-який вектор
|
Б.
лише нульовий вектор
|
В.
будь-який ненульовий вектор
|
Г.
вектор
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
| |||
|
А.
|
Б.
|
В.
|
Г.
|
Відповіді: 1. 2. 3. 4. 5. 6. 7. 8. 9. 11. 12. 13. 14. 15.
Завдання для самостійного розв’язування
З'ясуйте, чи є дійсними лінійними просторами наступні множини зі звичайними операціями додавання та множення:
1.
![]() – множина всіх натуральних чисел;
– множина всіх натуральних чисел;
2.
![]() – множина всіх цілих чисел;
– множина всіх цілих чисел;
3.
![]() – множина всіх раціональних чисел;
– множина всіх раціональних чисел;
4.
![]() – множина всіх дійсних чисел;
– множина всіх дійсних чисел;
5.
![]() – множина всіх комплексних чисел;
– множина всіх комплексних чисел;
6.
![]() – множина всіх додатних дійсних чисел.
– множина всіх додатних дійсних чисел.
З'ясуйте, чи є дійсними лінійними просторами наступні множини вільних векторів зі звичайними операціями додавання та множення на число векторів (за правилами векторної алгебри):
1.
![]() – множина всіх векторів, паралельних
заданій прямій;
– множина всіх векторів, паралельних
заданій прямій;
2.
![]() – множина всіх векторів, паралельних
заданій площині;
– множина всіх векторів, паралельних
заданій площині;
3.
![]() – множина всіх векторів простору;
– множина всіх векторів простору;
4. множина всіх векторів, не паралельних даній прямій.
З'ясуйте, чи є дійсними лінійними просторами над полем
 множини матриць зі звичайними операціями
додавання та множення на елемент поля
множини матриць зі звичайними операціями
додавання та множення на елемент поля (у випадку позитивної відповіді вкажіть
який-небудь базис):
(у випадку позитивної відповіді вкажіть
який-небудь базис):
1.
![]() – множина всіх прямокутних
– множина всіх прямокутних![]() -
матриць з дійсними елементами;
-
матриць з дійсними елементами;
2.
![]() – множина всіх
– множина всіх![]() -
матриць з дійсними елементами;
-
матриць з дійсними елементами;
3.
![]() – множина всіх матриць другого порядку
з комплексними елементами;
– множина всіх матриць другого порядку
з комплексними елементами;
4.
![]() ;
5.
;
5.![]() ;
6.
;
6.![]() .
.
З'ясуйте, чи є дійсними лінійними просторами наступні множини:
1. множина
![]() всіх многочленів степеня, не вище
всіх многочленів степеня, не вище![]() ;
;
2. множина
всіх многочленів степеня
![]() ;
;
3. множина всіх многочленів, що задовольняють умовам:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
4. множина
![]() всіх неперервних на
всіх неперервних на![]() функцій;
функцій;
5. множина
всіх розривних на
![]() функцій;
функцій;
6. множина
всіх функцій, інтегрованих на
![]() функцій.
функцій.
Доведіть, що система векторів, що вміщує нульовий вектор, лінійно залежна.
Доведіть, що система векторів, два вектори якої розрізняються лише скалярним множником, лінійно залежна.
Доведіть, що довільна підсистема лінійно залежної системи, лінійно залежна.
Чи вірно, що якщо
 – лінійно залежні вектори, то ця
властивість притаманна векторам
– лінійно залежні вектори, то ця
властивість притаманна векторам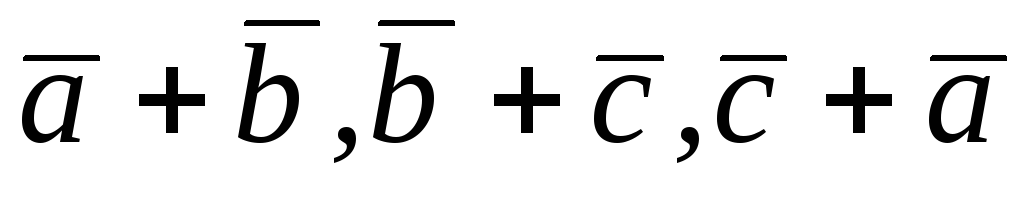 ?
?Якій умові повинно відповідати число
 ,
щоб вектори
,
щоб вектори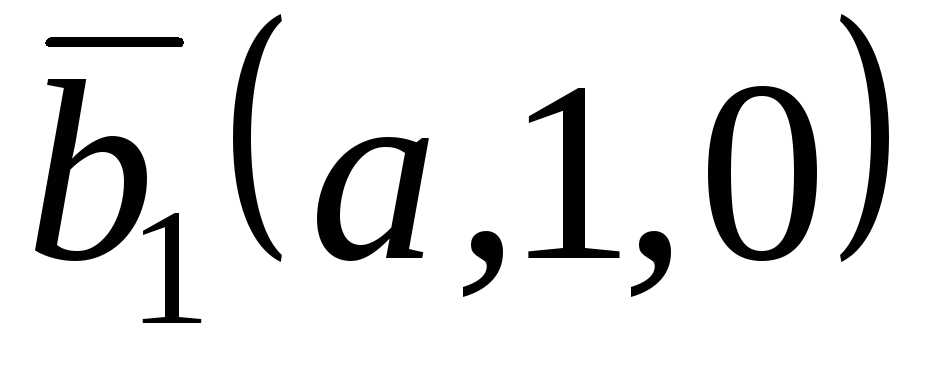 ,
, ,
, були лінійно залежні?
були лінійно залежні?Якій умові повинні відповідати числа
 ,
щоб вектори
,
щоб вектори ,
, ,
, простору
простору були лінійно залежні?
були лінійно залежні?Доведіть, що системи векторів дійсного простору лінійно залежні, знайдіть їх нетривіальну нульову лінійну комбінацію, якщо:
1.
![]() ,
,![]() ,
,![]() ;
;
2.
![]() ,
,![]() ,
,![]() ;
;
3.
![]() ,
,![]() ,
,![]() ;
;
4.
![]() ,
,![]() ,
,![]() ;
;
5.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
З’ясуйте, чи є дані вектори (функції) лінійно залежними. У випадку позитивної відповіді знайдіть їх нетривіальну нульову лінійну комбінацію:
1.
 ;
;4.
 ;
;7.
 ;
;2.
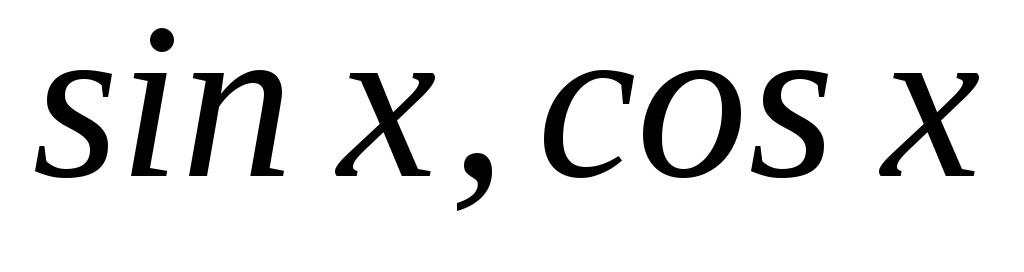 ;
;5.
 ;
;8.
 ;
;3.
 ;
;6.
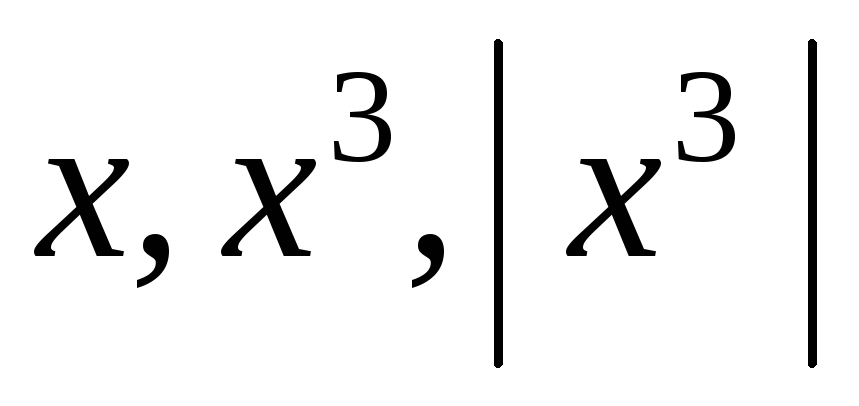 ;
;9.
 .
.В базисі
 дійсного лінійного простору
дійсного лінійного простору знайдіть координати вектора
знайдіть координати вектора .
.В базисі
 ,
, ,
, дійсного лінійного простору
дійсного лінійного простору знайдіть координати векторів
знайдіть координати векторів ,
, .
.Перевірте, що в просторі
 многочленів над
многочленів над степеня не вище 4 дана система утворює
базис та знайдіть координати вектора
степеня не вище 4 дана система утворює
базис та знайдіть координати вектора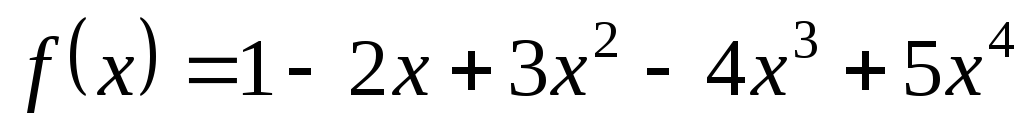 в кожному з цих базисів:
в кожному з цих базисів:
1.
![]() ; 2.
; 2.![]() ;
;
3.
![]() .
.
Перевірте, чи утворює кожна з наступних систем рядків базис у просторі
 .
У випадку позитивної відповіді знайдіть
координати рядка
.
У випадку позитивної відповіді знайдіть
координати рядка в кожному з базисів:
в кожному з базисів:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
Запишіть матрицю переходу від базису
 до базису
до базису та знайдіть координати векторів
та знайдіть координати векторів та
та в цих базисах:
в цих базисах:
1.
![]() ;
;![]() ;
;
2.
![]() ;
;![]()
![]()
![]() ;
;
3.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
4.
![]() ;
;![]() ;
;
5.
![]() ;
;![]()
![]() .
.
Матриця
 є матрицею переходу від першого базису
є матрицею переходу від першого базису у
у -
вимірному лінійному просторі до другого
базису
-
вимірному лінійному просторі до другого
базису ,
а матриця
,
а матриця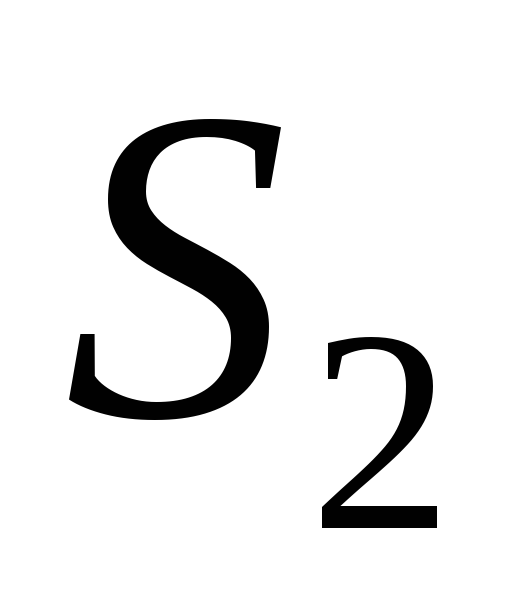 – матриця переходу від другого базису
до третього
– матриця переходу від другого базису
до третього .
Знайдіть матрицю переходу: 1. від першого
базису до третього; 2. від другого базису
до першого.
.
Знайдіть матрицю переходу: 1. від першого
базису до третього; 2. від другого базису
до першого.З’ясуйте, чи є наступні системи векторів лінійно залежними:
1.
![]() ; 2.
; 2.![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() .
.
Знайдіть всі значення
 ,
при яких вектор
,
при яких вектор лінійно виражається через
лінійно виражається через :
:
1.
![]() ;
;
2.
![]() .
.
Знайдіть ранг та який-небудь базис системи векторів (відповідного лінійного простору):
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]()
![]() ;
;
5.
![]() ,
,![]() ,
,![]() ;
;
6.
![]() .
.
Доведіть, що вектори
 утворюють базис у комплексному
утворюють базис у комплексному -
вимірному арифметичному просторі та
знайдіть координати вектора
-
вимірному арифметичному просторі та
знайдіть координати вектора у цьому базисі:
у цьому базисі:
1.
![]() ;
;
2.
![]()
![]() .
.
Доведіть, що кожна з двох систем векторів
 та
та є базисом у комплексному
є базисом у комплексному -
вимірному арифметичному просторі та
знайдіть матрицю переходу від першого
базису до другого, якщо:
-
вимірному арифметичному просторі та
знайдіть матрицю переходу від першого
базису до другого, якщо:
1.
![]() ;
;
2.
![]()
![]() .
.
Доповніть до базису відповідного простору систему векторів:
1.
![]() ; 2.
; 2.![]() ;
;
3.
![]() ; 4.
; 4.![]() ;
;
5.
![]() ;
;
6.
![]() .
.
Укажіть, які з даних множин є підпросторами лінійній дійсних просторів. Знайдіть один з базисів та розмірність кожного з підпросторів:
1. множина всіх вільних векторів, ортогональних даній площині;
2. множина всіх вільних векторів, паралельних даній площині;
3. множина всіх вільних векторів, ортогональних даній прямій;
4. множина
всіх векторів
![]() -
вимірного векторного простору, координати
яких – цілі числа;
-
вимірного векторного простору, координати
яких – цілі числа;
5.
![]() ;
6.
;
6.![]() ;
;
7. множина
дійсних симетричних матриць порядку
![]() ;
;
8. множина
всіх дійсних кососиметричний матриць
порядку
![]() .
.
Доведіть, що наступні системи векторів утворюють лінійні підпростори, знайдіть їх базис та розмірність:
1. всі
![]() -
вимірні вектори, у яких перша та остання
координати рівні між собою;
-
вимірні вектори, у яких перша та остання
координати рівні між собою;
2. всі
![]() -
вимірні вектори, у яких координати з
парними номерами дорівнюють нулю;
-
вимірні вектори, у яких координати з
парними номерами дорівнюють нулю;
3. всі
![]() -
вимірні вектори, у яких координати з
парними номерами рівні між собою.
-
вимірні вектори, у яких координати з
парними номерами рівні між собою.
Знайдіть базис та розмірність лінійної оболонки наступних систем векторів (відповідного лінійного простору):
1.
![]() ;
;
2.
![]()
![]() ;
;
3.
![]() ;
;
4.
![]() .
.
Визначте розмірність та базис суми та перетину підпросторів
 та
та ,
якщо:
,
якщо:
1.
![]() ;
;
2.
![]() ;
;
3.![]()
![]() ;
;
4.
![]()
![]() ;
;
5.
![]() ,
,![]()
![]()
![]() .
.
Визначте розмірність та базис суми та перетину лінійних підпросторів
 та
та комплексного
комплексного -
вимірного арифметичного простору,
якщо:
-
вимірного арифметичного простору,
якщо:
1.
![]()
![]() ;
;
2.
![]() ,
,
![]()
![]() .
.
Нехай
 – довільні вектори
– довільні вектори -
вимірного евклідового простору. Чи
можна визначити їх скалярний добуток
формулою
-
вимірного евклідового простору. Чи
можна визначити їх скалярний добуток
формулою ?
?Нехай
 – довільні вектори двовимірного
евклідового простору. Чи можна визначити
їх скалярний добуток формулою
– довільні вектори двовимірного
евклідового простору. Чи можна визначити
їх скалярний добуток формулою ?
?Нехай
 – довільні вектори евклідового простору
– довільні вектори евклідового простору .
Визначте, чи можуть наступні функції
задавати скалярний добуток у цьому
просторі. Якщо ні, то укажіть, які
властивості не виконуються.
.
Визначте, чи можуть наступні функції
задавати скалярний добуток у цьому
просторі. Якщо ні, то укажіть, які
властивості не виконуються.
1.
![]() ; 2.
; 2.![]() ;
;
3.
![]() ; 4.
; 4.![]() ,
а)
,
а)![]() ,
б)
,
б)![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() .
.
Нехай
 – довільні вектори унітарного простору
– довільні вектори унітарного простору .
Визначте, чи можуть наступні функції
задавати скалярний добуток у цьому
просторі. Якщо ні, то укажіть, які
властивості не виконуються.
.
Визначте, чи можуть наступні функції
задавати скалярний добуток у цьому
просторі. Якщо ні, то укажіть, які
властивості не виконуються.
1.
![]() ; 2.
; 2.![]() ,
,![]() ;
;
3.
![]() ; 4.
; 4.![]() ;
;
5.
![]() ; 6.
; 6.![]() ;
;
7.
![]() ;
;
8.
![]() .
.
Доведіть, що зі властивостей скалярного добутку випливають наступні властивості:
1.
![]()
![]() евклідового або унітарного простору;
евклідового або унітарного простору;
2.
![]()
![]() евклідового простору,
евклідового простору,![]() ;
;
3.
![]()
![]() унітарного простору,
унітарного простору,![]() ;
;
4.
![]()
![]() евклідового або унітарного простору;
евклідового або унітарного простору;
5.
![]()
![]() евклідового або унітарного простору;
евклідового або унітарного простору;
Нехай
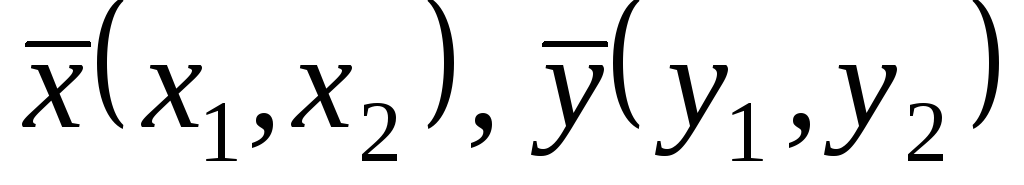 – довільні вектори арифметичного
простору
– довільні вектори арифметичного
простору .
Доведіть, що скалярний добуток у ньому
можна визначити так:
.
Доведіть, що скалярний добуток у ньому
можна визначити так:
1.
![]() ;
;
2.
![]() .
.
Доведіть, що якщо в евклідовому просторі вектор ортогональний векторам
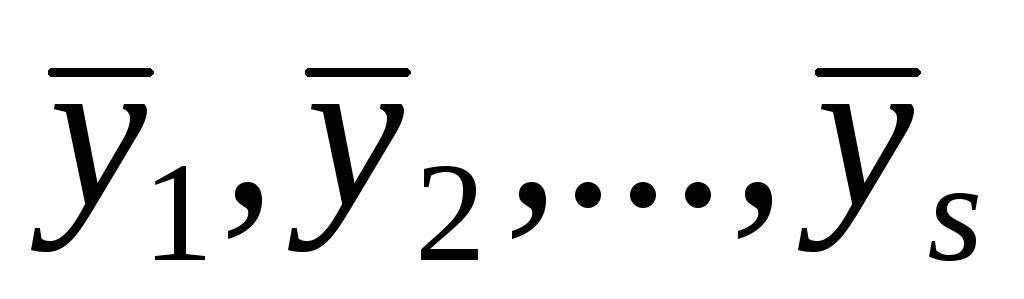 ,
то він ортогональний і довільній їх
лінійній комбінації
,
то він ортогональний і довільній їх
лінійній комбінації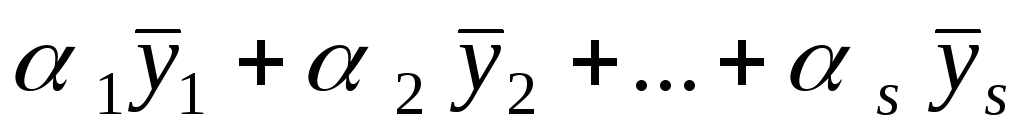 ,
, .
.В лінійному просторі дійсних квадратних матриць порядку
 задано функцію
задано функцію .
Визначте, чи притаманні функції всі
властивості операції евклідового
скалярного добутку, якщо:
.
Визначте, чи притаманні функції всі
властивості операції евклідового
скалярного добутку, якщо:
1.
![]() ; 2.
; 2.![]() ; 3.
; 3.![]() ;
;
4.
![]() .
.
Знайдіть скалярний добуток векторів
 і
і в ортонормованому базисі:
в ортонормованому базисі:
1.
![]() ; 2.
; 2.![]() .
.
Визначте кут між векторами
 і
і в ортонормованому базисі:
в ортонормованому базисі:
1.
![]() ; 2.
; 2.![]() ;
;
3.
![]() .
.
Нехай
 .
Знайдіть довжини цих векторів та
скалярні добутки:
.
Знайдіть довжини цих векторів та
скалярні добутки: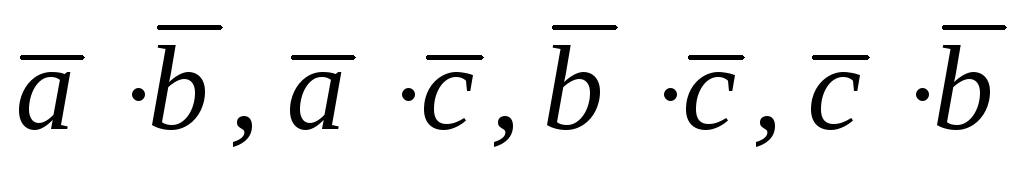 .
.Нормуйте вектор
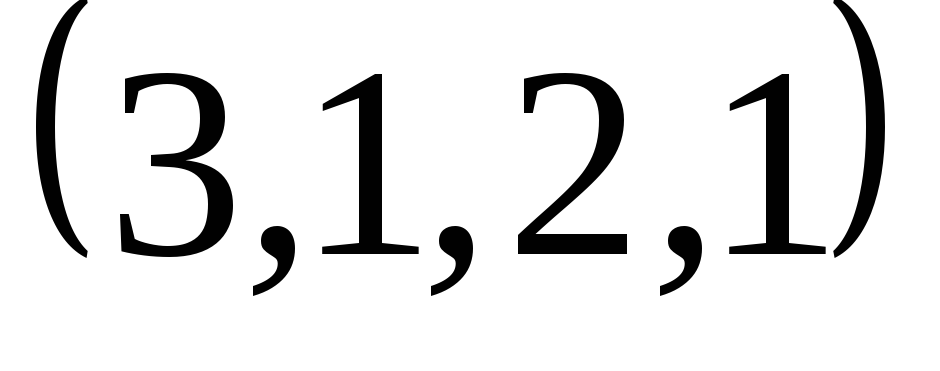 .
.Чи можна задати скалярний добуток формулою
 .
У випадку позитивної відповіді знайдіть
довжини векторів
.
У випадку позитивної відповіді знайдіть
довжини векторів та
та
 ,
якщо,
,
якщо,
 ,
, .
.Чи можна задати скалярний добуток формулою
 .
У випадку позитивної відповіді знайдіть
довжини векторів
.
У випадку позитивної відповіді знайдіть
довжини векторів та
та
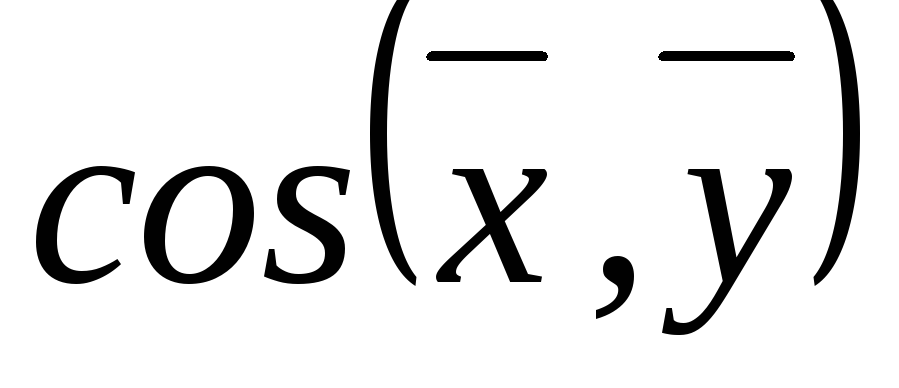 ,
якщо ,
,
якщо ,
 ,
, .
.Визначте косинуси кутів між прямою
 та осями координат
та осями координат -
вимірного евклідового простору.
-
вимірного евклідового простору.Визначте косинуси внутрішніх кутів трикутника АВС, заданого координатами вершин:
 .
.Знайдіть довжини діагоналей n-вимірного куба зі стороною
 .
.Знайдіть число діагоналей n-вимірного куба, ортогональних до даної діагоналі.
У дійсному або комплексному арифметичному просторі скалярний добуток задано як функцію компонент
 та
та векторів
векторів та
та .
Обчисліть матриці Грама стандартного
базису і базису, складеного з даних
векторів
.
Обчисліть матриці Грама стандартного
базису і базису, складеного з даних
векторів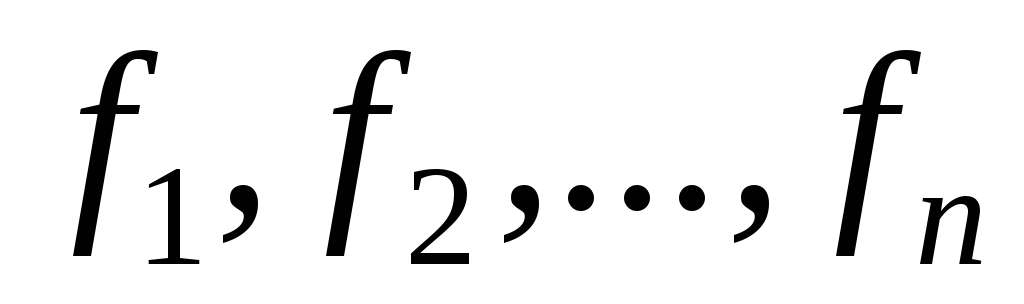 .
Знайдіть вираз скалярного добутку
векторів
.
Знайдіть вираз скалярного добутку
векторів та
та через їх компоненти в базисі
через їх компоненти в базисі .
.
1.
![]() ,
,![]() ;
;
2.
![]() ;
;![]() ;
;
3.
![]() ,
,
![]() ;
;
4.
![]() ,
,
![]() .
.
В евклідовому просторі многочленів степеня, не вище
 ,
зі скалярним добутком
,
зі скалярним добутком обчисліть матрицю Грама базису
обчисліть матрицю Грама базису та випишіть вираз скалярного добутку
та випишіть вираз скалярного добутку через координати векторів
через координати векторів у цьому базисі, якщо: 1.
у цьому базисі, якщо: 1. ;
2.
;
2.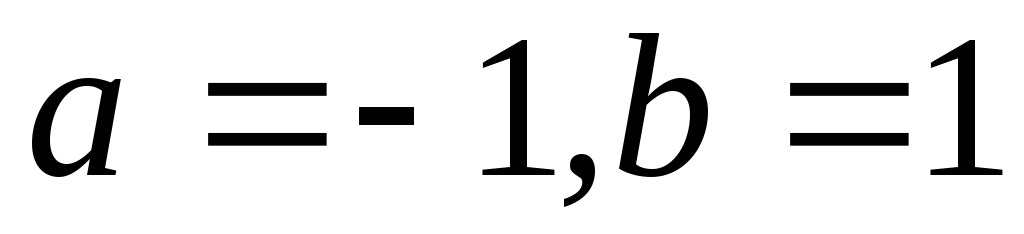 .
.Знайдіть нормований вектор, ортогональний до векторів
 ,
, ,
,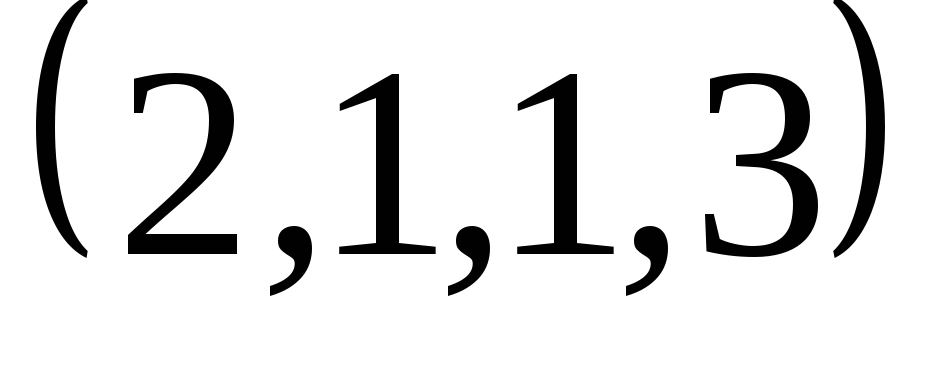 .
.Побудуйте ортонормований базис простору, узявши за два вектори цього базису вектори
 і
і .
.Переконайтеся, що вектори
 ортогональні та доповніть систему
ортогональні та доповніть систему до ортогонального базису, якщо:
до ортогонального базису, якщо:
1.
![]() ; 2.
; 2.![]() ;
;
3.
![]() .
.
Використовуючи процес ортогоналізації, знайдіть ортогональний базис простору (евклідового або унітарного), породженого векторами:
1.
![]() ,
,![]() ,
,![]() ;
;
2.
![]() ,
,![]() ,
,![]() ;
;
3.
![]() ,
,![]() ,
,![]() ;
;
4.
![]() ;
;
5.
![]() .
.
Виходячи зі системи векторів
 арифметичного простору з заданим
скалярним добутком, за допомогою процесу
ортогоналізації побудуйте ортонормований
базис
арифметичного простору з заданим
скалярним добутком, за допомогою процесу
ортогоналізації побудуйте ортонормований
базис ,
якщо:
,
якщо:
1.
![]() ,
скалярний добуток:
,
скалярний добуток:
а)
![]() ;
;
б)
![]() ;
;
2.
![]() ,
скалярний добуток
,
скалярний добуток
![]() .
.
Нехай
 – арифметичний простір, у якому скалярний
добуток визначений формулою:
– арифметичний простір, у якому скалярний
добуток визначений формулою:
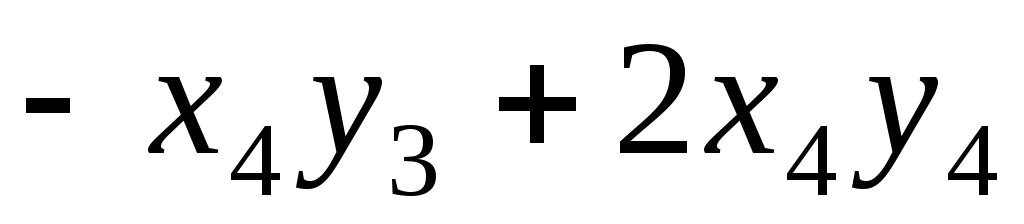 ,
де
,
де – довільні вектори з
– довільні вектори з .
Застосовуючи процес ортогоналізації,
знайдіть ортонормований базис простору
.
Застосовуючи процес ортогоналізації,
знайдіть ортонормований базис простору ,
узявши за вихідний базис:
,
узявши за вихідний базис:
1.
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
2.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Застосовуючи процес ортогоналізації, знайдіть ортонормований базис простору:
1.
![]() многочленів над
многочленів над![]() не вище другого степеня, узявши за
вихідний базис
не вище другого степеня, узявши за
вихідний базис![]() ,
якщо скалярний добуток задано формулою:
,
якщо скалярний добуток задано формулою:
а)
![]() ; б)
; б)![]() ,
де
,
де![]() ;
;
2.
![]() ,
узявши за вихідний базис
,
узявши за вихідний базис![]() ,
якщо скалярний добуток задано формулою
,
якщо скалярний добуток задано формулою![]() ;
;
3.
![]() ,
узявши за вихідний базис
,
узявши за вихідний базис![]() ,
якщо скалярний добуток задано формулою
,
якщо скалярний добуток задано формулою![]() .
.
Знайдіть ортогональний базис ортогонального доповнення
 ,
якщо
,
якщо =
= і:
і:
1.
![]() ,
,![]() ,
,![]() ;
;
2.
![]() ,
,![]() ,
,![]() .
.
Дано матрицю
 .
.
Побудуйте ще два її рядки, ортогональні між собою та з першими трьома рядками.
Знайдіть ортогональну й нормовану фундаментальну систему розв’язків для системи рівнянь
![]()
Розкладіть вектор
 на суму двох векторів, один з яких лежить
у просторі, натягнутому на вектори
на суму двох векторів, один з яких лежить
у просторі, натягнутому на вектори ,
а другий ортогональний до цього простору
(ортогональна проекція і ортогональна
складова вектора
,
а другий ортогональний до цього простору
(ортогональна проекція і ортогональна
складова вектора ),
якщо:
),
якщо:
1.
![]() ;
;
2.
![]() .
.
Знайдіть ортогональну проекцію
 і ортогональну складову
і ортогональну складову вектора
вектора на лінійний простір
на лінійний простір ,
,
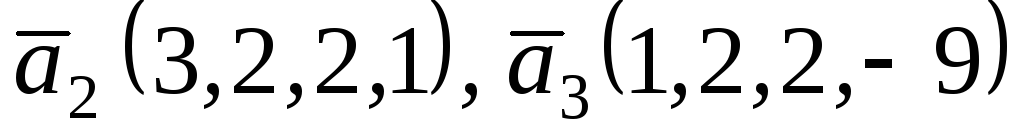 .
.Знайдіть найменший кут між векторами простору Р, натягнутого на вектори
 ,
і вектором
,
і вектором ,
якщо:
,
якщо:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() .
.






 .
.