
5 Оператори
В теорії лінійних просторів важливу роль відіграють лінійні оператори, які ще називають лінійними «перетвореннями» простору.
У
векторному просторі
![]() задано оператор, якщо вказано правило
(закон), за яким кожному вектору
задано оператор, якщо вказано правило
(закон), за яким кожному вектору![]() ставиться у відповідність деякий вектор
ставиться у відповідність деякий вектор![]() .
Вектор
.
Вектор![]() називають образом вектора
називають образом вектора![]() ,
а
,
а![]() – прообразом вектора
– прообразом вектора![]() .
.
Отже,
оператор у векторному просторі
![]() – це функція, множиною визначення і
множиною значень якої є простір
– це функція, множиною визначення і
множиною значень якої є простір![]() .
.
Оператори
позначають буквами
![]() .
.
Образ
вектора
![]() при дії оператора
при дії оператора![]() позначають символом
позначають символом![]() .
.
Оператори
в просторі
![]() називають ще операторами простору
називають ще операторами простору![]() ,
перетвореннями простору
,
перетвореннями простору![]() ,
відображенням простору
,
відображенням простору![]() в себе.
в себе.
Оператор
![]() у векторному просторі
у векторному просторі![]() називаютьлінійним,
якщо він задовольняє наступним умовам:
називаютьлінійним,
якщо він задовольняє наступним умовам:
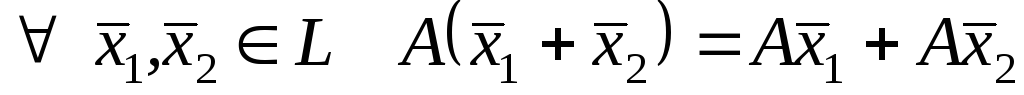 ;
;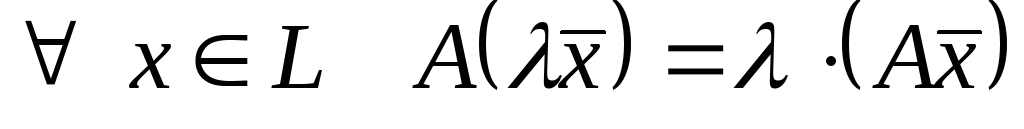 .
.
Із означення лінійного оператора випливають наступні властивості:
Будь-який лінійний оператор
 в просторі
в просторі залишає нерухомим нульовий вектор
залишає нерухомим нульовий вектор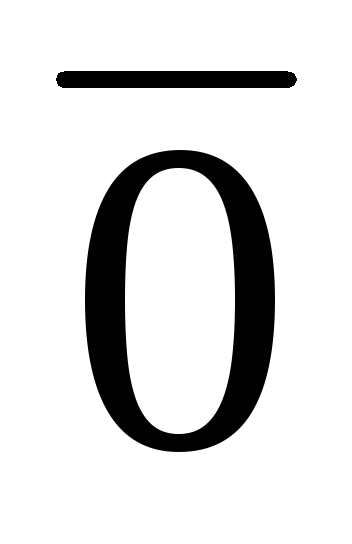 цього простору, тобто
цього простору, тобто .
.Будь-який лінійний оператор
 в просторі
в просторі протилежному вектору
протилежному вектору довільного вектора
довільного вектора ставить у відповідність вектор,
протилежний образу вектора
ставить у відповідність вектор,
протилежний образу вектора .
.Лінійний оператор
 в просторі
в просторі будь-якій лінійній комбінації довільно
вибраних векторів
будь-якій лінійній комбінації довільно
вибраних векторів простору
простору ставить у відповідність лінійну
комбінацію (з тими ж коефіцієнтами)
образів цих векторів.
ставить у відповідність лінійну
комбінацію (з тими ж коефіцієнтами)
образів цих векторів.
З’ясуємо,
якими елементами можна задати лінійний
оператор в просторі
![]() .
.
Задати
лінійний оператор
![]() в просторі
в просторі![]() – це означає задати образи всіх векторів
кожного базису цього простору.
– це означає задати образи всіх векторів
кожного базису цього простору.
Якщо
відомі образи всіх векторів одного з
базисів простору
![]() при дії оператора
при дії оператора![]() ,
то можна знайти образи всіх векторів
простору при дії цього оператора.
,
то можна знайти образи всіх векторів
простору при дії цього оператора.
Теорема
1.
Будь-який оператор
![]() в просторі
в просторі![]() однозначно визначається заданням
образів
однозначно визначається заданням
образів![]() всіх векторів будь-якого фіксованого
базису
всіх векторів будь-якого фіксованого
базису![]() цього простору.
цього простору.
Доведення:
Нехай
![]() – один з базисів простору
– один з базисів простору![]() ,
тоді
,
тоді![]() можна представити
можна представити![]() ,
де
,
де![]() .
.
Подіємо
на вектор
![]() лінійним оператором
лінійним оператором![]() :
:
![]() .
.
Нехай
вектори
![]() – образи векторів базису при дії
лінійного оператора
– образи векторів базису при дії
лінійного оператора![]() ,
тоді
,
тоді
![]() .
.
Отже,
образ вектора
![]() визначається і до того ж однозначно.
визначається і до того ж однозначно.
Теорема
2.
Якою б не була впорядкована система з
![]() векторів
векторів![]() простору
простору![]() існує, і до того ж тільки один, лінійний
оператор
існує, і до того ж тільки один, лінійний
оператор![]() простору
простору![]() такий, що вектори цієї системи будуть
образами векторів базису
такий, що вектори цієї системи будуть
образами векторів базису![]() при дії цього оператора.
при дії цього оператора.
Доведення:
Довільний вектор
![]() в базисі
в базисі![]() має вигляд
має вигляд![]() .
Вектору
.
Вектору![]() поставимо у відповідність вектор
поставимо у відповідність вектор![]() .
Оскільки вектор
.
Оскільки вектор![]() виражається через вектори базису
однозначно, то йому у відповідність
ставиться тільки один вектор
виражається через вектори базису
однозначно, то йому у відповідність
ставиться тільки один вектор![]() .
.
Отже,
задана таким чином відповідність є
оператором в просторі
![]() ,
позначимо його через
,
позначимо його через![]() .
.
Тоді
![]() .
Оператор
.
Оператор![]() – лінійний.
– лінійний.
Дійсно, нехай
![]() ,
,
![]() ,
,
тоді
![]() .
.
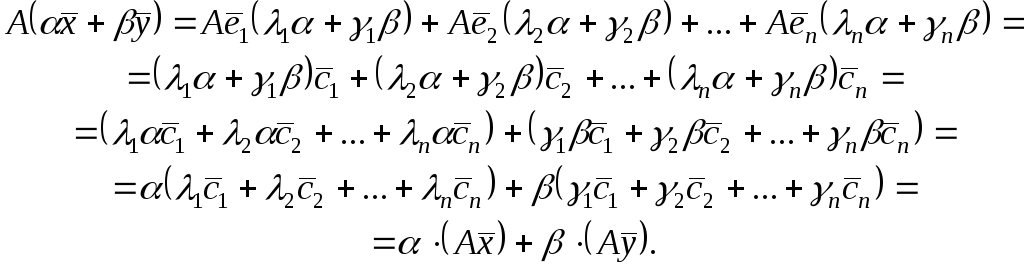
Оператор
![]() відображає вектори
відображає вектори![]() у вектори
у вектори![]() .
Дійсно, оскільки
.
Дійсно, оскільки![]() а
координата вектора
а
координата вектора![]() в базисі
в базисі![]() дорівнює 1, а всі інші його координати
дорівнюють нулю, то
дорівнює 1, а всі інші його координати
дорівнюють нулю, то![]() .
.
Отже,
заданий оператор
![]() задовольняє вимогам теореми 2, а за
теоремою 1, такий оператор існує тільки
один. Теорему доведено.
задовольняє вимогам теореми 2, а за
теоремою 1, такий оператор існує тільки
один. Теорему доведено.
Нехай
![]() – деякий лінійний оператор в
– деякий лінійний оператор в![]() ,
,![]() – будь-який базис цього простору.
Оператор
– будь-який базис цього простору.
Оператор![]() відображає вектори цього базису в деякі
вектори
відображає вектори цього базису в деякі
вектори![]() кожний з яких одночасно виражається
через вектори базису
кожний з яких одночасно виражається
через вектори базису![]() .
.
Нехай
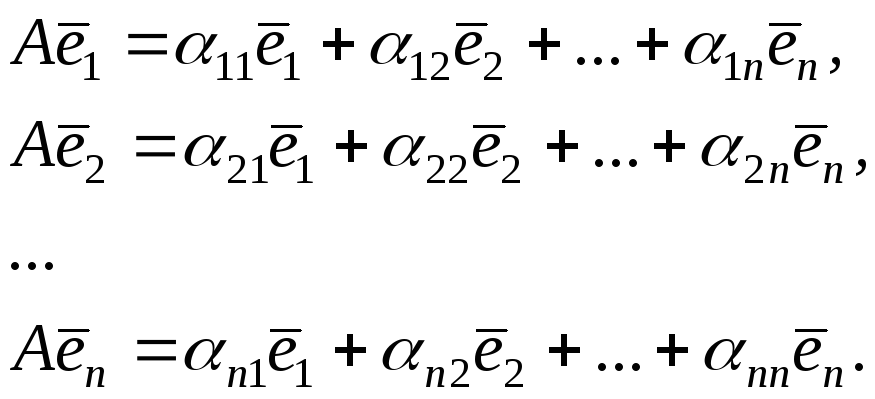
З
коефіцієнтів
![]() складаємо матрицю
складаємо матрицю
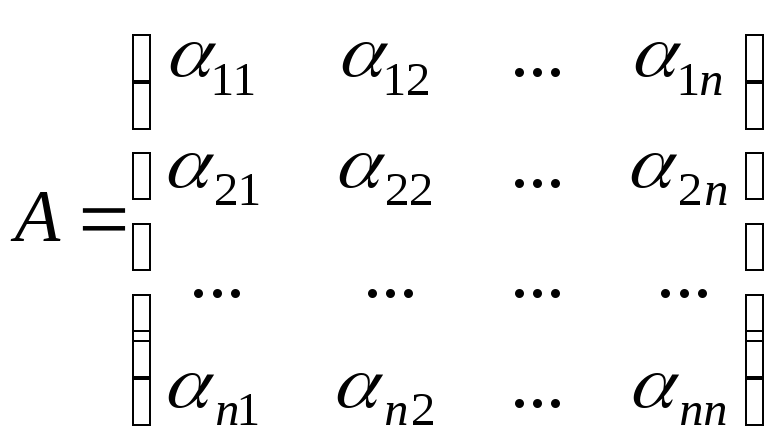 ,
,
рядками
якої є координатні рядки векторів
![]() в базисі
в базисі![]() .
.
Оскільки
координатні рядки векторів
![]() визначаються однозначно, то і матриця
визначаються однозначно, то і матриця![]() визначається оператором
визначається оператором![]() однозначно.
однозначно.
Матрицю
![]() називаютьматрицею
лінійного оператора
називаютьматрицею
лінійного оператора
![]() в базисі
в базисі![]() .
.
Отже в
базисі
![]() лінійний оператор
лінійний оператор![]() задається матрицею
задається матрицею![]() .
.
При
фіксованому базисі
![]() кожному лінійному оператору
кожному лінійному оператору![]() простору
простору![]() відповідає певним чином визначена
матриця
відповідає певним чином визначена
матриця![]() ого
порядку – матриця цього лінійного
оператора.
ого
порядку – матриця цього лінійного
оператора.
І,
навпаки, кожна матриця
![]() ого
порядку
ого
порядку![]() є матрицею деякого лінійного оператора
простору
є матрицею деякого лінійного оператора
простору![]() в базисі
в базисі![]() .
.
Дійсно,
знаючи матрицю
![]() ,
знайдемо вектори:
,
знайдемо вектори:
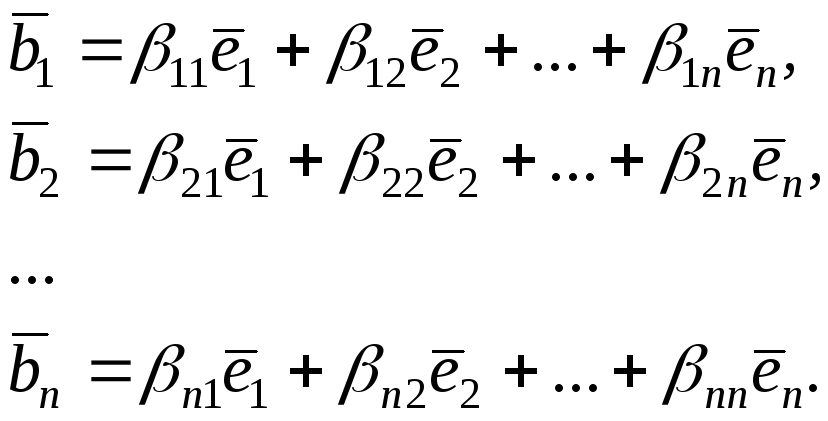
За теоремою 2 визначимо лінійний оператор.
В просторі
![]() ,
який вектори
,
який вектори![]() відображає відповідно у вектори
відображає відповідно у вектори![]() .
Оператор
.
Оператор![]() – єдиний, його матрицею в базисі
– єдиний, його матрицею в базисі![]() є матриця
є матриця![]() .
.
Отже,
якщо в лінійному просторі
![]() над полем
над полем![]() обрано базис
обрано базис![]() і кожному оператору
і кожному оператору![]() простору
простору![]() поставлено у відповідність матрицю
поставлено у відповідність матрицю![]() цього оператора в базисі
цього оператора в базисі![]() ,
то цим буде встановлена взаємно-однозначна
відповідність між всіма лінійними
операторами простору
,
то цим буде встановлена взаємно-однозначна
відповідність між всіма лінійними
операторами простору![]() і всіма матрицями
і всіма матрицями![]() ого
порядку над полем
ого
порядку над полем![]() .
.
З’ясуємо,
як знаючи матрицю лінійного оператора
![]() і координати вектора
і координати вектора![]() в базисі
в базисі![]() ,
знайти координати вектора
,
знайти координати вектора![]() в цьому ж базисі.
в цьому ж базисі.
Нехай
![]() – матриця оператора
– матриця оператора![]() в базисі
в базисі![]() і вектор
і вектор![]() .
Тоді
.
Тоді![]() .
.
Але
![]() .
Тому
.
Тому
![]()
Позначаючи
координатний стовпець вектора
![]() через
через![]() ,
а координатний стовпець вектора
,
а координатний стовпець вектора![]() – символом
– символом![]() ,
одержуємо
,
одержуємо
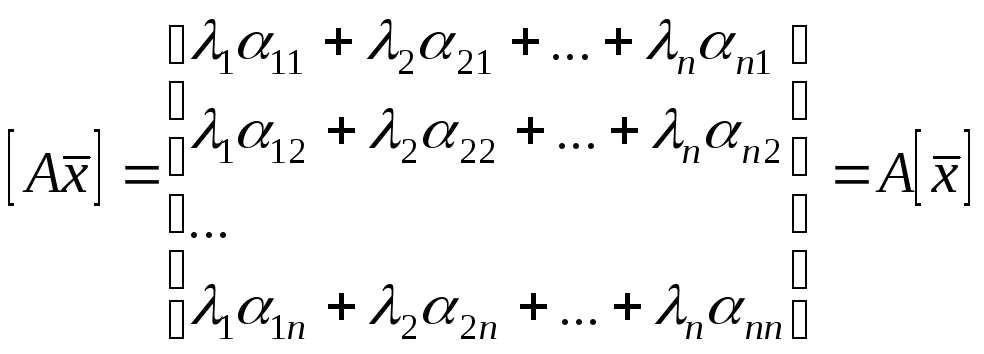 ,
,
тобто
![]() .
.
Отже, справедливе твердження:
Координатний
стовпець вектора
![]() в базисі
в базисі![]() дорівнює добутку матиці лінійного
оператора та координатного стовпця
вектора
дорівнює добутку матиці лінійного
оператора та координатного стовпця
вектора![]() в цьому базисі.
в цьому базисі.
Матриці є тим аналітичним апаратом, за допомогою якого вивчаються лінійні оператори в скінченновимірних просторах.
Кожний
лінійний оператор простору
![]() задається в обраному базисі певною
матрицею. При зміні базису матриця
лінійного оператору також буде
змінюватися. Як же пов’язані матриці,
які задають один і той же оператор, в
різних базисах?
задається в обраному базисі певною
матрицею. При зміні базису матриця
лінійного оператору також буде
змінюватися. Як же пов’язані матриці,
які задають один і той же оператор, в
різних базисах?
Лема:
Нехай
![]() і
і![]() ,
,![]() – матриці над полем
– матриці над полем![]() .
Якщо для будь-якого стовпця
.
Якщо для будь-якого стовпця![]() з елементами з поля
з елементами з поля![]()
![]() ,
то
,
то![]() .
.
Теорема.
Якщо лінійний оператор
![]() простору
простору![]() задається в базисі
задається в базисі![]() матрицею
матрицею![]() ,
то в базисі
,
то в базисі![]() він задається матрицею
він задається матрицею![]() ,
де
,
де![]() – матриця переходу від базису
– матриця переходу від базису![]() до базису
до базису![]() .
.
Доведення:
Нехай
![]() і
і![]() – деякі базиси простору
– деякі базиси простору![]() ,
,![]() – матриця переходу від базису
– матриця переходу від базису![]() до базису
до базису![]() і
і![]() – матриці оператора
– матриці оператора![]() в базисах
в базисах![]() і
і![]() відповідно. Позначимо символами
відповідно. Позначимо символами![]() і
і![]() координатні стовпці довільного вектора
координатні стовпці довільного вектора![]() простору
простору![]() в базисах
в базисах![]() і
і![]() ,
асимволами
,
асимволами
![]() і
і![]() – координатні стовпці вектора
– координатні стовпці вектора![]() в цих базисах.
в цих базисах.
Тоді
![]() ,
,
![]() .
.
Але
![]() ,
,![]() .
.
Одержуємо
![]() .
.
![]() ;
;
![]() .
.
З’ясуємо,
що являє собою матриця переходу
![]() від базису
від базису
![]() до
базису
до
базису
![]() з точки зору теорії лінійних операторів.
з точки зору теорії лінійних операторів.
Існує
тільки один лінійний оператор
![]() ,
який переводить вектори базису
,
який переводить вектори базису![]() у відповідні вектори базису
у відповідні вектори базису![]() такий, що
такий, що
![]()
![]()
Рядками
матриці оператору
![]() в базисі
в базисі![]() є координатні рядки векторів
є координатні рядки векторів![]() в цьому базисі. Але координатні рядки
векторів
в цьому базисі. Але координатні рядки
векторів![]() в базисі
в базисі![]() є рядками і матриці переходу
є рядками і матриці переходу![]() від базису
від базису![]() до базису
до базису![]() .
.
Отже,
матриця переходу
![]() є матрицею оператора
є матрицею оператора![]() ,
який переводить базис
,
який переводить базис![]() в базис
в базис![]() ,
обчислена в базисі
,
обчислена в базисі![]() .
Але матриця переходу
.
Але матриця переходу![]() є матрицею оператора
є матрицею оператора![]() в базисі
в базисі![]() .
.
Дійсно,
матрицею оператора
![]() в базисі
в базисі![]() є матриця
є матриця![]() ;
матрицею переходу від базису
;
матрицею переходу від базису![]() до базису
до базису![]() є також матриця
є також матриця![]() .
Тому матрицею оператора
.
Тому матрицею оператора![]() в базисі
в базисі![]() є матриця
є матриця
![]() .
.
Нехай
![]() і
і![]() – матриці
– матриці![]() ого
порядку над полем
ого
порядку над полем![]() .
.
Означення.
Матриця
![]() називається подібною до матриці
називається подібною до матриці![]() ,
якщо існує така невироджена матриця
,
якщо існує така невироджена матриця![]() ого
порядку
ого
порядку![]() над полем
над полем![]() ,
що
,
що
![]() .
.
Теорема.
На множині
![]() всіх матриць
всіх матриць![]() ого
порядку над полем
ого
порядку над полем![]() подібність матриць є відношенням
еквівалентності.
подібність матриць є відношенням
еквівалентності.
Доведення:
Кожна матриця
![]() подібна собі, оскільки
подібна собі, оскільки![]() (рефлексивність).
(рефлексивність).
Якщо
матриця
![]() подібна матриці
подібна матриці![]() ,
то матриця
,
то матриця![]() подібна матриці
подібна матриці![]() :
:
![]() ,
,
тобто
![]() (симетричність).
(симетричність).
Якщо
матриця
![]() подібна матриці
подібна матриці![]() ,
а матриця
,
а матриця![]() подібна матриці
подібна матриці![]() ,
то матриця
,
то матриця![]() подібна матриці
подібна матриці![]() :
:
![]() .
.
Оскільки
подібність матриць є відношенням
еквівалентності, то множина всіх матриць
![]()
![]() ого
порядку над полем
ого
порядку над полем![]() розбивається на класи подібних матриць.
розбивається на класи подібних матриць.
Отже,
всі матриці, які задають даний лінійний
оператор
![]() простору
простору![]() в різних базисах цього простору, подібні
між собою.
в різних базисах цього простору, подібні
між собою.
Якщо
матриця
![]() задає лінійний оператор
задає лінійний оператор![]() в базисі
в базисі![]() ,
то і будь-яка матриця
,
то і будь-яка матриця![]() подібна матриці
подібна матриці![]() :
:
![]()
також
задає оператор
![]() в деякому базисі
в деякому базисі![]() ,
а саме в базисі
,
а саме в базисі![]() ,
пов’язаному з базисом
,
пов’язаному з базисом![]() матрицею переходу
матрицею переходу![]() .
.
Отже,
всі матриці класа подібних матриць і
тільки вони задають в різних базисах
простору
![]() один і той же лінійний оператор цього
простору.
один і той же лінійний оператор цього
простору.
Властивості подібних матриць:
Подібні матриці мають рівні визначники.
Подібні матриці
 і
і або одночасно вироджені, або одночасно
невироджені.
або одночасно вироджені, або одночасно
невироджені.
Нехай
![]() і
і![]() – деякі лінійні оператори простору
– деякі лінійні оператори простору![]() .
.
Означення.
Оператор
 ,
який кожному вектору
,
який кожному вектору ставить у відповідність вектор
ставить у відповідність вектор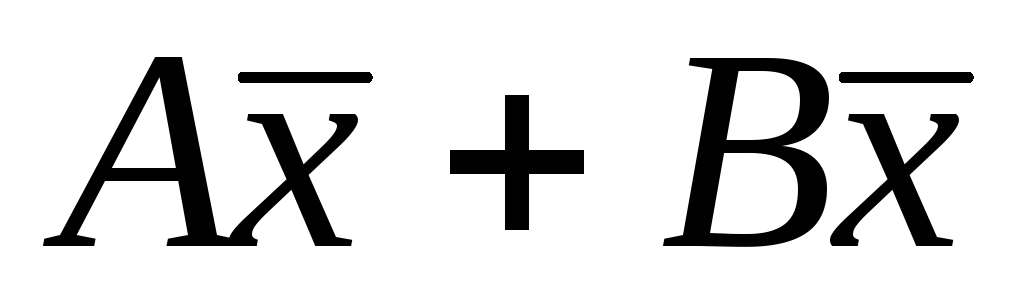 ,
називається сумою операторів
,
називається сумою операторів і
і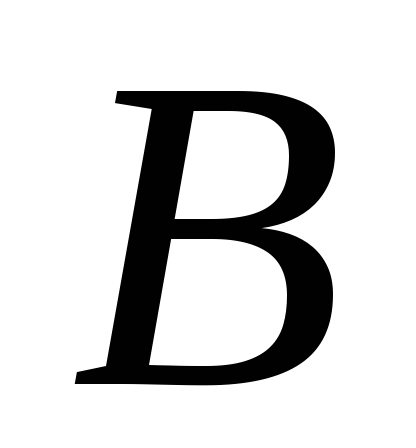 ,
позначається
,
позначається .
Отже,
.
Отже, означає, що
означає, що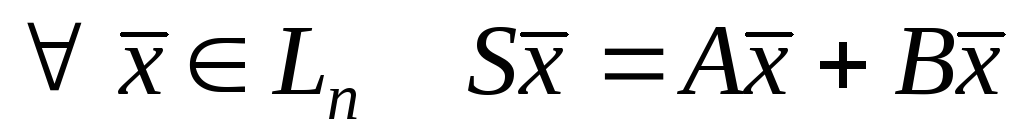 .
.Добутком лінійних операторів
 і
і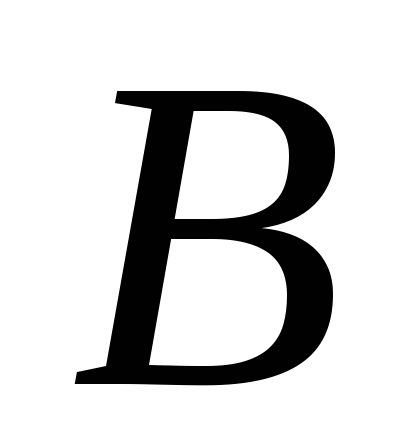 називається оператор
називається оператор ,
який визначається за формулою:
,
який визначається за формулою: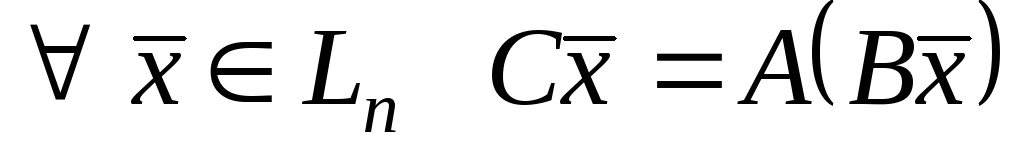 ,
позначається
,
позначається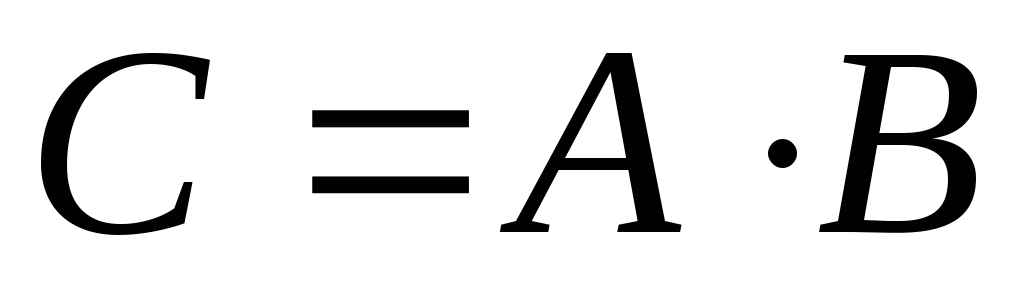 .
.Добутком лінійного оператора
 на число
на число називається оператор
називається оператор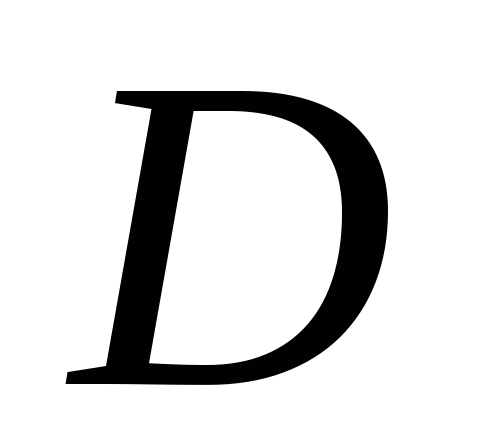 ,
який визначається за формулою:
,
який визначається за формулою: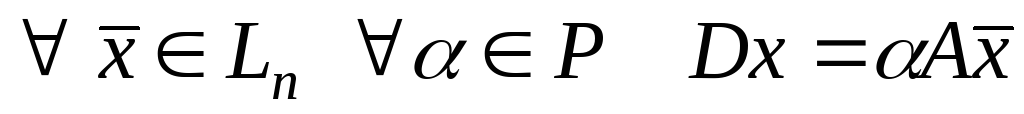 ,
позначають
,
позначають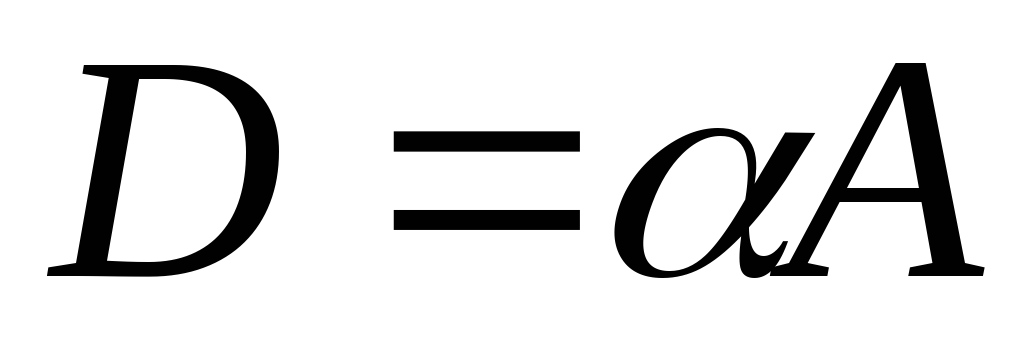 .
.
Властивості операцій над лінійними операторами:
Сума лінійних операторів
 і
і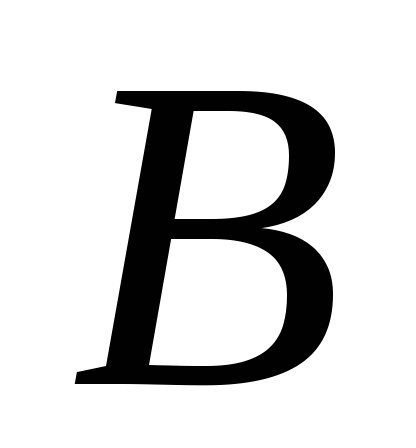 є лінійним оператором.
є лінійним оператором.Операція додавання лінійних операторів асоціативна і комутативна.
Множина
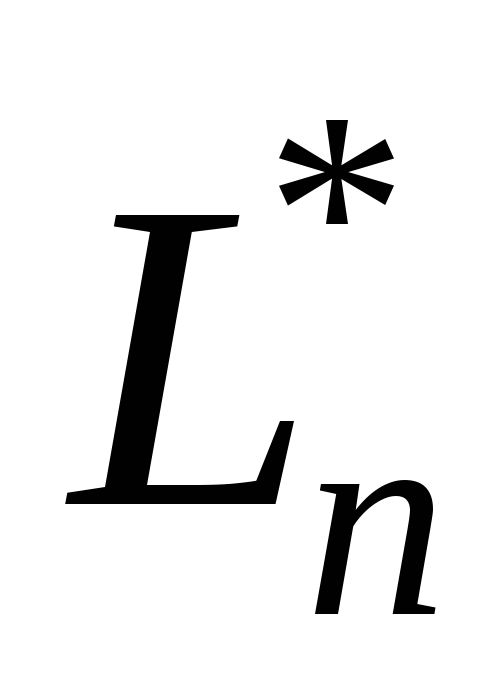 всіх лінійних операторів простору
всіх лінійних операторів простору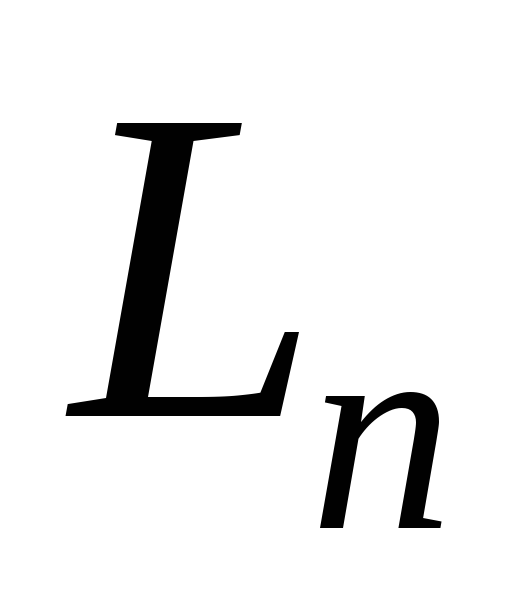 з визначеною на ній операцією додавання
є адитивною абелевою групою.
з визначеною на ній операцією додавання
є адитивною абелевою групою.Добуток лінійних операторів
 і
і є лінійним оператором.
є лінійним оператором.Операція множення операторів асоціативна і пов’язана з операцією додавання дистрибутивними законами.
Множина
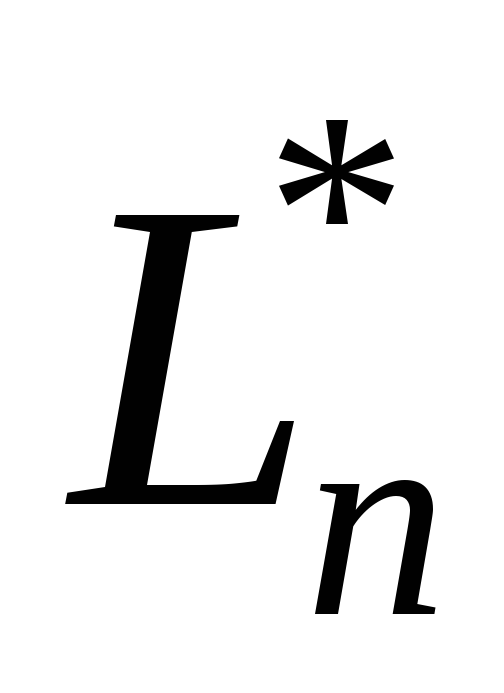 всіх лінійних операторів простору
всіх лінійних операторів простору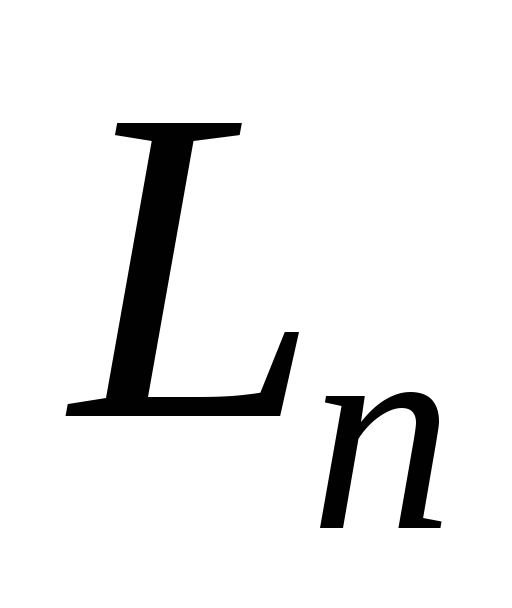 з визначеними на ній операціями додавання
і множення є кільцем.
з визначеними на ній операціями додавання
і множення є кільцем.Добуток лінійного оператора
 на число
на число є лінійним оператором.
є лінійним оператором.Множина
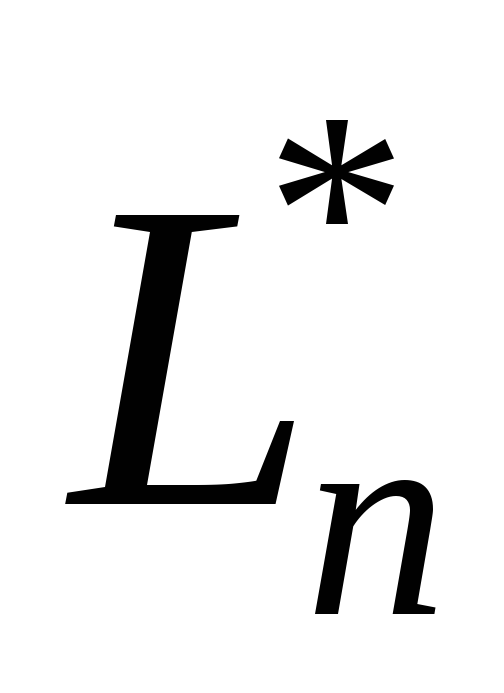 всіх лінійних операторів простору
всіх лінійних операторів простору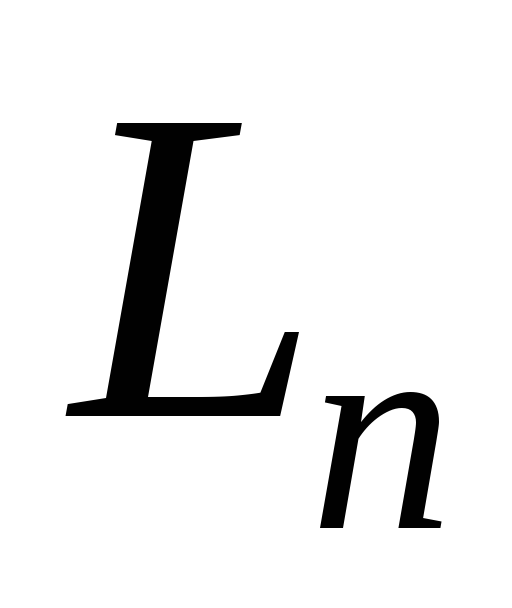 є лінійним простором над полем
є лінійним простором над полем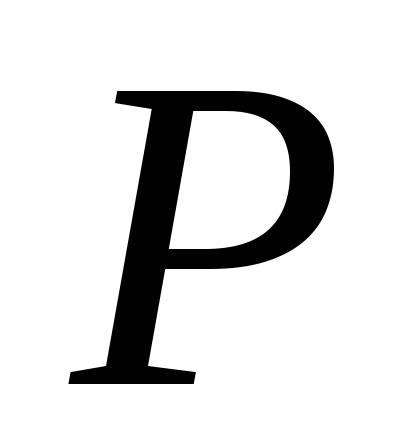 .
.
Множина
![]() з визначеними на ній операціями є
прикладом алгебраїчної системи, яка
називаєтьсялінійною
алгеброю
або просто алгеброю.
Лінійна алгебра, так само як група,
кільце і поле, належить до основних
типів алгебраїчних систем.
з визначеними на ній операціями є
прикладом алгебраїчної системи, яка
називаєтьсялінійною
алгеброю
або просто алгеброю.
Лінійна алгебра, так само як група,
кільце і поле, належить до основних
типів алгебраїчних систем.
Означення.
Лінійною алгеброю над полем
![]() називається множина
називається множина![]() ,
на якій визначені операції додавання
і множення і операція множення елементів
з
,
на якій визначені операції додавання
і множення і операція множення елементів
з![]() на елементи з поля
на елементи з поля![]() ,
причому
,
причому![]() відносно додавання і множення елементів
з
відносно додавання і множення елементів
з![]() є кільце, а відносно додавання та множення
на елементи з
є кільце, а відносно додавання та множення
на елементи з![]() – лінійний простір і, зокрема, множення
елементів з
– лінійний простір і, зокрема, множення
елементів з![]() і множення на елементи з
і множення на елементи з![]() пов’язані співвідношеннями
пов’язані співвідношеннями
![]()
Лінійні
алгебри
![]() і
і![]() над полем
над полем![]() називаються ізоморфними, якщо між їх
елементами можна встановити взаємно
однозначну відповідність так, що якщо
елементам
називаються ізоморфними, якщо між їх
елементами можна встановити взаємно
однозначну відповідність так, що якщо
елементам![]() і
і![]() алгебри
алгебри![]() відповідають елементи
відповідають елементи![]() і
і![]() алгебри
алгебри![]() ,
то сумі
,
то сумі![]() відповідає сума
відповідає сума![]() ,
добутку
,
добутку![]() – добуток
– добуток![]() і добутку
і добутку![]() відповідає добуток
відповідає добуток![]() .
.
Теорема.
Алгебра
![]() лінійних операторів
лінійних операторів![]() вимірного
векторного простору
вимірного
векторного простору![]() над полем
над полем![]() ізоморфна алгебрі
ізоморфна алгебрі![]() матриць
матриць![]() ого
порядку над полем
ого
порядку над полем![]() .
.
Нехай
![]() – деяка підмножина
– деяка підмножина![]() вимірного
лінійного простору
вимірного
лінійного простору![]() і
і![]() - довільний лінійний оператор цього
простору. Оператор
- довільний лінійний оператор цього
простору. Оператор![]() переводить кожний вектор
переводить кожний вектор![]() в деякий вектор
в деякий вектор![]() ,
який є образом вектора
,
який є образом вектора![]() .
.
Означення.
Сукупність образів всіх векторів множини
![]() називається образом множини
називається образом множини![]() відносно оператора
відносно оператора![]() ,
позначають
,
позначають![]() .
.
Теорема
1.
Образ будь-якого лінійного підпростору
![]() простору
простору![]() відносно будь-якого лінійного оператора
відносно будь-якого лінійного оператора![]() також є підпростором простору
також є підпростором простору![]() .
.
Означення.
Сукупність
![]() образів усіх векторів простору
образів усіх векторів простору![]() називається областю значень лінійного
оператора
називається областю значень лінійного
оператора![]() .
.
Іноді
область значень лінійного оператора
![]() називають образом оператора
називають образом оператора![]() і позначають символом
і позначають символом![]() .
З теореми 1 випливає, що образ лінійного
оператора
.
З теореми 1 випливає, що образ лінійного
оператора![]() є лінійним підпростором простору
є лінійним підпростором простору![]() .
.
Означення.
Розмірність області значень
![]() називають рангом оператора
називають рангом оператора![]() і позначають
і позначають![]() .
.
Теорема
2.
Ранг будь-якого лінійного оператора
простору
![]() дорівнює рангу матриці цього оператора
у довільно обраному базисі.
дорівнює рангу матриці цього оператора
у довільно обраному базисі.
Але
розмірність підпростору
![]() ,
тобто ранг оператора
,
тобто ранг оператора![]() ,
дорівнює максимальній кількості лінійно
незалежних векторів системи (*), отже –
рангу матриці
,
дорівнює максимальній кількості лінійно
незалежних векторів системи (*), отже –
рангу матриці![]() .
.
Наслідок. Всі подібні між собою матриці мають однакові ранги.
Означення.
Ядром лінійного оператора
![]() простору
простору![]() називається сукупність всіх векторів
цього простору, які оператором
називається сукупність всіх векторів
цього простору, які оператором![]() відображаються в нульовий вектор
відображаються в нульовий вектор![]() .
.
Ядро
лінійного оператора позначається
символом
![]() .
.
Розмірність
ядра оператора
![]() називаєтьсядефектом
цього оператора.
називаєтьсядефектом
цього оператора.
Ядро
лінійного оператора є підпростором
простору
![]() .
.
Теорема
3.
Сума рангу і дефекту лінійного оператора
![]() простору
простору![]() дорівнює розмірності
дорівнює розмірності![]() цього простору
цього простору
![]() .
.
Нехай
![]() – лінійний оператор, що діє в
– лінійний оператор, що діє в![]() вимірному
просторі
вимірному
просторі![]() .
.
Означення.
Лінійний оператор
![]() простору
простору![]() називається не виродженим, якщо його
ранг дорівнює
називається не виродженим, якщо його
ранг дорівнює![]() ;
оператор
;
оператор![]() називається виродженим, якщо його ранг
менше
називається виродженим, якщо його ранг
менше![]() .
.
Отже,
лінійний оператор
![]() не вироджений якщо:
не вироджений якщо:
область значень
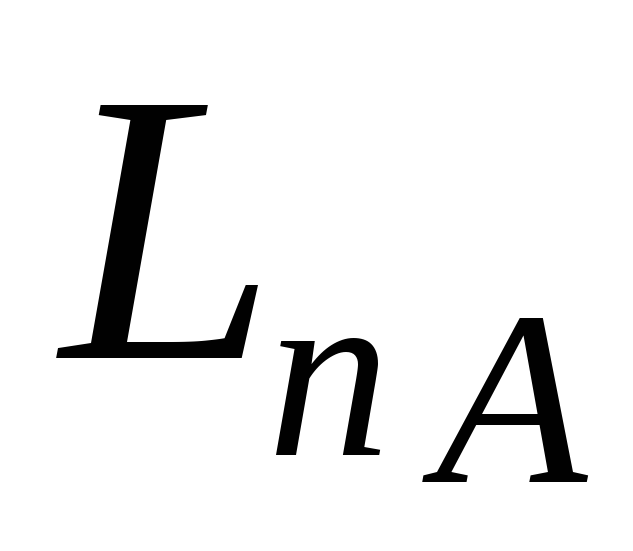 оператора
оператора співпадає з простором
співпадає з простором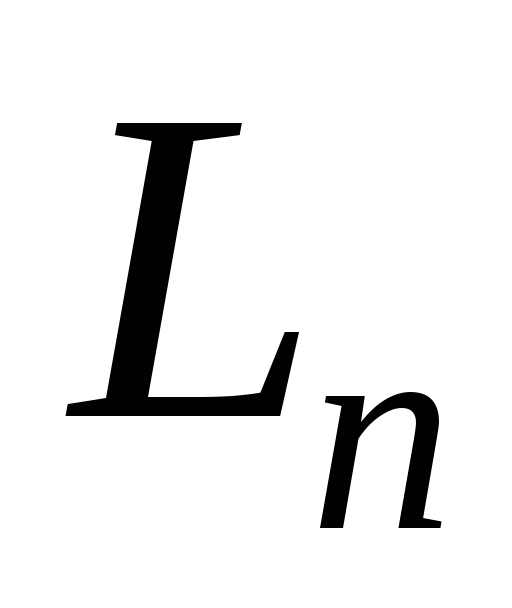 ;
;дефект оператора дорівнює нулю;
ядро оператора
 складається тільки з нульового вектора.
складається тільки з нульового вектора.
Теорема
4.
Лінійний оператор
![]() простору
простору![]() не вироджений тоді і тільки тоді, коли
його матриця
не вироджений тоді і тільки тоді, коли
його матриця![]() в довільно вибраному базисі
в довільно вибраному базисі![]() простору
простору![]() невироджена.
невироджена.
Теорема
5.
Не вироджений лінійний оператор
![]() простору
простору![]() взаємно однозначно відображає простір
взаємно однозначно відображає простір![]() на весь
на весь![]() .
.
Теорема
6.
Не вироджений лінійний оператор
![]() простору
простору![]() будь-яку лінійно незалежну систему
векторів цього простору переводить в
лінійно незалежну систему.
будь-яку лінійно незалежну систему
векторів цього простору переводить в
лінійно незалежну систему.
Означення.
Лінійний оператор
![]() простору
простору![]() називається оберненим до лінійного
простору
називається оберненим до лінійного
простору![]() ,
якщо
,
якщо![]() ,
де
,
де![]() – одиничний оператор. Обернений оператор
позначають
– одиничний оператор. Обернений оператор
позначають![]() .
.
Обернений
оператор переводить кожний вектор
![]() у вектор
у вектор![]() .
.
Теорема
7.
Для того щоб існував оператор
![]() ,
обернений до оператора
,
обернений до оператора![]() ,
необхідно і достатньо, щоб оператор
,
необхідно і достатньо, щоб оператор![]() був невиродженим.
був невиродженим.
Доведення:
Взаємно обернені оператори
![]() і
і![]() задаються в будь-якому фіксованому
базисі
задаються в будь-якому фіксованому
базисі![]() простору
простору![]() взаємно оберненими матрицями
взаємно оберненими матрицями![]() і
і![]() і, навпаки, взаємно обернені матриці
і, навпаки, взаємно обернені матриці![]() і
і![]() задають в цьому базисі взаємно обернені
оператори
задають в цьому базисі взаємно обернені
оператори![]() і
і![]() .
.
Достатність
умови.
Припустимо, що оператор
![]() – невироджений. Тоді в деякому базисі
простору
– невироджений. Тоді в деякому базисі
простору![]() він задається невиродженою матрицею
він задається невиродженою матрицею![]() ,
для якої існує обернена матриця
,
для якої існує обернена матриця![]() .
Ця обернена матриця задає в базисі
.
Ця обернена матриця задає в базисі![]() оператор
оператор![]() ,
обернений до оператора
,
обернений до оператора![]() .
.
Необхідність
умови.
Нехай для оператора
![]() існує обернений оператор
існує обернений оператор![]() .
Тоді для матриці
.
Тоді для матриці![]() оператора
оператора![]() в базисі
в базисі![]() існує обернена матриця
існує обернена матриця![]() .
Тому матриця
.
Тому матриця![]() – невироджена та оператор
– невироджена та оператор![]() – невироджений.
– невироджений.
З теореми випливає ще одне означення невиродженого оператора, а саме: невиродженим лінійним оператором називається лінійний оператор, для якого існує обернений оператор.
Ненульовий
вектор
![]() називаєтьсявласним
вектором оператора,
якщо
називаєтьсявласним
вектором оператора,
якщо
![]() .
В цьому випадку
.
В цьому випадку![]() називаєтьсявласним
числом (значенням) оператора
називаєтьсявласним
числом (значенням) оператора
![]() .
.
Запишемо характеристичний многочлен оператора:
![]() .
.
Теорема.
Число
![]() буде власним числом оператора
буде власним числом оператора![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли![]() .
.
Алгебраїчною
кратністю власного
значення
![]() називається таке число
називається таке число![]() ,
при якому характеристичний многочлен
,
при якому характеристичний многочлен![]() ділиться на
ділиться на![]() і не ділиться на
і не ділиться на![]() .
Іншими словами, це кратність числа
.
Іншими словами, це кратність числа![]() як кореня характеристичного многочлена.Геометрична
кратність
як кореня характеристичного многочлена.Геометрична
кратність
![]() – це розмірність інваріантного
підпростору
– це розмірність інваріантного
підпростору![]() ,
тобто кількість лінійно незалежних
власних векторів, що відповідають
власному значенню
,
тобто кількість лінійно незалежних
власних векторів, що відповідають
власному значенню![]() .
.
Нехай
лінійний оператор
![]()
![]() вимірного
векторного простору
вимірного
векторного простору![]() має
має![]() лінійно незалежних власних векторів
лінійно незалежних власних векторів![]() ,
тобто в просторі
,
тобто в просторі![]() існує базис
існує базис![]() ,
який складається з власних векторів
оператора
,
який складається з власних векторів
оператора![]() з власними значеннями
з власними значеннями![]() .
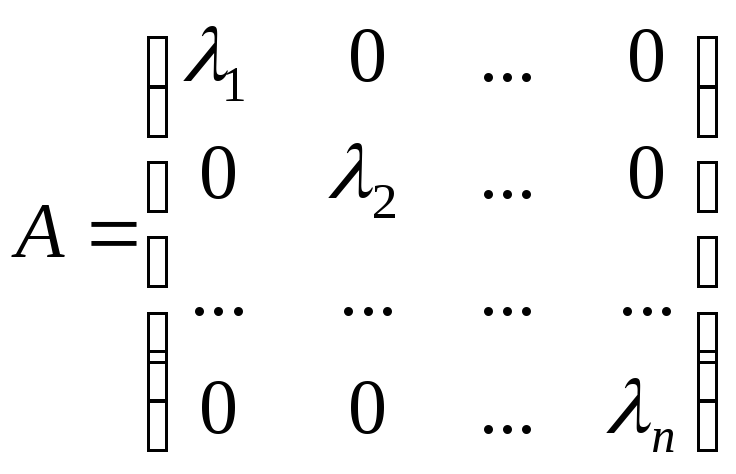
Тоді
.
Тоді![]() В цьому базисі оператор
В цьому базисі оператор![]() задається діагональною матрицею:
задається діагональною матрицею:
 .
.
Навпаки,
якщо в деякому базисі
![]() матриця
матриця![]() оператора
оператора![]() діагональна
діагональна
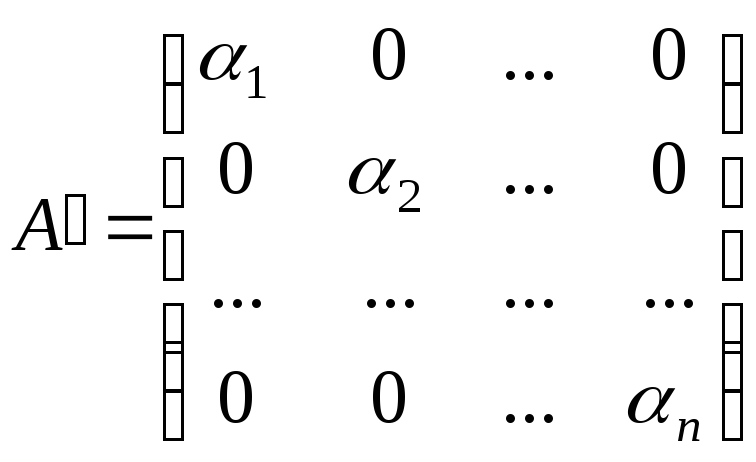 ,
,
то
![]() ,
тобто всі вектори цього базису – власні
вектори оператора
,
тобто всі вектори цього базису – власні
вектори оператора![]() .
.
Отже, справедлива теорема.
Теорема.
Якщо вектори базису
![]() є власними векторами лінійного оператора
є власними векторами лінійного оператора![]() ,
то в базисі
,
то в базисі![]() оператор
оператор![]() задається діагональною матрицею.
Навпаки, якщо в деякому базисі матриця
оператора
задається діагональною матрицею.
Навпаки, якщо в деякому базисі матриця
оператора![]() – діагональна, то всі вектори цього
базису є власними векторами оператора
– діагональна, то всі вектори цього
базису є власними векторами оператора![]() .
.
Виникає
питання: чи можна оператор
![]() задати в деякому базисі діагональною
матрицею, і як, знаючи матрицю оператора
задати в деякому базисі діагональною
матрицею, і як, знаючи матрицю оператора![]() в деякому базисі, встановити, чи має цей
оператор власні вектори, які утворюють
базис простору?
в деякому базисі, встановити, чи має цей
оператор власні вектори, які утворюють
базис простору?
Означення.
Лінійний оператор
![]() в
в![]() вимірному
просторі
вимірному
просторі![]() над полем
над полем![]() має простий спектр, якщо в полі
має простий спектр, якщо в полі![]() існує
існує![]() різних характеристичних коренів цього
оператора.
різних характеристичних коренів цього
оператора.
Теорема.
Якщо лінійний оператор
![]() має простий спектр, то існує базис
простору
має простий спектр, то існує базис
простору![]() ,
в якому цей оператор задається діагональною
матрицею.
,
в якому цей оператор задається діагональною
матрицею.
Доведення.
За умовою теореми оператор
![]() має в полі
має в полі![]()
![]() різних характеристичних коренів
різних характеристичних коренів![]() ,
які є власними значеннями оператора
,
які є власними значеннями оператора![]() ,
а тому існують власні вектори
,
а тому існують власні вектори![]() такі, що
такі, що![]() .
Оскільки власні значення
.
Оскільки власні значення![]() – різні, то вектори
– різні, то вектори![]() – лінійно незалежні, отже утворюють
базис простору
– лінійно незалежні, отже утворюють
базис простору![]() .
В цьому базисі оператор
.
В цьому базисі оператор![]() задається діагональною матрицею:
задається діагональною матрицею:
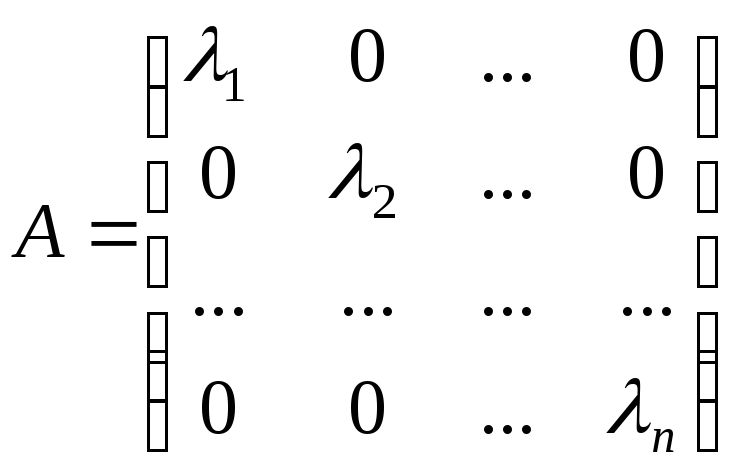 .
.
Теорему доведено.
Нехай
![]() матриця
матриця![]() ого
порядку над полем
ого
порядку над полем![]() .
Вважають, що матриця
.
Вважають, що матриця![]() зводиться до діагонального виду, якщо
існує діагональна матриця, подібна до
матриці
зводиться до діагонального виду, якщо
існує діагональна матриця, подібна до
матриці![]() .
.
Теорема.
Кожна матриця
![]() ого
порядку над полем
ого
порядку над полем![]() ,
яка має в цьому полі
,
яка має в цьому полі![]() різних характеристичних коренів, подібна
деякій діагональній матриці, тобто
зводиться до діагонального виду.
різних характеристичних коренів, подібна
деякій діагональній матриці, тобто
зводиться до діагонального виду.
Доведення.
Нехай
![]() – матриця
– матриця![]() ого
порядку над полем
ого
порядку над полем![]() ,
,![]() – її характеристичні корені, всі вони
різні і належать полю
– її характеристичні корені, всі вони
різні і належать полю![]() .
.
Знайдемо
матрицю
![]() подібну матриці
подібну матриці![]() .
.
Для
цього в
![]() вимірному
просторі
вимірному
просторі![]() над полем
над полем![]() виберемо базис
виберемо базис![]() ,
в якому лінійний оператор
,
в якому лінійний оператор![]() задається матрицею
задається матрицею![]() .
Оскільки всі характеристичні корені
матриці
.
Оскільки всі характеристичні корені
матриці![]() різні і належать полю
різні і належать полю![]() ,
то оператор
,
то оператор![]() має простий спектр
має простий спектр![]() .
Тому існує базис
.
Тому існує базис![]() простору
простору![]() ,
в якому оператор
,
в якому оператор![]() задається діагональною матрицею
задається діагональною матрицею
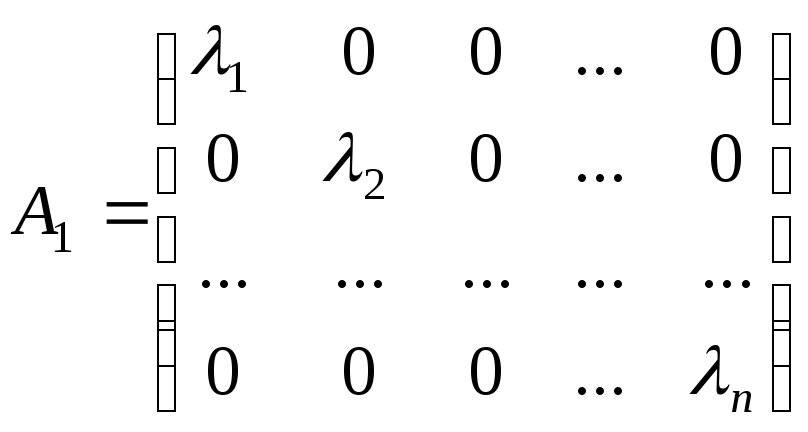 .
.
Матриці
![]() і
і![]() подібні, оскільки вони задають один і
той же оператор
подібні, оскільки вони задають один і
той же оператор![]() .
Теорему доведено.
.
Теорему доведено.
Знаходження
матриці, подібної матриці
![]() ,
називається зведенням матриці
,
називається зведенням матриці![]() до діагонального виду.
до діагонального виду.
Розглянемо
спосіб знаходження діагональної матриці
![]() ,
подібної матриці
,
подібної матриці![]() .
.
Вище
було доведено, що матриця
![]() лінійного оператора
лінійного оператора![]() векторного простору
векторного простору![]() над полем
над полем![]() у деякому базисі є діагональною тоді і
тільки тоді, коли цей базис складається
з власних векторів даного оператора.
у деякому базисі є діагональною тоді і
тільки тоді, коли цей базис складається
з власних векторів даного оператора.
Достатньою умовою для зведення матриці лінійного оператора векторного простору розмірності
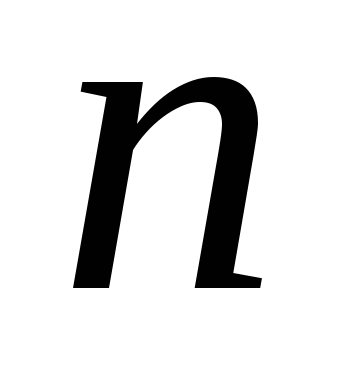 є наявність у даного оператора
є наявність у даного оператора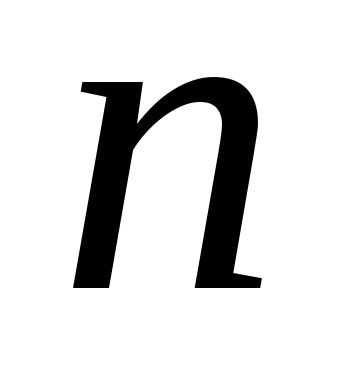 різних власних значень, причому
діагональними елементами будуть саме
ці власні значення.
різних власних значень, причому
діагональними елементами будуть саме
ці власні значення.Якщо лінійний оператор має менш як
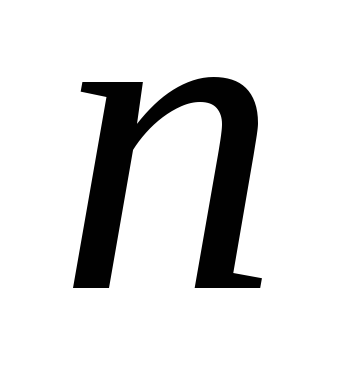 власних значень, причому враховується
їх кратність як коренів характеристичного
рівняння оператора, то матриця такого
оператора не зводиться до діагонального
виду.
власних значень, причому враховується
їх кратність як коренів характеристичного
рівняння оператора, то матриця такого
оператора не зводиться до діагонального
виду.Якщо лінійний оператор має менш як
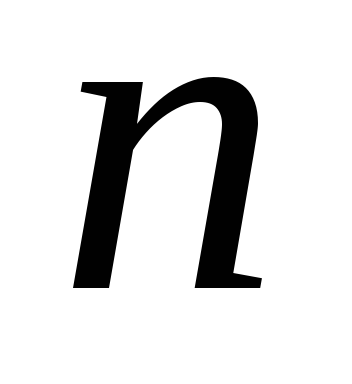 різних власних значень, причому
враховуються кратності кожного як
коренів характеристичного рівняння
оператора (їх рівно
різних власних значень, причому
враховуються кратності кожного як
коренів характеристичного рівняння
оператора (їх рівно ),
то треба дослідити ще, яке число
),
то треба дослідити ще, яке число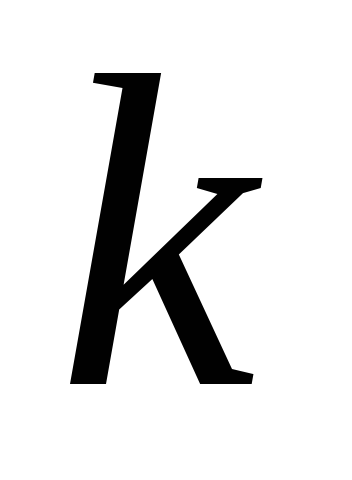 лінійно незалежних власних векторів
визначає кожен корінь
лінійно незалежних власних векторів
визначає кожен корінь кратності
кратності .
Оскільки число лінійно незалежних
власних векторів довільного лінійного
оператора, які належать одному власному
значенню
.
Оскільки число лінійно незалежних
власних векторів довільного лінійного
оператора, які належать одному власному
значенню ,
не перевищує
,
не перевищує ,
то
,
томатриця не зводиться до діагонального виду, коли хоча б для одного
 виконується нерівність
виконується нерівність (тоді не набереться стільки власних
векторів, скільки їх повинно бути в
базисі);
(тоді не набереться стільки власних
векторів, скільки їх повинно бути в
базисі);матриця зводиться до діагонального виду, коли для всіх
 виконується рівність
виконується рівність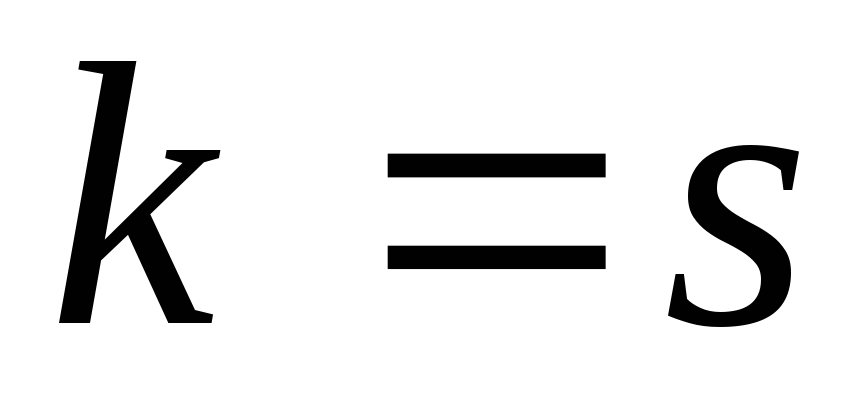 ,
причому діагональними елементами є
власні значення оператора, що повторюються
стільки разів, яка їх кратність.
,
причому діагональними елементами є
власні значення оператора, що повторюються
стільки разів, яка їх кратність.
Серед лінійних операторів, які діють в евклідовому просторі, важливу роль відіграють ортогональні та симетричні оператори. Розглянемо питання щодо ортогональних операторів.
Означення.
Лінійний оператор
![]() в дійсному евклідовому просторі
в дійсному евклідовому просторі![]() називається ортогональним, якщо
називається ортогональним, якщо![]()
![]() .
.
Ортогональний оператор зберігає скалярний добуток, отже, він зберігає довжини векторів і кути між ними.
Властивості ортогональних векторів:
Тотожній оператор
 є ортогональним, оскільки
є ортогональним, оскільки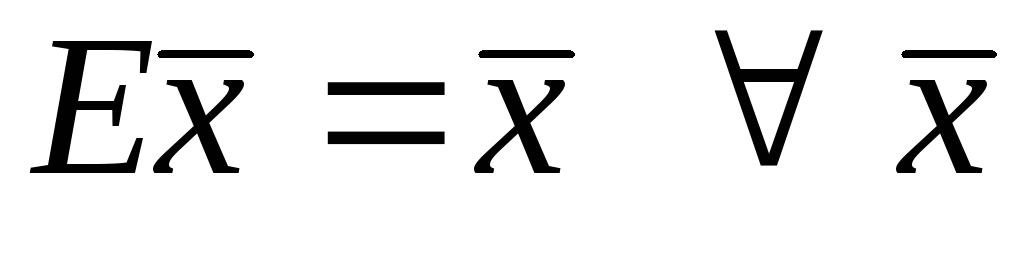 ,
отже,
,
отже,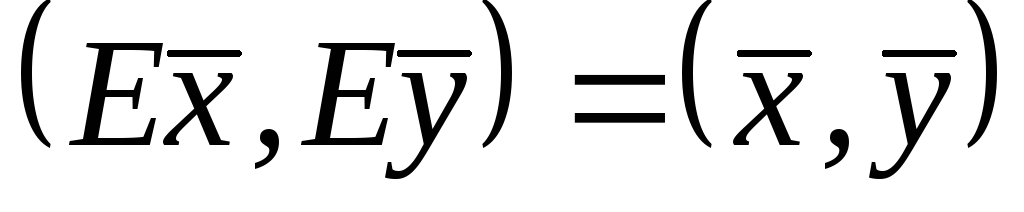 .
.Добуток ортогональних операторів є ортогональним, оскільки оператори
 і
і ортогональні, то
ортогональні, то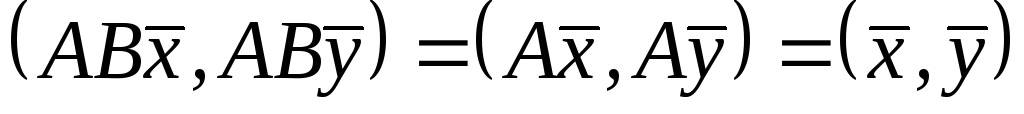 .
.Оператор, обернений до ортогонального оператору, є ортогональним.
Якщо
 – ортогональний оператор, то добуток
– ортогональний оператор, то добуток буде ортогональним тоді і тільки тоді,
коли
буде ортогональним тоді і тільки тоді,
коли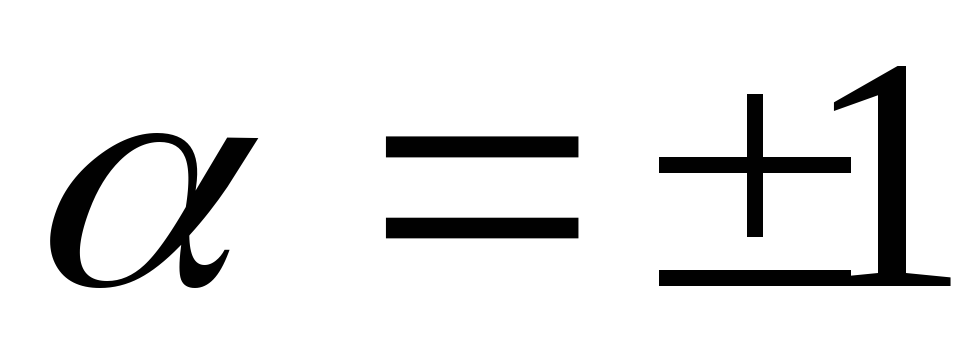 .
Це випливає з рівності
.
Це випливає з рівності .
.
Ортогональний
оператор переводить будь-який
ортонормований базис в ортонормований.
Покажемо, що вірне і обернене твердження:
лінійний оператор
![]() ,
який переводить хоч би один ортонормований
базис в ортонормований є ортогональним.
,
який переводить хоч би один ортонормований
базис в ортонормований є ортогональним.
Дійсно,
нехай ортонормований базис
![]() оператором
оператором![]() переводиться в ортонормований базис
переводиться в ортонормований базис![]() .
Тоді, якщо
.
Тоді, якщо
![]() ,
,
![]() ,
,
то
![]() ,
,
![]()
і
![]() .
.
Нехай
![]() – матриця ортогонального оператора в
ортогональному базисі
– матриця ортогонального оператора в
ортогональному базисі![]() .
Оскільки під дією ортогонального
оператора ортонормований базис переходить
в ортонормований, то образи
.
Оскільки під дією ортогонального
оператора ортонормований базис переходить
в ортонормований, то образи
![]() базисних векторів
базисних векторів
![]() самі утворюють ортонормований базис.
Отже,
самі утворюють ортонормований базис.
Отже,
![]() при
при![]() і
і![]() при всіх
при всіх![]() ,
тобто
,
тобто
![]() при
при
![]() ,
,
![]() при всіх
при всіх
![]() . (1)
. (1)
Звідси
випливає, що стовпці матриці
![]() ,
які розглядаються як вектори, самі
утворюють ортонормовану систему. Це ж
вірно і для рядків, тобто
,
які розглядаються як вектори, самі
утворюють ортонормовану систему. Це ж
вірно і для рядків, тобто
![]() при
при
![]() ,
,
![]() при всіх
при всіх
![]() . (2)
. (2)
Означення.
Матриця
![]() ,
для якої транспонована матриця
,
для якої транспонована матриця![]() співпадає з оберненою матрицею
співпадає з оберненою матрицею![]() називається ортогональною матрицею.
називається ортогональною матрицею.
Отже,
якщо для матриці
![]() має місце співвідношення
має місце співвідношення![]() ,
то матриця
,
то матриця![]() – ортогональна і для неї виконуються
рівності (1) і (2).
– ортогональна і для неї виконуються
рівності (1) і (2).
Матриця
ортогонального оператора в будь-якому
базисі є ортогональною, і, навпаки, якщо
в деякому ортонормованому базисі матриця
оператору
![]() є ортогональною, то і оператор
є ортогональною, то і оператор![]() – ортогональний.
– ортогональний.
Теорема
1.
Визначник ортогональної матриці дорівнює
![]() .
.
Доведення.
Із рівності
![]() випливає, що
випливає, що![]() .
Але, оскільки
.
Але, оскільки![]() ,
то
,
то![]() і
і![]() .
Теорему доведено.
.
Теорему доведено.
З теореми
випливає, що будь-який ортогональний
оператор є невиродженим. Обернене
твердження невірне, оскільки не будь-яка
матриця з визначником, що дорівнює
![]() ,
буде ортогональною.
,
буде ортогональною.
Теорема 2. Матриця переходу від ортонормованого базису евклідового простору до іншого його ортонормованого базису є ортогональною.
Доведення.
Нехай в евклідовому просторі
![]() задані два ортонормованих базиси:
задані два ортонормованих базиси:![]() і
і
![]() з матрицею переходу
з матрицею переходу![]() ,
тобто
,
тобто![]() .
.
Оскільки
базис
![]() ортонормований, то скалярний добуток
будь-яких двох векторів, зокрема будь-яких
векторів з базису
ортонормований, то скалярний добуток
будь-яких двох векторів, зокрема будь-яких
векторів з базису![]() ,
дорівнює сумі добутків відповідних
координат цих векторів в базисі
,
дорівнює сумі добутків відповідних
координат цих векторів в базисі![]() .
.
За умовою
і базис
![]() ортонормований, тому скалярний квадрат
кожного вектора з
ортонормований, тому скалярний квадрат
кожного вектора з![]() дорівнює одиниці, а скалярний добуток
будь-яких двох різних векторів з
дорівнює одиниці, а скалярний добуток
будь-яких двох різних векторів з![]() дорівнює нулю. Звідси для рядків координат
базису
дорівнює нулю. Звідси для рядків координат
базису![]() в базисі
в базисі![]() ,
тобто для рядків матриці
,
тобто для рядків матриці![]() ,
випливають твердження, справедливі для
ортогональної матриці. Отже, матриця
,
випливають твердження, справедливі для
ортогональної матриці. Отже, матриця![]() – ортогональна матриця. Теорему доведено.
– ортогональна матриця. Теорему доведено.
Теорема
3.
Власні значення ортогонального оператору
дорівнюють
![]() .
.
Доведення.
Нехай
![]() – власний вектор і
– власний вектор і![]() – відповідне до нього власне значення
ортогонального оператора
– відповідне до нього власне значення
ортогонального оператора![]() .
Тоді
.
Тоді![]() ,
,
звідки
одержуємо (оскільки
![]() )
)![]() і
і![]() .
Теорему доведено.
.
Теорему доведено.
З’ясуємо,
що собою являє довільний ортогональний
оператор, який діє в дійсному
![]() вимірному
евклідовому просторі. Нехай
вимірному
евклідовому просторі. Нехай![]() – ортогональне перетворення прямої
– ортогональне перетворення прямої![]() і
і![]() .
Тоді
.
Тоді![]() ,
і, отже,
,
і, отже,![]() ,
де
,
де![]() ,
тобто
,
тобто![]() ,
і
,
і![]() – або тотожнє перетворення, або центральна
симетрія.
– або тотожнє перетворення, або центральна
симетрія.
Нехай
тепер
![]() – ортогональне перетворення площини
– ортогональне перетворення площини![]() і
і
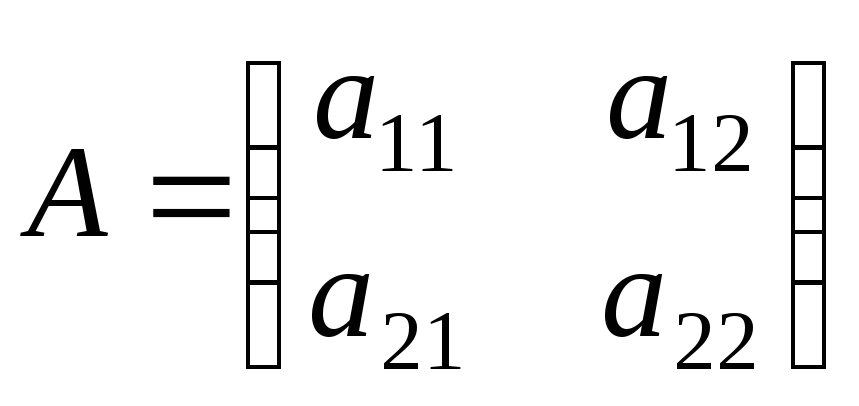
– його матриця в деякому ортонормованому базисі. Тоді
![]() ;
;
![]() ;
;![]() .
.
В силу
перших двох рівностей знайдуться такі
![]() і
і![]() ,
що
,
що![]() ,
,![]() і
і![]() ,
,![]() .
Тоді третя рівність дає
.
Тоді третя рівність дає
![]() .
.
Звідси
випливає, що
![]() або
або![]() .
В першому випадку
.
В першому випадку![]() ,
,![]() ,
і одержуємо
,
і одержуємо
![]() ,
,
тобто
перетворення
![]() – це поворот на кут
– це поворот на кут![]() навколо початку координат. (зокрема при
навколо початку координат. (зокрема при![]() ,
це тотожнє перетворення, а при
,
це тотожнє перетворення, а при![]() – симетрія відносно початку координат).
– симетрія відносно початку координат).
У другому
випадку
![]() ,
,![]() і
і
![]() .
.
Ця
матриця симетрична і ортогональна, і в
деякому ортонормованому базисі
![]() зводиться до діагонального виду. Власні
значення знаходяться безпосередньо з
рівняння
зводиться до діагонального виду. Власні
значення знаходяться безпосередньо з
рівняння
![]() ,
,
тобто
![]() ,
і матриця перетворення
,
і матриця перетворення![]() зводиться до виду
зводиться до виду
![]() .
.
Довільний
вектор
![]() ,
що дорівнює в новому базисі
,
що дорівнює в новому базисі![]() ,
перетворюється в
,
перетворюється в![]() .
Це симетрія відносно прямої, що
визначається вектором
.
Це симетрія відносно прямої, що
визначається вектором![]() – першим базисним вектором нового
базису (рис. 1).
– першим базисним вектором нового
базису (рис. 1).
О тже,
ортогональне перетворення площини –
це або його поворот навколо початку
координат на деякий кут
тже,
ортогональне перетворення площини –
це або його поворот навколо початку
координат на деякий кут![]() (зокрема, тотожнє перетворення або
центральна симетрія; визначник такого
перетворення дорівнює +1), або – осьова
симетрія (з визначником, що дорівнює
‑1).
(зокрема, тотожнє перетворення або
центральна симетрія; визначник такого
перетворення дорівнює +1), або – осьова
симетрія (з визначником, що дорівнює
‑1).
Із доведеного випливають дві теореми елементарної геометрії:
Добуток двох осьових симетрій є поворотом навколо точки перетину осей симетрії (оскільки це ортогональне перетворення з визначником, що дорівнює +1).
Добуток поворота і симетрії, вісь якої проходить через центр поворота, є симетрією відносно деякої нової осі, яка проходить через ту ж точку (оскільки це ортогональне перетворення з визначником, що дорівнює ‑1).
Означення.
Лінійний оператор
![]()
![]() вимірного
евклідового простору називається
симетричним (самоспряженим), якщо для
будь-яких векторів
вимірного
евклідового простору називається
симетричним (самоспряженим), якщо для
будь-яких векторів![]() цього простору виконується рівність:
цього простору виконується рівність:
![]() .
.
Тотожній
оператор
![]() та нульовий оператор
та нульовий оператор![]() є симетричними операторами.
є симетричними операторами.
Більш
загальним прикладом симетричного
оператора є оператор, при якому будь-який
вектор помножується на фіксоване число
![]() ,
,
![]() .
.
Дійсно,
![]() .
.
Теорема 1. Симетричний оператор евклідового простору в будь-якому ортонормованому базисі задається симетричною матрицею. Навпаки, якщо лінійний оператор евклідового простору хоч би в одному ортонормоваму базисі задається симетричною матрицею, то цей оператор симетричний.
Доведення.
Нехай симетричний оператор
![]() задається в ортонормованому базисі
задається в ортонормованому базисі![]() матрицею
матрицею![]() .
.
В ортонормованому базисі скалярний добуток двох векторів дорівнює сумі добутків відповідних координат цих векторів, отже,
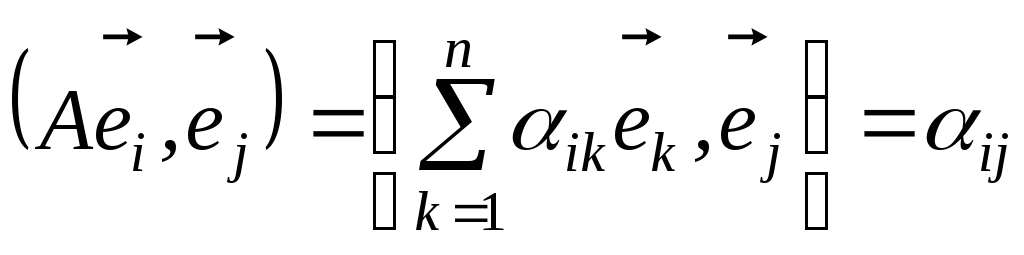 ,
,
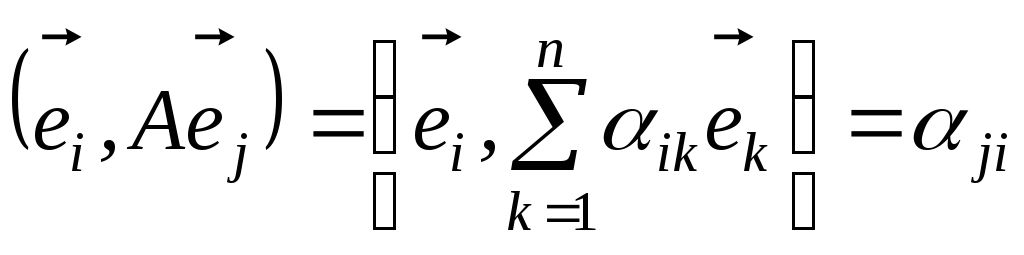 .
.
Оскільки
![]() – симетричний оператор, то
– симетричний оператор, то![]() для всіх
для всіх![]() ,
тобто матриця
,
тобто матриця![]() – симетрична.
– симетрична.
Навпаки,
нехай лінійний оператор
![]() ортонормованому базисі
ортонормованому базисі![]() задається симетричною матрицею
задається симетричною матрицею![]() ,
,![]() для всіх
для всіх![]() .
.
Якщо
![]() ,
,![]() – будь-які вектори простору, то
– будь-які вектори простору, то
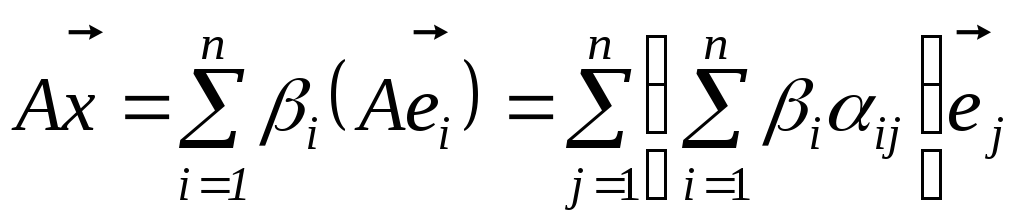 ;
;
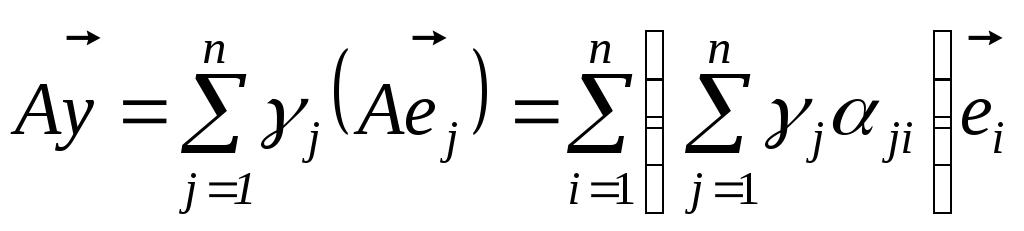 .
.
Оскільки
базис
![]() ортонормований, то
ортонормований, то
![]() ;
;
![]() ,
,
але
![]() ,
тому
,
тому![]() ,
тобто
,
тобто![]() .
.
Отже,
оператор
![]() – симетричний. Теорему доведено.
– симетричний. Теорему доведено.
Властивості симетричних операторів:
Сума симетричних операторів є симетричний оператор.
Добуток симетричного оператора на число є симетричний оператор.
Оператор, обернений до невиродженого симетричного оператора, є симетричним.
Для того, щоб добуток симетричних операторів
 і
і був симетричним, необхідно і достатньо,
щоб ці оператори були переставними,
тобто щоб виконувалась рівність
був симетричним, необхідно і достатньо,
щоб ці оператори були переставними,
тобто щоб виконувалась рівність .
.
Теорема 2. Всі характеристичні корені симетричного оператора дійсні.
Доведення. Оскільки характеристичні корені будь-якого лінійного оператора співпадають з характеристичними коренями матриці цього оператора в будь-якому базисі, а симетричний оператор задається в ортонормованих базисах симетричними матрицями, то достатньо довести наступне твердження. Всі характеристичні корені симетричної матриці – дійсні числа.
Нехай
![]() – характеристичний корінь симетричної
матриці
– характеристичний корінь симетричної
матриці![]() ,
,![]() .
Тоді система лінійних однорідних рівнянь
з комплексними коефіцієнтами
.
Тоді система лінійних однорідних рівнянь
з комплексними коефіцієнтами
![]()
має
нульовий визначник, отже має ненульовий
розв’язок
![]() ,
взагалі кажучи, комплексний.
,
взагалі кажучи, комплексний.
Отже,
![]() .
Помножимо обидві частини кожної
.
Помножимо обидві частини кожної![]() ої
рівності на
ої
рівності на![]() ,
одержимо
,
одержимо
![]() .
.
Додамо ліві і праві частини всіх одержаних рівностей, одержимо
![]() . (*)
. (*)
Коефіцієнт
при
![]() – відмінне від нуля дійсне число,
оскільки воно є сумою невід’ємних
дійсних чисел, хоча б одне з яких строго
додатнє. Дійсність
– відмінне від нуля дійсне число,
оскільки воно є сумою невід’ємних
дійсних чисел, хоча б одне з яких строго
додатнє. Дійсність![]() буде доведена, якщо доведемо дійсність
лівої частини рівності (*). Для цього
покажемо, що це комплексне число співпадає
зі своїм спряженим.
буде доведена, якщо доведемо дійсність
лівої частини рівності (*). Для цього
покажемо, що це комплексне число співпадає
зі своїм спряженим.
Використаємо
симетричність матриці
![]() .
.
![]() .
.
Теорему доведено.
Теорема
3.
Власні вектори симетричного оператора
![]() ,
яким відповідають різні власні значення
оператора, ортогональні.
,
яким відповідають різні власні значення
оператора, ортогональні.
Доведення.
Нехай
![]() – два власних значення симетричного
оператора
– два власних значення симетричного
оператора![]() ,
а
,
а![]() – відповідні до них власні вектори.
Тоді мають місце співвідношення
– відповідні до них власні вектори.
Тоді мають місце співвідношення
![]() ;
;
![]() .
.
Тому
![]() ;
;
![]() . (1)
. (1)
Оскільки
оператор
![]() – симетричний, то скалярні добутки
– симетричний, то скалярні добутки![]() і
і![]() дорівнюють між собою, тому з рівностей
(1) маємо
дорівнюють між собою, тому з рівностей
(1) маємо
![]() .
.
Оскільки
![]() ,
то звідси випливає, що
,
то звідси випливає, що![]() ,
тобто вектори
,
тобто вектори![]() і
і![]() ортогональні. Теорему доведено.
ортогональні. Теорему доведено.
Теорема
4.
Нехай
![]() – симетричний оператор в
– симетричний оператор в![]() ,
,![]() – його власний вектор. Сукупність
– його власний вектор. Сукупність![]() векторів
векторів![]() ,
ортогональних до вектора
,
ортогональних до вектора![]() ,
є
,
є![]() мірний
підпростір
мірний
підпростір![]() ,
інваріантний відносно оператора
,
інваріантний відносно оператора![]() .
.
Доведення.
Сукупність
![]() векторів
векторів![]() ,
ортогональних до
,
ортогональних до![]() ,
утворює
,
утворює![]() вимірний
підпростір. Покажемо, що сукупність
вимірний
підпростір. Покажемо, що сукупність![]() інваріантний підпростір відносно
оператора
інваріантний підпростір відносно
оператора![]() .
Нехай
.
Нехай![]() .
Це означає, що
.
Це означає, що![]() .
Тоді
.
Тоді![]() ,
тобто
,
тобто![]() .
.
Дійсно,
![]() ,
де
,
де![]() – власне значення оператора
– власне значення оператора![]() ,
що відповідає власному вектору
,
що відповідає власному вектору![]() .
Теорему доведено.
.
Теорему доведено.
Теорема
5.
Для симетричного оператора
![]() існує ортогональний базис, в якому
матриця оператора
існує ортогональний базис, в якому
матриця оператора![]() діагональна і дійсна.
діагональна і дійсна.
Доведення.
За базис
![]() візьмемо попарно ортогональні власні
вектори
візьмемо попарно ортогональні власні
вектори![]() оператора
оператора![]() .
Тоді
.
Тоді![]() ,
тобто в цьому базисі матриця
,
тобто в цьому базисі матриця![]() оператора
оператора![]() має вигляд
має вигляд
 ,
,
де
![]() – дійсні числа.
– дійсні числа.
Навпаки,
нехай матриця оператора
![]() в ортогональному базисі має діагональний
вид. Для симетричного оператора відповідна
матриця одержується з матриці
в ортогональному базисі має діагональний
вид. Для симетричного оператора відповідна
матриця одержується з матриці![]() транспонуванням. Оскільки транспонування
не порушує діагональності матриці, то
одержуємо в результаті симетричну
матрицю, яка відповідає симетричному
оператору
транспонуванням. Оскільки транспонування
не порушує діагональності матриці, то
одержуємо в результаті симетричну
матрицю, яка відповідає симетричному
оператору![]() .
Теорему доведено.
.
Теорему доведено.
Теорема
6.
Для будь-якої симетричної матриці
![]() можна знайти таку ортогональну матрицю
можна знайти таку ортогональну матрицю![]() ,
яка зводить матрицю
,
яка зводить матрицю![]() до діагонального виду, тобто матриця
до діагонального виду, тобто матриця![]() ,
одержана трансформуванням матриці
,
одержана трансформуванням матриці![]() матрицею
матрицею![]() ,
буде діагональною.
,
буде діагональною.
Доведення.
Нехай
![]() – симетрична матриця
– симетрична матриця![]() ого
порядку,
ого
порядку,![]() – деякий ортонормований базис простору
– деякий ортонормований базис простору![]() .
Тоді матриця
.
Тоді матриця![]() задає в цьому базисі деякий симетричний
оператор
задає в цьому базисі деякий симетричний
оператор![]() .
В
.
В![]() існує ортонормований базис
існує ортонормований базис![]() ,
складений із власних векторів оператора
,
складений із власних векторів оператора![]() .
В цьому базисі
.
В цьому базисі![]() задається діагональною матрицею
задається діагональною матрицею![]() .
Тоді
.
Тоді
![]() ,
,
де
![]() – матриця переходу від базису
– матриця переходу від базису![]() до
до![]() ,
,
![]() .
.
Ця матриця, як матриця переходу від одного ортонормованого базису до іншого такого ж базису, буде ортогональною. Теорему доведено.
Оскільки
для ортогональної матриці
![]() її обернена матриця дорівнює транспонованій
її обернена матриця дорівнює транспонованій![]() ,
то рівність
,
то рівність![]() можна записати так
можна записати так![]() .
.
