
- •4 Лінійні та евклідові простори
- •4.1 Лінійні простори
- •4.2 Дійсний евклідовий простір
- •4.3 Ортонормований базис в евклідовому просторі
- •4.4 Ортогональне доповнення підпростору евклідового простору. Ізоморфізм евклідових просторів
- •4.5 Комплексний евклідовий (унітарний) простір
- •Приклади розв’язування задач
- •Тест для самоконтролю
- •Завдання для самостійного розв’язування
4.4 Ортогональне доповнення підпростору евклідового простору. Ізоморфізм евклідових просторів
Нехай
![]() – який-небудь підпростір евклідового
простору
– який-небудь підпростір евклідового
простору![]() .
Множина
.
Множина![]() всіх векторів
всіх векторів![]() простору
простору![]() ,
ортогональних кожному вектору
,
ортогональних кожному вектору![]() підпростору
підпростору![]() ,
називається ортогональним доповненням
підпростору
,
називається ортогональним доповненням
підпростору![]() відносно простору
відносно простору![]() .
Покажемо, що множина
.
Покажемо, що множина![]() є підпростором простору
є підпростором простору![]() .
Для цього потрібно переконається, що
сума двох будь-яких векторів множини
.
Для цього потрібно переконається, що
сума двох будь-яких векторів множини![]() належить цій множині і що добуток
будь-якого вектору множини
належить цій множині і що добуток
будь-якого вектору множини![]() на довільне дійсне число також належить
множині
на довільне дійсне число також належить
множині![]() .
Нехай
.
Нехай![]() і
і![]() – два довільні вектори множини
– два довільні вектори множини![]() ,
а
,
а![]() – який-небудь вектор підпростору
– який-небудь вектор підпростору![]() .
Очевидно,
.
Очевидно,![]() і
і![]() за властивыстю векторів множини
за властивыстю векторів множини![]() .
Так як
.
Так як![]() ,
то
,
то![]()
![]() .
Для довільного числа
.
Для довільного числа![]() маємо
маємо![]() .
Отже і вектор
.
Отже і вектор![]()
![]() .
Таким чином, множина
.
Таким чином, множина![]() є підпростором евклідового простору
є підпростором евклідового простору![]() .
.
З'ясуємо,
чи існують взагалі спільні вектори
підпросторів
![]() та
та![]() .
Нехай
.
Нехай![]() і
і![]() ,
тоді
,
тоді![]() ,
тобто
,
тобто![]() .
Отже, підпростори
.
Отже, підпростори![]() і
і![]() не мають спільних векторів, окрім вектора
не мають спільних векторів, окрім вектора![]() простору
простору![]() .
Звідси витікає, що сума цих підпросторів
є прямою.
.
Звідси витікає, що сума цих підпросторів
є прямою.
Евклідові
простори
![]() і
і![]() називаються ізоморфними, якщо між
векторами цих просторів можна встановити
таку взаємно-однозначну відповідність,
що
називаються ізоморфними, якщо між
векторами цих просторів можна встановити
таку взаємно-однозначну відповідність,
що![]() ,
,![]() ,
де
,
де![]() – образи векторів
– образи векторів![]() і
і![]() простору
простору![]() .
.
Теорема. Всі евклідові простори однієї розмірності ізоморфні.
4.5 Комплексний евклідовий (унітарний) простір
Лінійний
простір над полем комплексних чисел
називається комплексним евклідовим
простором або унітарним, якщо в ньому
визначена операція скалярного добутку
двох будь-яких векторів, тобто вказано
правило, за яким кожній парі векторів
![]() і
і![]() простору ставиться у відповідність
комплексне число
простору ставиться у відповідність
комплексне число![]() ,
при цьому виконуються наступні умови
(аксіоми скалярного добутку)
,
при цьому виконуються наступні умови
(аксіоми скалярного добутку)
1.
![]() ,
,![]()
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() .
.
Тут
![]() – довільне комплексне число,
– довільне комплексне число,![]() – число, спряжене числу
– число, спряжене числу![]() .
.
Комплексний
евклідовий простір можна зробити
нормованим, якщо кожному вектору
![]() поставити у відповідність дійсне число
поставити у відповідність дійсне число![]() .
Перевірка аксіом норми здійснюється
так само, як і в дійсному евклідовому
просторі. Вона основана на використанні
нерівності Коші – Буняковського для
унітарного простору
.
Перевірка аксіом норми здійснюється
так само, як і в дійсному евклідовому
просторі. Вона основана на використанні
нерівності Коші – Буняковського для
унітарного простору![]() .
.
В
унітарному просторі поняття кута між
двома векторами не використовується,
але два вектори
![]() і
і![]() такі, що
такі, що![]() ,
називаються ортогональними.
,
називаються ортогональними.
В комплексному евклідовому просторі існують ортонормовані базиси. Процес ортогоналізації довільного базису унітарного простору співпадає з процесом ортогоналізації базису дійсного евклідового простору.
Нехай
![]() – ортонормований базис комплексного
евклідового простору, а
– ортонормований базис комплексного
евклідового простору, а![]()
![]() і
і![]() – два довільно взятих вектори цього
простору. Тоді на основі аксіом і
властивостей скалярного добутку
– два довільно взятих вектори цього
простору. Тоді на основі аксіом і
властивостей скалярного добутку
![]()
де
![]() – числа, спряжені комплексним числам
– числа, спряжені комплексним числам![]() .
Таким чином
.
Таким чином![]() ,
тобто скалярний добуток двох векторів
унітарного простору, в якому вибраний
ортонормований базис, дорівнює сумі
добутків координат першого вектору на
відповідні спряжені значення координат
іншого вектору.
,
тобто скалярний добуток двох векторів
унітарного простору, в якому вибраний
ортонормований базис, дорівнює сумі
добутків координат першого вектору на
відповідні спряжені значення координат
іншого вектору.
Приклади розв’язування задач
Застосовуючи процес ортогоналізації, побудуйте ортогональний базис підпростору, натягнутого на дану систему векторів:
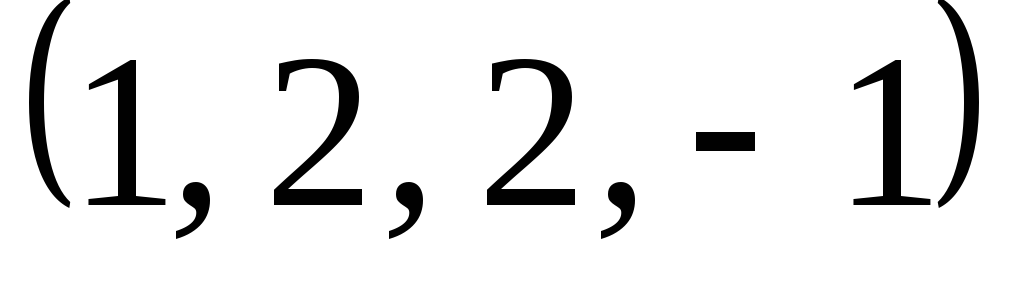 ,
, ,
, .
.
Розв’язання:
Складемо матрицю з координат векторів та зведемо її до ступінчатого виду методом елементарних перетворень рядків:
 .
.
![]() ,
,
![]() – кількість векторів, 3=
– кількість векторів, 3=![]()
![]() вектори лінійно незалежні.
вектори лінійно незалежні.
Нехай
![]() ,
тоді
,
тоді![]() .
.
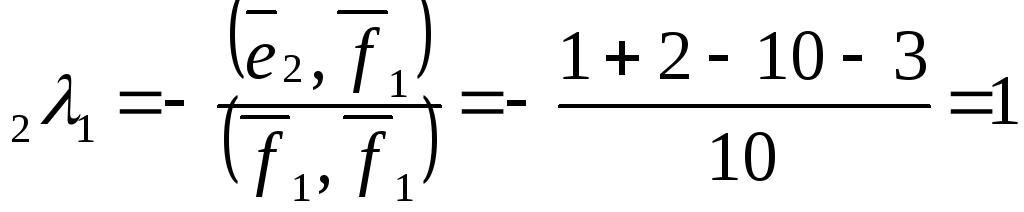 ,
,
![]() ,
,
![]() ,
,
 ,
,
 ,
,
![]() .
.
Перевіримо ортогональність знайдених векторів:
![]() ;
;
![]() ;
;
![]() .
.
Нормуємо
вектори:
![]() ;
;![]() ;
;![]() .
Тоді покладемо:
.
Тоді покладемо:
![]() ;
;
![]() ;
;
![]() ;
;
![]() –
–
– шуканий ортонормований базис.
Знайдіть ортогональну проекцію
 і ортогональну складову
і ортогональну складову вектора
вектора на лінійний простір
на лінійний простір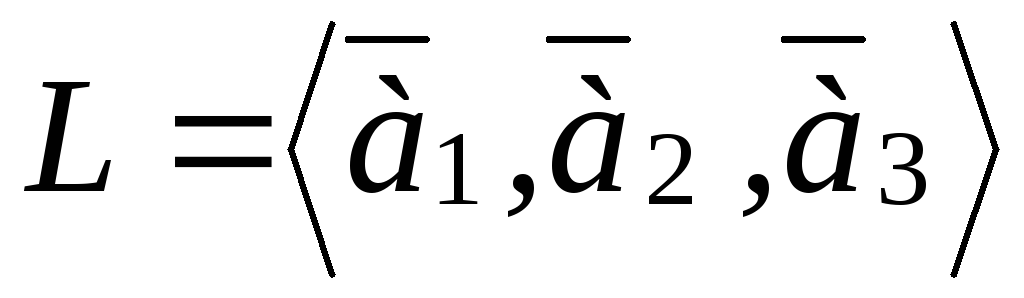 ,
де
,
де .
.
Розв’язання:
Перевіримо задані вектори на лінійну залежність. Для цього знайдемо ранг матриці, складеної з координат векторів:
 .
.
Так як
ранг матриці дорівнює 2, то
![]() .
.
Будемо
шукати ортогональну проекцію вектора
![]() на
на![]() у вигляді:
у вигляді:![]() .
Так як
.
Так як![]() – ортогональна складова, то
– ортогональна складова, то![]() =
=![]() +
+![]() =
=![]() .
Оскільки
.
Оскільки![]() ,
то:
,
то:
![]()
![]() ,
,
![]() .
.
Розв’яжемо
систему рівнянь
 за правилом Крамера:
за правилом Крамера:
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
Тоді
![]() ,
,![]() ,
,![]() .
.
Знайдіть базис ортогонального доповнення
 підпростору
підпростору ,
натягнутого на вектори
,
натягнутого на вектори ,
, ,
, .
.
Розв’язання:
Складемо матрицю з векторів для перевірки їх лінійної незалежності:
 .
.
Так як
![]() ,
то вектори
,
то вектори![]() лінійно залежні, незалежними будуть
вектори
лінійно залежні, незалежними будуть
вектори![]() .
.
Нехай
![]() належить ортогональному доповненню
належить ортогональному доповненню![]() підпростору
підпростору![]() .
Тоді він ортогональний до векторів
.
Тоді він ортогональний до векторів![]() ,
тобто
,
тобто![]() і
і![]() .
За цих умов складемо та розв’яжемо
систему рівнянь:
.
За цих умов складемо та розв’яжемо
систему рівнянь:

![]()

Складаємо таблицю для визначення ФСР:
-




–1
–2
2
0
–2
–1
0
1
Звідси
![]() і
і![]() ,
тобто
,
тобто![]() .
.
Доведіть, що скалярний добуток може бути заданий формулою
 .
.
Розв’язання:
Для доведення необхідно перевірити аксіоми скалярного добутку. Значення скалярного добутку є дійсним числом. Тоді
1.
![]() ;
;
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.

Так як
всі аксіоми виконуються, то
![]() визначає скалярний добуток.
визначає скалярний добуток.
Нехай дано два вектори
 .
Знайдіть довжини векторів
.
Знайдіть довжини векторів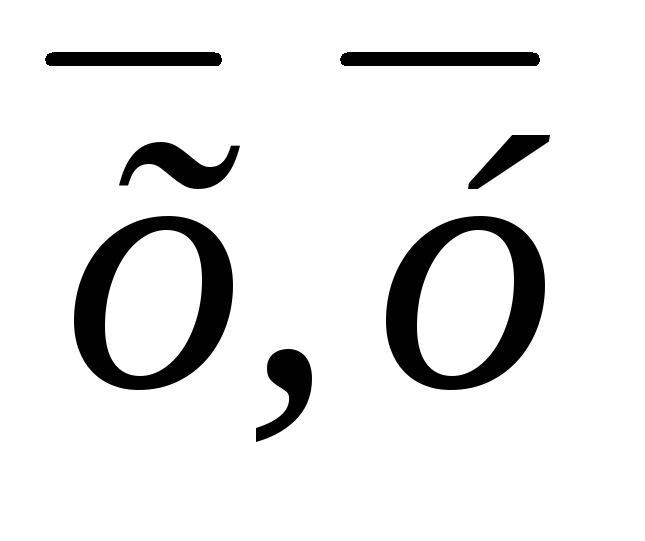 та
та ,
якщо:
,
якщо:
1.
![]() ;
2.
;
2.![]() .
.
Розв’язання:
1.
Скалярний добуток
![]()
![]() .
Довжина вектора визначається за формулою
.
Довжина вектора визначається за формулою![]() .
Тоді
.
Тоді![]() ,
,![]() .
Знайдемо
.
Знайдемо![]() :
:![]() .
.
2.
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Обчислимо
![]()
![]()
![]() .
.
Знайдіть норму вектора
 .
.
Розв’язання:
Для
того, щоб нормувати вектор, потрібно
знайти його довжину , а потім використати
формулу
![]() .
Отже,
.
Отже,![]() ,
,![]() .
.
