4 Лінійні та евклідові простори

4.1 Лінійні простори

В таких алгебраїчних структурах, як група, кільце, поле об’єктом розгляду є одна множина елементів, над якими можна проводити одну або дві алгебраїчні операції. Лінійний простір є алгебраїчною структурою, в якій фігурують дві множини: поле та адитивна абелева група. Для зручності елементи групи будемо називати векторами та позначати:Елементи полябудемо називати числами та позначати:

Множина називається лінійним простором над полем, якщо виконуються наступні умови:

I. множина є адитивною абелевою групою:

1. ,

2. ,

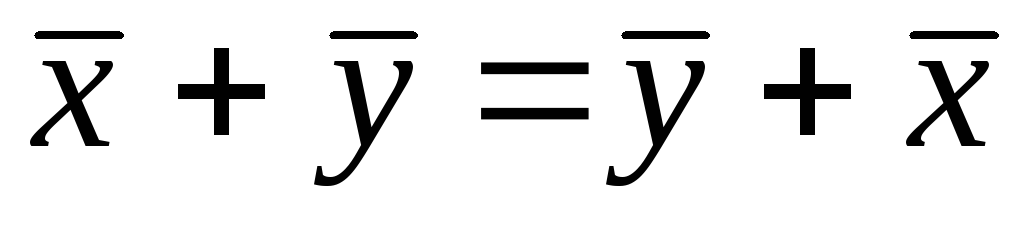3. існує нейтральний елемент ,

4. ;

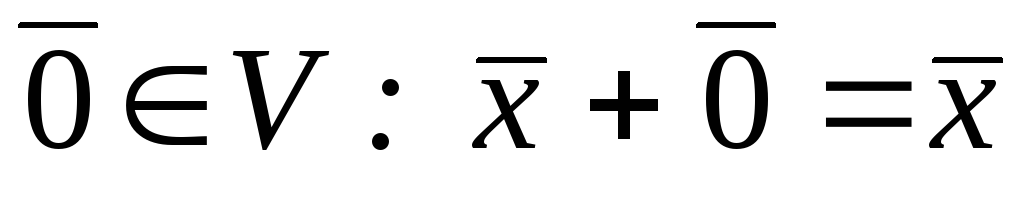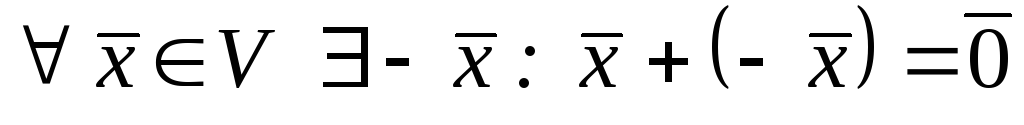II. кожній парі елементів іставиться у відповідність елемент:

1. ,

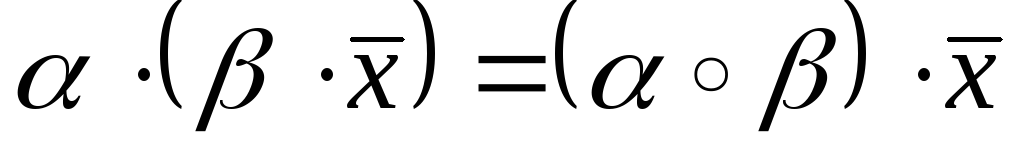2. , де – нейтральний елемент поля;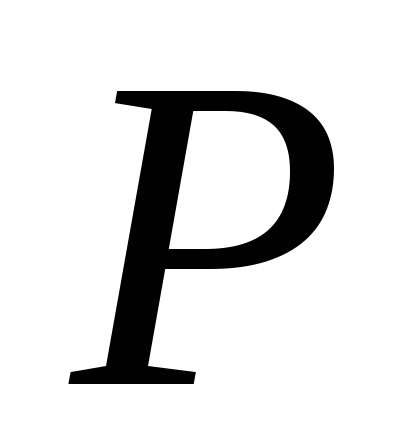

III. операції підпорядковуються законам дистрибутивності:

1. ,

2. .

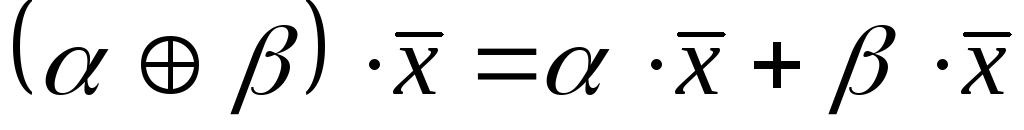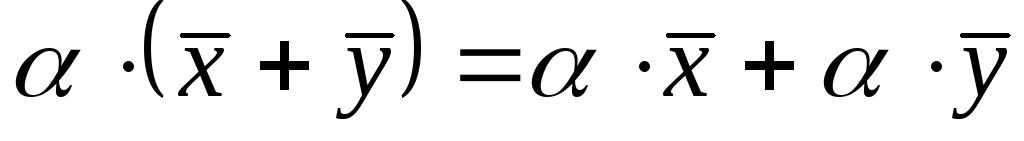При застосуванні теорії лінійних просторів найчастіше використовуються лінійні простори над полем дійсних або комплексних чисел. Тому в подальшому під полем будемо розуміти одне зі вказаних полів.

Два лінійних простори інад одним полемназиваються ізоморфними, якщо між векторами цих просторів можна встановити таку взаємно однозначну відповідність, що сумі векторів просторувідповідає сума їх образів зта векторупросторувідповідає векторз, тобто.

Вектори лінійного просторуназиваються лінійно залежними, якщо існують такі числаз поля, серед яких не всі дорівнюють нулю, що. Якщо остання рівність можлива лише у випадку, коли, то векториназиваються лінійно незалежними.

Лінійний простір над полемназиваються скінчено вимірним, якщо у ньому можна знайти скінчену максимальну лінійно незалежну систему векторів. Всяка така система називається базою (базисом) простору. Кількість векторів бази називається розмірністю простору.

Нехай вектори є базою скінчено вимірного просторунад полем дійсних або комплексних чисел. Тоді довільний векторпростору можна представити у вигляді лінійної комбінації векторів бази:. Числаназиваються координатами векторав базі.

Теорема 4.1. Якщо лінійні простори танад полемізоморфні, то лінійно незалежній системі векторівпросторувідповідає лінійно незалежна система їх образівпростору.

Наслідок. Якщо простори таізоморфні, то образом бази одного простору є база другого простору.

Нехай та– дві різні бази одного- вимірного лінійного простору(над полем дійсних або комплексних чисел). Для зручності назвемо базустарою, ановою. Представимо кожний вектор нової бази у вигляді комбінації векторів старої:

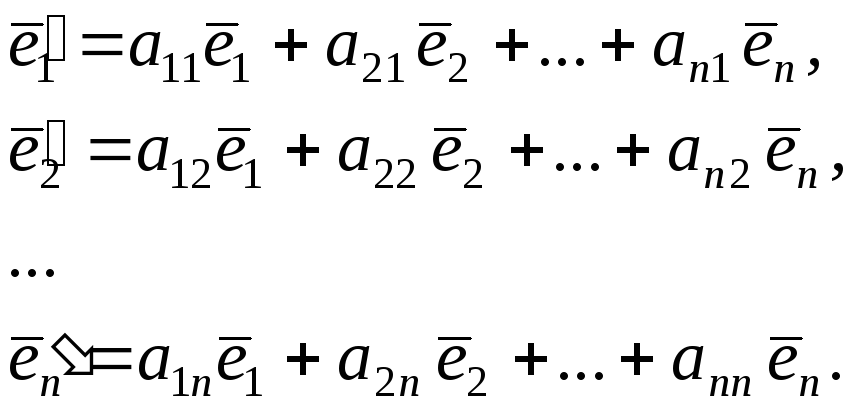(4.1.

Матрицю координат векторів нового базису у старому базисі

будемо називати матрицею переходу від старої бази до нової.

Введемо у розгляд матриці-стовпці

та .

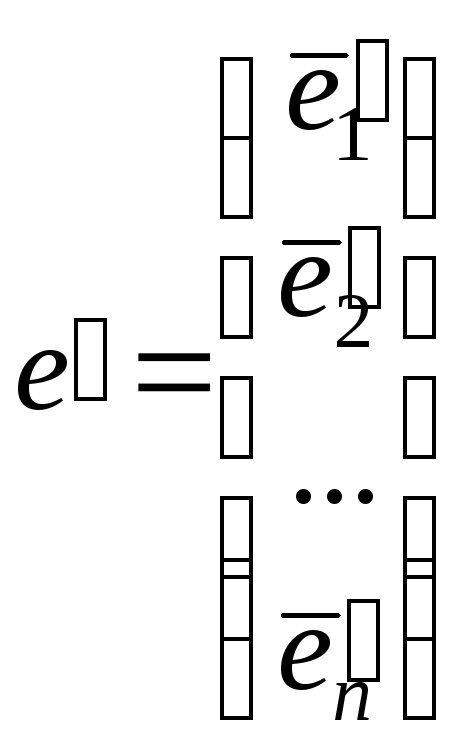Тоді за допомогою цих матриць систему (4.1. можна записати у вигляді: . Зауважимо, що матрицяневироджена.

Нехай вектор задано своїми координатами у старому базисі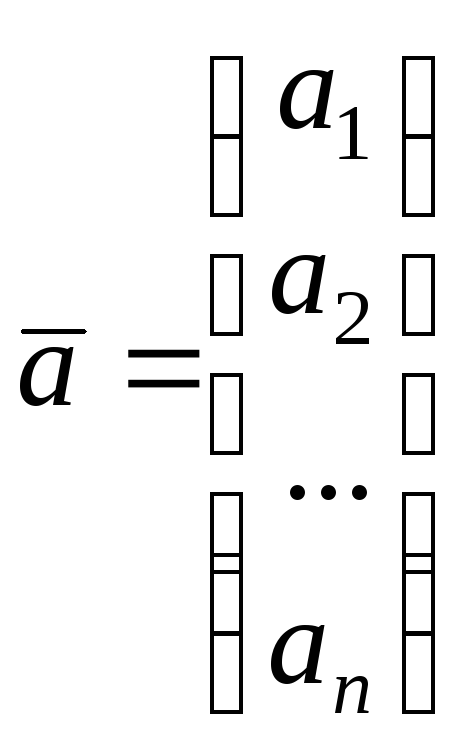. Тоді його координати у новому базисі можна визначити за формулою:.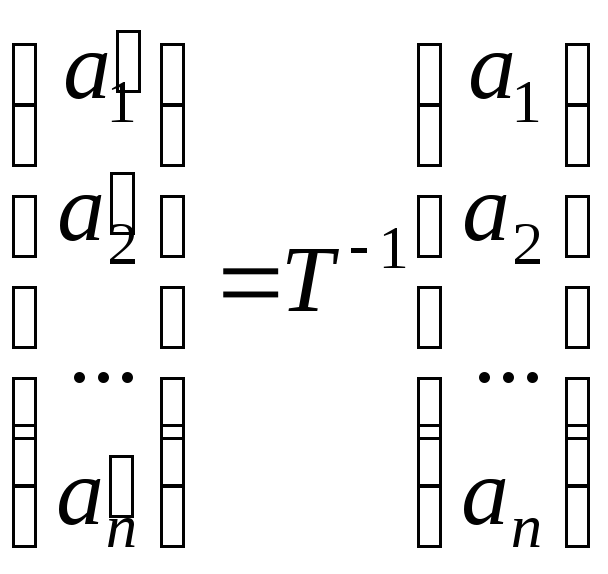

Множина лінійного векторного просторунад полемдійсних або комплексних чисел називається підпростором простору, якщо. Довільна максимальна лінійно незалежна сукупність векторів підпросторуназивається базою підпростору, а число векторів, що входять до бази, називається розмірністю підпростору.

Нехай – множина векторівлінійного простору. Сукупність всіх можливих комбінацій цих векторів, кожна з яких складається зі скінченої кількості векторів множини, називається оболонкою множинита позначається. Лінійна оболонкає підпростором простору.

Теорема 4.2. Нехай множина складається зі скінченого числа векторівлінійного простору, тоді розмірність оболонкидорівнює рангу системи векторів.

Нехай – скінчено вимірний лінійний простір над полем дійсних або комплексних чисел, ата– два підпростори цього простору. Сумоюназивають лінійну оболонку їх об’єднання. Так як оболонка довільної множини векторів просторує підпростором простору, то сума підпросторівтає деяким підпростором простору. Перетином двох підпросторівтапросторуназивають таку множину векторів, кожний з яких належить одночасно і підпросторуі підпростору. Перетиндвох підпросторівтатакож є підпростором простору.

Теорема 4.3. Нехай та– два підпростори лінійного простору. Тоді.

Наслідок. Якщо підпростори та-вимірного просторутакі, що, то підпростірмістить хоча б один ненульовий вектор.

Якщо підпростір містить лише нульовий вектор, то сума таких підпросторів називається прямою та позначається.

Теорема 4.4. Нехай та– підпростори лінійного простору, причому. Тоді довільний вектор просторуможна представити єдиним чином у вигляді суми двох векторів, один з яких належить підпростору, а другий –.

Теорема 4.5. Якщо -вимірний лінійний простіррозкладається у пряму суму підпросторівта, тобто, то.

Нехай та– два підпростори лінійного простору, причому. Якщо існує такий підпростірпростору, що, то підпростірназивають прямим доповненням до підпросторувідносно підпростору.

Теорема 4.6. Якщо та– два підпростори лінійного простору, причому, то існує підпростірпростору, що є прямим доповненням до підпросторувідносно підпростору.